Proof
Proof Revision
Proof
The idea of a proof is to make a universal statement – for example, you don’t just want to say that the angles in some triangles add up to 180\degree, you want to say that the angles in all triangles add up to 180\degree. This is a proof you actually do have to know, and you can see it here ( interior and exterior angles revision )
There are 6 classic proof questions types you may have to face.
Having a good understanding of the following topics will help with proof:
Take Note
Students often think you can’t teach or learn how to do proof questions as they are all different, but they do often use the same logic. The following logic will help with different algebraic proofs questions:
- n is a number so 2n must always be even
- 2n+1 must therefore always be odd
Note: Factorising and expanding brackets can often help to identify rules so keep this in mind.
Algebraic Arguments
We can use the odd and even properties outlined above to prove or disprove rules or arguments.
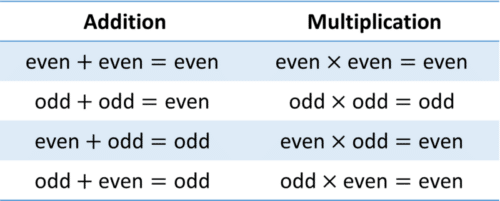
Even though a proposed rule may be true for certain examples, a mathematical proof is needed to show that the rule holds in all cases. Only one counter-example (an example where the rule isn’t true) is needed to disprove the rule.
Example:
If n is an odd number, show that (n+2)\times (n+5) is always even.
If n is odd, then (n+2) will be odd and (n+5) will be even.
So (n+2)\times (n+5) is even, because odd \times even = even
Example:
Laura says, “Every prime number is also an odd number”.
Find a counter-example to disprove Laura’s statement.
2 is a prime number, however it is even, hence Laura’s statement is false.
Type 1: Disproof by Counterexample
Disproof by counter example is a way of disproving a statement by providing one example which doesn’t work for the statement.
Example: Hernan claims “if you square a number and add 1, the result is a prime number”. Find a counterexample to prove her statement wrong.
To make life easy, we’ll start with the smaller numbers.
1^2+1=1+1=2,\text{ which is prime.}
2^2+1=4+1=5,\text{ which is prime.}
Now, at this point it might seem like her statement is true, but if we try the next square number:
3^2+1=9+1=10,\text{ which is not prime.}
This is a counterexample for her statement, so we have proved it to be false.
Type 2: Algebraic Equivalent
Algebraic equivalent proofs will present you with a two sided equation, usually with a \equiv rather then an =. The task is to play around with one side until it looks like the other.
Example: 3(n + 3)(n − 1)− 3(1− n) \equiv (3n − 3)(n + 4)
Here we need to expand out all the brackets and collect the resulting like terms.
\begin{aligned}3(n + 3)(n − 1)− 3(1− n) &\equiv (3n − 3)(n + 4) \\ 3(n^2+2n-3)-3+3n &\equiv 3n^2 +12n-3n-12 \\ 3n^2 +6n-9-3+3n &\equiv 3n^2 +12n-3n-12\\ 3n^2 +9n-12 &\equiv 3n^2 +9n-12 \end{aligned}
We can see now that the two sides of the equation are equivalent (\equiv)
Type 3: Geometric Proof
Geometric proofs involve proving something fundamental about a shape, often these are things you know to be true already you just need to prove it.
Example: Prove that the sum of the interior angles of a triangle add up to 180\degree
Here we can see a triangle with the angles \textcolor{red}{a}, \textcolor{limegreen}{b} and \textcolor{blue}{c}
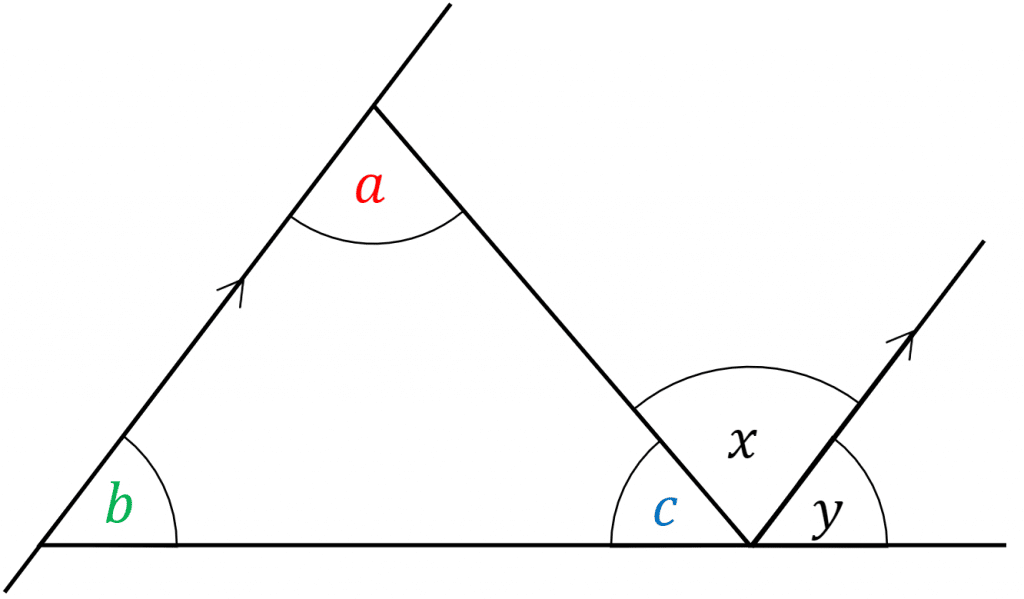

We know;
\textcolor{limegreen}{b} = \textcolor{black}{y} (Corresponding angle)
\textcolor{red}{a} = \textcolor{black}{x} (Alternate angles)
\textcolor{blue}{c} + \textcolor{black}{x} + \textcolor{black}{y} = 180\degree
This means,
\textcolor{red}{a} + \textcolor{limegreen}{b} + \textcolor{blue}{c} = 180\degree
So in these four lines we have proved the angles in a triangle add up to 180\degree
Type 4: Algebraic Proof
Algebraic proofs involve constructing an algebraic expression to match the statement, then proving or disproving the statement with this expression.
When constructing algebraic proof, we can associate common statements with their equivalent algebraic expressions.
The list below summarises statements that frequently occur.
- Even numbers \rightarrow 2n
- Odd numbers \rightarrow 2n+1
- Consecutive numbers \rightarrow n \text{ and } n+1
- Consecutive even numbers \rightarrow 2n \text{ and } 2n+2
- Consecutive odd numbers \rightarrow 2n+1 \text{ and } 2n+3
- Proving a statement is always positive or a square number – the expression would need to be simplified to (...)^2
- Proving a statement is a multiple of x or divisible by x – the expression would need to be factorised to the form x(...)
This topic can get very challenging, but a simple example is shown below.
Example: Prove algebraically that the sum of two consecutive numbers is odd.
Step 1: Form the algebraic expression.
We know a number can be represented by n, so the next number would be (n+1).
n + (n+1)
Step 2: Expand / simplify the expression as much as possible.
n + n+1 = 2n+1
Step 3: Use the expression to prove the statement.
For this example, this is easy as the expression is already in the correct format.
2n+1 = Odd number
Type 5: Proofs with indices
Questions involving indices will require a good knowledge of your indices rules.
Example: Prove that the difference between 24^{12} and 15^{10} is a multiple of 3
Step 1: Write the expression to find the difference
24^{12}- 15^{10}
Step 2: Take a out a factor of 3 from each term.
\begin{aligned}(24\times24^{11}) &- (15\times15^9) \\ (3\times8\times24^{11}) &- (3\times5\times15^9)\end{aligned}
Step 3: Factorise by 3
(3\times8\times24^{11}) - (3\times5\times15^9) = 3([8\times24^{11}] - [5\times15^9])
We know that 3\times(\text{any integer}) is a multiple of 3 therefore,
3([8\times24^{11}] - [5\times15^9]) is a multiple of 3
Type 6: Proofs with Primes
A common question involves proving that an expression isn’t prime.
Example: Show that 5^{89} - 401 is not a prime number.
We know Odd \times Odd = Odd, therefore,
5^{89} is Odd
We know Odd - Odd=Even
5^{89} - 401 = Even
Even numbers cannot be prime.
Example 1: Algebraic Proof
Prove that the square of an odd number is also odd.
[3 marks]
Step 1: Form the algebraic expression.
We know that an odd number can be represented by 2n+1, which needs to be squared.
(2n+1)^2
Step 2: Expand and simplify the expression as much as possible.
\begin{aligned}(2n+1)^2 &= 4n^2+2n+2n+1 \\ &= 4n^2+4n+1\end{aligned}
Step 3: Use the expression to prove the statement.
How do we know this is odd? Well, we can take a factor of 2 out,
2(2n^2+2n)+1
We know 2x+1 is an odd number so..
2(2n^2+2n)+1
is just
2\times(\text{some whole number})+1.
Example 2: Algebraic proof
Example: Prove that (n+2)^2-(n-2)^2 is divisible by 8 for any positive whole number n.
[2 marks]
Step 1: Expand and simplify the expression
\begin{aligned}(n+2)^2&-(n-2)^2 \\ (n^2+4n+4) &- (n^2-4n+4)\end{aligned}
We can see that the n^2 terms will cancel, as will the 4s, so all we’re left with is
(n^2+4n+4)-(n^2-4n+4)=4n-(-4n)=8n
So, the whole expression simplifies to
8n
Step 2: Factorise the expression
8n = 8(n)
Now, if n is a whole number, then 8(n) must be divisible by 8. Thus, we have completed the proof.
Proof Example Questions
Question 1: Luke claims that if you square an even number and add 3, the answer is prime. Find a counterexample to show that Luke’s statement is false.
[2 marks]
We will try the first few even numbers (squaring them and adding 3) until we find an example that isn’t prime. So, we get
2^2+3=4+3=7,\text{ which is prime}.
4^2+3=16+3=19,\text{ which is prime}.
6^2+3=36+3=39,\text{ which is not prime}.
Since 39 is divisible by 3, it must not be prime, so we have proved Luke’s statement to be false.
Note: there are many counter examples to Luke’s statement, and any one of them is an acceptable answer to this question.
Question 2: Show that the following identity is true,
\begin{aligned}5(3x-5)-2(2x+9)\equiv11x-43\end{aligned}
[2 marks]
To show that the left and right hand sides of the equation are identical we expand the brackets on the left hand side,
5(3x-5)-2(2x+9) = 15x-25-4x-18 \\ = 11x-43
Hence we have show the identity is true.
Question 3: Prove that (3n+1)^2+(n-1)^2 is always even for any positive whole number n.
[3 marks]
To answer this question, we will need to expand and simplify the expression given to us, so we can hopefully write it in a way that shows it is clearly divisible by 2 (since that’s the definition of even). So, expanding the first bracket, we get
(3n+1)^2=9n^2+3n+3n+1=9n^2+6n+1.
Then, expanding the second bracket, we get
(n-1)^2=n^2-n-n+1=n^2-2n+1.
Adding the expansions together, we get
(9n^2+6n+1)+(n^2-2n+1)=10n^2+4n+2
Is this an even number? Well, if we take a factor of 2 out of the expression:
2(5n^2+2n+1),
we see that since 5n^2+2n+1 is a whole number because n is a whole number, the expression in question is equal to 2\times(\text{some whole number}) and so must be even. Thus, we have completed the proof.
Question 4: Prove that the sum of 3 consecutive odd numbers is an odd number.
[2 marks]
For any 3 consecutive odd numbers: 2n+1, 2n+3, and 2n+5, adding them together gives us,
(2n+1)+(2n+3)+(2n+5)=6n+9
Now, to show that this number is odd we write this expression instead like 6n+8+1, then we get
6n+8+1=2(3n+4)+1
Since n is a whole number, clearly 3n+4 must also be a whole number, so we get that our expression is of the form 2\times\text{(some whole number)}+1, which is an odd number and so the result must be odd. Thus, we have completed the proof.
Question 5: Show algebraically that the sum of any 3 consecutive even numbers is always a divisible by 6.
[3 marks]
For any 3 consecutive even numbers: 2n, (2n+2) and (2n+4), adding them together gives us,
2n+(2n+2)+(2n+4)=6n+6
Now, to show that this number is divisible by 6 we simply take out a factor of 6, then we get
2n+(2n+2)+(2n+4)=6(n+1)
For any 3 consecutive even numbers: 2n, (2n+2) and (2n+4), adding them together gives us,
2n+(2n+2)+(2n+4)=6n+6
Now, to show that this number is divisible by 6 we simply take out a factor of 6, then we get
2n+(2n+2)+(2n+4)=6(n+1)





