Revise
Interior and Exterior Angles
Interior and Exterior Angles Revision
Interior and Exterior Angles
The interior angles of a shape are the angles inside the shape.
The exterior angles are the angles formed between a side-length and an extension.
Rule: Interior and exterior angles add up to 180\degree.
Having the ability to rearrange equations will help with interior and exterior angle questions.
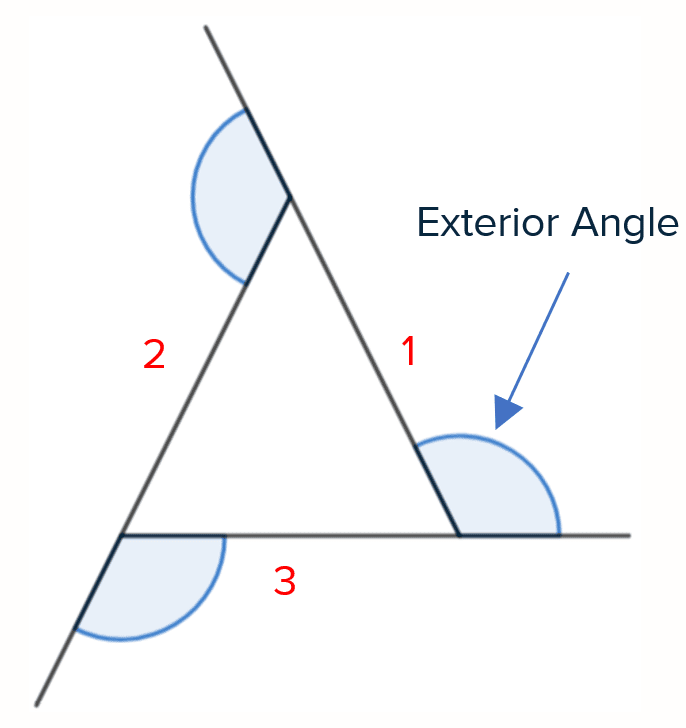
Exterior Angles
Rule: The exterior angle = \dfrac{360\degree}{\textcolor{red}{n}}
where \textcolor{red}{n} is the number of sides.
The sum of all the exterior angles will equal 360\degree.
For the triangle shown, we can see it has \textcolor{red}{3} sides, so to calculate an exterior angle we do:
\dfrac{360\degree}{\textcolor{red}{3}} = 120\degree
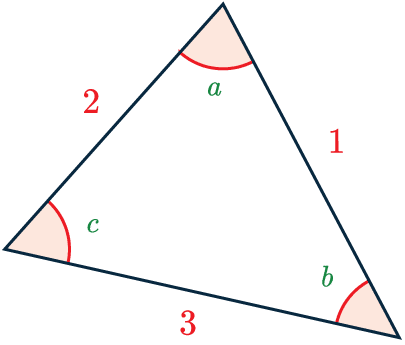
Interior Angles
Rule: Sum of interior angles = (\textcolor{red}{n} - 2) \times 180\degree
Where \textcolor{red}{n} is the number of sides.
To find the sum of the interior angles for the triangle shown we do the following:
(\textcolor{red}{3} - 2) \times 180\degree = 180\degree
This means that
\textcolor{limegreen}{a} + \textcolor{limegreen}{b} + \textcolor{limegreen}{c} = 180\degree
Note: You can find the interior angle of a regular polygon by dividing the sum of the angles by the number of angles. You can also find the exterior angle first then minus from 180\degree to get the interior angle.
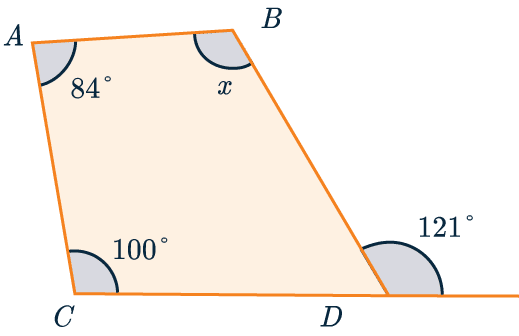
Example: Finding Interior and Exterior Angles
ABCD is a quadrilateral.
Find the missing angle marked x.
[2 marks]
This is a 4-sided shape, to work out the interior angles we calculate the following:
(\textcolor{red}{n}-2)\times 180 =360\degree.
Next we can work out the size of \angle CDB as angles on a straight line add up to 180\degree.
180 - 121 = 59\degree
Now we know the other 3 interior angles, we get that
x = 360 - 84 - 100 - 59 = 117\degree
Interior and Exterior Angles Example Questions
Question 1: The shape below is a regular pentagon.
Work out the size of the interior angle, x.
[2 marks]
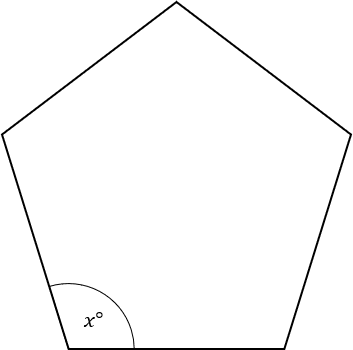
This shape has 5 sides, so its interior angles add up to,
180 \times (5 - 2) = 540\degree
Hence each interior angle is,
x\degree=540\degree \div 5 = 108\degree
Question 2: The shape below is a regular octagon.
Work out the size of the interior angle, x.
[2 marks]
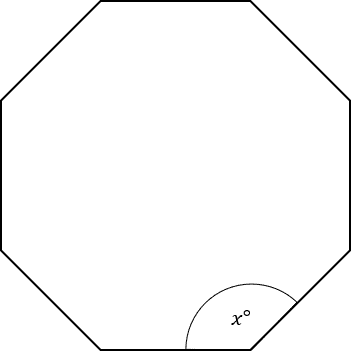
This shape has 8 sides, so its interior angles add up to,
180 \times (8 - 2) = 1080\degree
Hence each interior angle is,
x\degree=1080\degree \div 8 = 135\degree
Question 3: ABCDE is a pentagon.
Work out the size of x.
[3 marks]
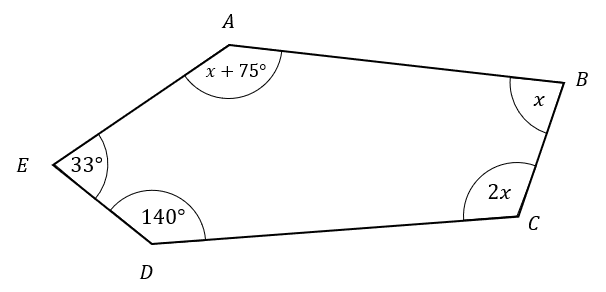
This shape has 5 sides, so its interior angles must add up to
180 \times (5 - 2) = 540\degree.
We can’t find this solution with one calculation as we did previously, but we can express the statement “the interior angles add up to 540” as an equation. This looks like
33 + 140 + 2x + x + (x + 75) = 540
Now, this is a linear equation we can solve. Collecting like terms on the left-hand side, we get
4x + 248 = 540.
Subtract 248 from both sides to get
4x = 292.
Finally, divide by 4 to get the answer:
x = 292 \div 4 = 73\degree
Question 4: ABCD is a quadrilateral.
Work out the size of y.
[4 marks]
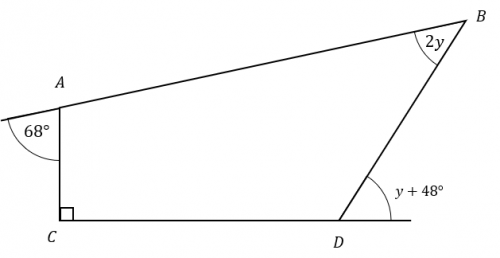
This shape has 4 sides, so its interior angles add up to
180 \times (4 - 2) = 360\degree.
We don’t have any way of expression two of the interior angles at the moment, but we do have their associated exterior angles, and we know that interior plus exterior equals 180. So, we get
\text{interior angle CDB } = 180 - (y + 48) = 132 - y
Furthermore, we get
\text{interior angle CAB } = 180 - 68 = 112
Now we have figures/expressions for each interior angle, so we write the sum of them equal to 360 in equation form:
112 + 90 + 2y + (132 - y) = 360
Collecting like terms on the left-hand side, we get
y + 334 = 360
Then, if we subtract 334 from both sides we get the answer to be
y = 360 - 334 = 26\degree.
Interior and Exterior Angles Worksheet and Example Questions
(NEW) Interior and Exterior Angles Exam Style Questions - MME
Level 4-5GCSENewOfficial MMEInterior and Exterior Angles Drill Questions
Interior angles of polygons
Level 4-5GCSE
