Stationary Points
Stationary Points Revision
Stationary Points
When \dfrac{df(x)}{dx}>0, the function f(x) is increasing.
When \dfrac{df(x)}{dx}<0, the function f(x) is decreasing.
A stationary point of a function is when it is neither increasing – i.e. when \dfrac{df(x)}{dx}=0
Make sure you are happy with the following topics before continuing.
Finding Stationary Points
To find a point where the gradient is 0, we need to set \dfrac{dy}{dx} = f'(x) = 0.
So, let’s say we’ve got a nice, easy function: \textcolor{blue}{y = x^2 - 1}.
Well, we know that the gradient is given by \dfrac{dy}{dx} = 2x.
Setting \textcolor{limegreen}{\dfrac{dy}{dx} = 2x = 0} gives x = 0, for which y = 0^2 - 1 = -1.
We conclude that \textcolor{blue}{y = x^2 - 1} has a stationary point at (0, -1).
Finding Stationary Points of Complicated Functions
Let \textcolor{blue}{y = \sin x + \cos x} for x measured in radians. How might we go about finding the stationary points (in the range
0 \leq x \leq 2\pi)?
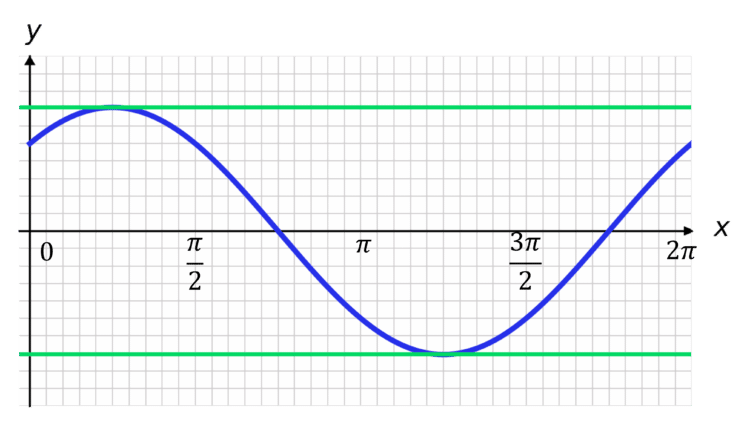
\textcolor{blue}{y = \sin x + \cos x} gives \dfrac{dy}{dx} = \cos x - \sin x.
Setting \textcolor{limegreen}{\dfrac{dy}{dx} = 0}, we require \cos x = \sin x, or, \tan x = 1.
This gives x = \tan ^{-1}(1) = \dfrac{\pi}{4}, \dfrac{5\pi}{4}.
Therefore, for 0 \leq x \leq 2\pi, we have the stationary points \left( \dfrac{\pi}{4}, \sqrt{2}\right) , \left( \dfrac{5\pi}{4}, -\sqrt{2}\right).
Finding the Nature of Stationary Points
Once we’ve found our stationary points, we need to find out whether they are a maximum, minimum, or a stationary point of inflection.
We do this by differentiating our derivative again.
So, for example, take our first example of y = x^2 - 1.
We said that \dfrac{dy}{dx} = 2x.
So \dfrac{d^{2}y}{dx^2} = 2.
Since \dfrac{d^{2}y}{dx^2} = 2 > 0, we can conclude that this is a minimum point. You probably figured that out from the graph, though.
What about the second example, y = \sin x + \cos x?
Well, we know that \dfrac{dy}{dx} = \cos x - \sin x.
By extension, \dfrac{d^{2}y}{dx^2} = -\sin x - \cos x. We now need to test both of our values of x for the corresponding value of \dfrac{d^{2}y}{dx^2}.
So, for x = \dfrac{\pi}{4}, \dfrac{d^{2}y}{dx^2} = -\sqrt{2} < 0, so it is a maximum point.
For x = \dfrac{5\pi}{4}, \dfrac{d^{2}y}{dx^2} = \sqrt{2} > 0, so it is a minimum point.
Note
\dfrac{d^{2}y}{dx^{2}}=0 doesn’t always mean the stationary point is a point of inflection.
For example, y=x^{4} has a minimum at x=0, but \dfrac{d^{2}y}{dx^{2}}=12x^{2}, which equals 0 at x=0, so in this case \dfrac{d^{2}y}{dx^{2}}=0 leads to a minimum.
However, all points of inflection have the property \dfrac{d^{2}y}{dx^{2}}=0, so to interpret the result \dfrac{d^{2}y}{dx^{2}}=0 you will need to check whether the second derivative changes sign either side of the stationary point.
Sketching Graphs from Information about Functions
Say we have a complex function with multiple terms, i.e. \textcolor{blue}{f(x) = 1 + x - 2\cos x} where -2\pi \leq x \leq 2\pi is measured in radians.
Then f'(x) = 1 + 2\sin x and f''(x) = 2\cos x.
Therefore, any stationary points will occur when \sin x = \dfrac{-1}{2}, so x = \dfrac{-5\pi}{6}, \dfrac{-\pi}{6}, \dfrac{7\pi}{6}, \dfrac{11\pi}{6}.
For x = \dfrac{-5\pi}{6}, f(x) = 0.114 and f''(x) = -\sqrt{3}, which is a maximum.
For x = \dfrac{-\pi}{6}, f(x) = -1.256 and f''(x) = \sqrt{3}, which is a minimum.
For x = \dfrac{7\pi}{6}, f(x) = 6.397 and f''(x) = -\sqrt{3}, which is a maximum.
For x = \dfrac{11\pi}{6}, f(x) = 5.028 and f''(x) = \sqrt{3}, which is a minimum.
We can sketch these parts onto a graph to give us a rough form.
We can be helped further in sketching by considering the behaviour of the graph as x gets really big or really small. We know that the graph roughly follows y=x+1, so as x gets really big so does y, and as x gets really small so does y. With this, we can finish our graph.
Stationary Points Example Questions
Question 1: Find the stationary point of f(x) = (x - 1)(x + 4).
[3 marks]
f(x) = x^2 + 3x - 4
gives
f'(x) = 2x + 3
f'(x) = 0 when x = -\dfrac{3}{2}.
Substituting this value into f(x) gives y=-\dfrac{25}{2}
Thus, the stationary point is at \bigg(-\dfrac{3}{2}, -\dfrac{25}{4}\bigg)
Question 2: Determine the nature of the stationary point for the function y = 9 - x^2.
[3 marks]
y = 9 - x^2 gives
\dfrac{dy}{dx} = -2x
leading to
\dfrac{d^2y}{dx^2} = -2
-2 < 0, so this is a maximum point.
Question 3: For the function f(x) = x^4 + \dfrac{8}{3}x^3 - 10x^2 - 24x, find the x-coordinates of the stationary points, and determine their nature.
[5 marks]
f(x) = x^4 + \dfrac{8}{3}x^3 - 10x^2 - 24x
f'(x) = 4x^3 + 8x^2 - 20x - 24
f'(x) = 4x^3 + 8x^2 - 20x - 24 = 0 can be simplified to x^3 + 2x^2 - 5x - 6 = 0
x^3 + 2x^2 - 5x - 6 = (x + 1)(x^2 + x - 6) = (x + 1)(x - 2)(x + 3) = 0
So, f'(x) = 0 has solutions at x = -3, -1, 2.
f''(x) = 12x^2 + 16x - 20
So
f''(x) = 40 > 0 when x = -3, so this is a minimum point.
f''(x) = -24 < 0 when x = -1, so this is a maximum point.
f''(x) = 60 > 0 when x = 2, so this is a minimum point.










