Revise
Differentiating Trig Functions
Differentiating Trig Functions Revision
Differentiating Trig Functions
We’re now going to look at how to differentiate the simple trig functions – that’s \textcolor{blue}{\sin}, \textcolor{limegreen}{\cos} and \textcolor{red}{\tan}.
Make sure you are happy with the following topics before continuing.
Simple Trig Results
Below is a diagram showing the derivative and integral of the basic trigonometric functions, \sin x and \cos x.
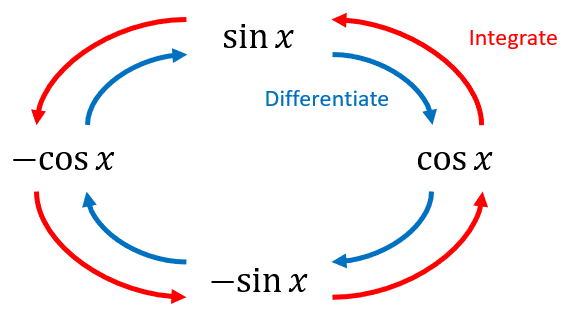
General Trig Differentiation
Below is a table of three derivative results.
Using the Chain Rule with Trig Functions
We can also use the Chain Rule to differentiate more complex trig functions.
For example, say we have f(x) = \textcolor{blue}{\sin} (x^2 - x + 1).
Then we can set \textcolor{red}{u} = x^2 - x + 1 and f(x) = g(\textcolor{red}{u}) = \textcolor{blue}{\sin} \textcolor{red}{u}.
Then \dfrac{d\textcolor{red}{u}}{dx} = 2x - 1 and \dfrac{df(x)}{d\textcolor{red}{u}} = \textcolor{limegreen}{\cos} u.
So,
\dfrac{df(x)}{dx} = (2x - 1)\textcolor{limegreen}{\cos} (x^2 - x + 1)
From First Principles
We can also find the derivatives from first principles.
For example, let f(x) = \textcolor{limegreen}{\cos} x. Then
f'(x) = \lim\limits_{\textcolor{purple}{h} \to 0}\left( \dfrac{\textcolor{limegreen}{\cos} (x + \textcolor{purple}{h}) - \textcolor{limegreen}{\cos} x}{\textcolor{purple}{h}} \right)
= \lim\limits_{\textcolor{purple}{h} \to 0}\left( \dfrac{\textcolor{limegreen}{\cos} x \textcolor{limegreen}{\cos} \textcolor{purple}{h} - \textcolor{blue}{\sin} x \textcolor{blue}{\sin} h - \textcolor{limegreen}{\cos} x}{\textcolor{purple}{h}}\right)
= \lim\limits_{\textcolor{purple}{h} \to 0}\left( \dfrac{\textcolor{limegreen}{\cos} x(\textcolor{limegreen}{\cos} \textcolor{purple}{h} - 1) - \textcolor{blue}{\sin} x \textcolor{blue}{\sin} \textcolor{purple}{h}}{\textcolor{purple}{h}}\right)
Using small angle approximations, we have
f'(x) = \lim\limits_{\textcolor{purple}{h} \to 0}\left( \dfrac{-\dfrac{1}{2}\textcolor{purple}{h}^2 \textcolor{limegreen}{\cos} x - \textcolor{purple}{h}\textcolor{blue}{\sin} x}{\textcolor{purple}{h}}\right)
= \lim\limits_{\textcolor{purple}{h} \to 0}\left( \dfrac{-1}{2}\textcolor{purple}{h}\textcolor{limegreen}{\cos} x - \textcolor{blue}{\sin} x\right)
= -\textcolor{blue}{\sin} x
Differentiating Trig Functions Example Questions
Question 1: Give an expression for \dfrac{dy}{dx} in terms of y, when x = \tan y.
[2 marks]
x = \tan y gives
\dfrac{dx}{dy} = \sec ^2 y
Then \dfrac{dy}{dx} = \cos ^2 y.
Question 2: For \tan x^2, find the derivative with respect to x.
[2 marks]
Let u = x^2 and y = \tan u.
Then
\dfrac{dy}{dx} = 2x \times \sec ^2 u = \dfrac{2x}{\cos ^2 x^2}
Question 3: Prove that the derivative of \sin kx is k\cos kx, using the first principles technique.
[4 marks]
f'(x) = \lim\limits_{h \to 0}\left( \dfrac{\sin (kx + kh) - \sin kx}{h} \right)
= \lim\limits_{h \to 0}\left( \dfrac{\sin kx \cos kh + \sin kh \cos kx - \sin kx}{h}\right)
= \lim\limits_{h \to 0}\left( \dfrac{\sin kx(\cos kh - 1) + \sin kh \cos kx}{h}\right)
Using small angle approximations, we have
f'(x) = \lim\limits_{h \to 0}\left( \dfrac{-\dfrac{1}{2}(kh)^2 \sin kx + kh\cos kx}{h}\right)
= \lim\limits_{h \to 0}\left( \dfrac{-1}{2}kh\sin kx + k\cos kx\right)
= k\cos kx
Differentiating Trig Functions Worksheet and Example Questions
Differentiation
A Level
