Reciprocal Trig Functions

Remember how we said that $\sin ^{-1}$ , $\cos ^{-1}$ and $\tan ^{-1}$ aren’t quite the same as $\dfrac{1}{\textcolor{blue}{\sin}}$ , $\dfrac{1}{\textcolor{limegreen}{\cos}}$ and $\dfrac{1}{\textcolor{red}{\tan}}$ ? Here’s why…

Introducing $\mathbf{\cosec}$ , $\mathbf{\sec}$ and $\mathbf{\cot}$

We have three definitions, now:

Cosecant: $\textcolor{blue}{\cosec x} = \dfrac{1}{\textcolor{blue}{\sin x}}$
Secant: $\textcolor{limegreen}{\sec x} = \dfrac{1}{\textcolor{limegreen}{\cos x}}$
Cotangent: $\textcolor{orange}{\cot x} = \dfrac{1}{\textcolor{red}{\tan x}}$

We’ve given these three reciprocal functions a special name so we don’t get them confused with the inverse functions.

The easiest way to remember which is which, is to look at the third letter of each function, so, Cosecant $= \dfrac{1}{\textcolor{blue}{\sin}}$ , Secant $= \dfrac{1}{\textcolor{limegreen}{\cos}}$ and Cotangent $= \dfrac{1}{\textcolor{red}{\tan}}$ .

In Graphical Form

Now, we’ll represent the graph of $\textcolor{blue}{y = \cosec x}$ :

Notice how there are now asymptotes at $x = -180°, 0°, 180°$ .

Well, $\textcolor{blue}{\cosec x} = \dfrac{1}{\sin x}$ , so it will not have values where $\sin x = 0°$ , i.e. where $x = -180°, 0°, 180°$ .

Notice, also, how there are no values between $y = 1$ and $y = -1$ . Think on that for a while…

Anyway, here’s the graph for $\textcolor{limegreen}{y = \sec x}$ :

See how the asymptotes are now at $x = -270°, -90°, 90°, 270°$ . Again, this is because we’ll find that $\cos x = 0$ at these points.

Again, there are no values between $y = 1$ and $y = -1$

To complete the set, here’s $\textcolor{orange}{y = \cot x}$ :

This time, there are no undefined values for $y$ , but we do have vertical asymptotes at $x = -180°, 0°, 180°$ again.

Domains, Ranges and Key Values

You might want to reference from this table of ranges and domains:

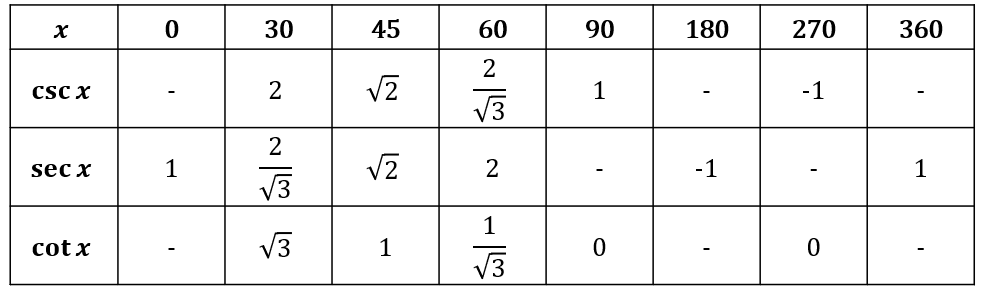
and here’s some key points that you might need to know.

In case you were wondering, $(-1,1)$ means the value is between but not including $-1$ and $1$ .

Reciprocal Trig Functions Example Questions

Question 1: Solve $\sec x = 2$ for all values of $x$ in the range $0° \leq x \leq 720°$ .

[2 marks]

$\sec x = 2$ means that $\cos x = \dfrac{1}{2}$ , which has solutions at $x = 60°, 300°, 420°, 660°$ .

Save your answers with

Gold Standard Education

Sign Up Now

Question 2: Briefly explain why $\cosec x$ and $\sec x$ have no values in the range $(-1,1)$ .

[2 marks]

$\cosec x = \dfrac{1}{\sin x}$ and $\sec x = \dfrac{1}{\cos x}$ .

Since $\sin x$ and $\cos x$ have a minimum of $-1$ and maximum of $1$ , we conclude that $\cosec x$ and $\sec x$ have a positive minimum of $\dfrac{1}{1} = 1$ , and a negative maximum of $\dfrac{1}{-1} = -1$ .

To have $\cosec x$ or $\sec x$ between $-1$ and $1$ , we require $\sin x$ or $\cos x$ to be greater than $1$ , or less than $-1$ , which is not possible.