Differentiation from First Principles

Finding Derivatives from First Principles

To differentiate from first principles, use the formula

$f'(textcolor{blue}{x}) = limlimits_{textcolor{purple}{h} to 0} left( dfrac{f(textcolor{blue}{x} + textcolor{purple}{h}) – f(textcolor{blue}{x})}{textcolor{purple}{h}} right)$

While this might look a little intimidating, it’s pretty easy to understand.

Think about how we describe the gradient between two points for a moment…

$f'(textcolor{blue}{x}) = dfrac{dtextcolor{limegreen}{y}}{dtextcolor{blue}{x}} = dfrac{text{change in }textcolor{limegreen}{y}}{text{change in }textcolor{blue}{x}}$

Well, we can describe a “change in $textcolor{limegreen}{y}$” as $f(textcolor{blue}{x} + textcolor{purple}{h}) – f(textcolor{blue}{x})$ and a “change in $textcolor{blue}{x}$” as the corresponding $textcolor{blue}{x} + textcolor{purple}{h} – textcolor{blue}{x} = textcolor{purple}{h}$

Surely then, as $textcolor{purple}{h}$ decreases toward $0$, we find that the value of the gradient tends toward the actual value, $f'(textcolor{blue}{x})$.

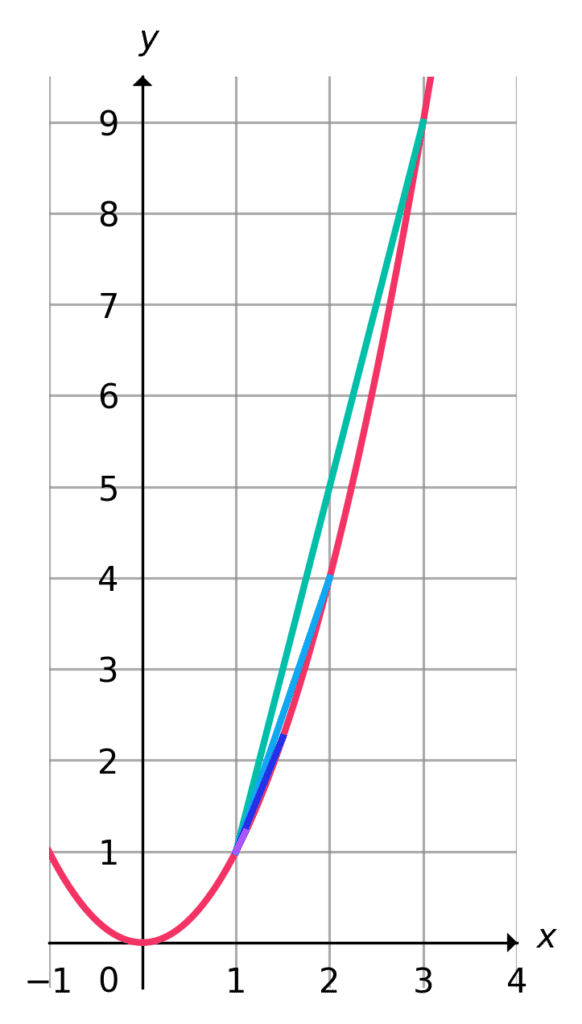
For example, the graph on the right shows the graph $textcolor{limegreen}{y}=textcolor{blue}{x}^2$. It also introduces four “chords”, each indicating the gradient between two points on the graph. As the colour transitions from green to purple, the value of $textcolor{purple}{h}$ is decreasing towards $0$, for the point $(textcolor{blue}{1},textcolor{limegreen}{1})$.

$h=2$ gives $f'(x)=4$

$h=1$ gives $f'(x)=3$

$h=0.5$ gives $f'(x)=2.5$

$h=0.1$ gives $f'(x)=2.1$