Convex and Concave Curves

A LevelAQAEdexcelOCR

Convex and Concave Curves Revision

Convex and Concave Curves

We define a curve $f(x)$ as convex or concave when we observe the behaviour of $f''(x)$ .

Make sure you are happy with the following topics before continuing.

Stationary Points

Distinguishing Between Convex and Concave

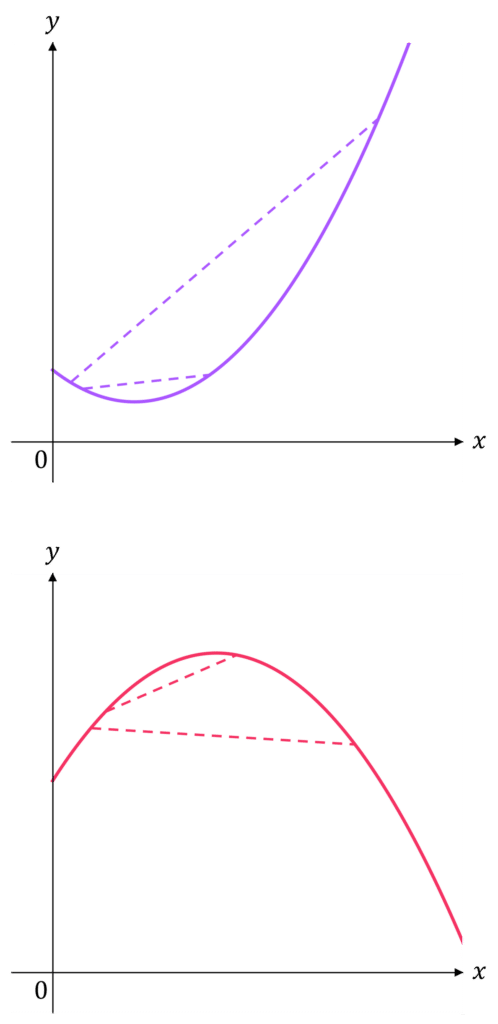
Convex curves curve downwards and concave curves curve upwards.

That doesn’t sound particularly mathematical, though…

When $f''(x) \textcolor{purple}{> 0}$ , we have a portion of the graph where the gradient is increasing, so the graph is convex at this section.
When $f''(x) \textcolor{red}{< 0}$ , we have a portion of the graph where the gradient is decreasing, so the graph is concave at this section.

An easy way to test for both is to connect two points on the curve with a straight line.

If the line is above the curve, the graph is convex.
If the line is below the curve, the graph is concave.

Points of Inflexion

A point of inflexion occurs when the curve transitions from convex to concave or vice versa.

We’re looking for sections of the graph where $f''(x) = 0$ .

Note: While all points of inflexion have $f''(x) = 0$ , not all points where $f''(x) = 0$ are points of inflexion. We have to check the curve actually changes from convex to concave or vice versa by seeing what happens on either side of the point.

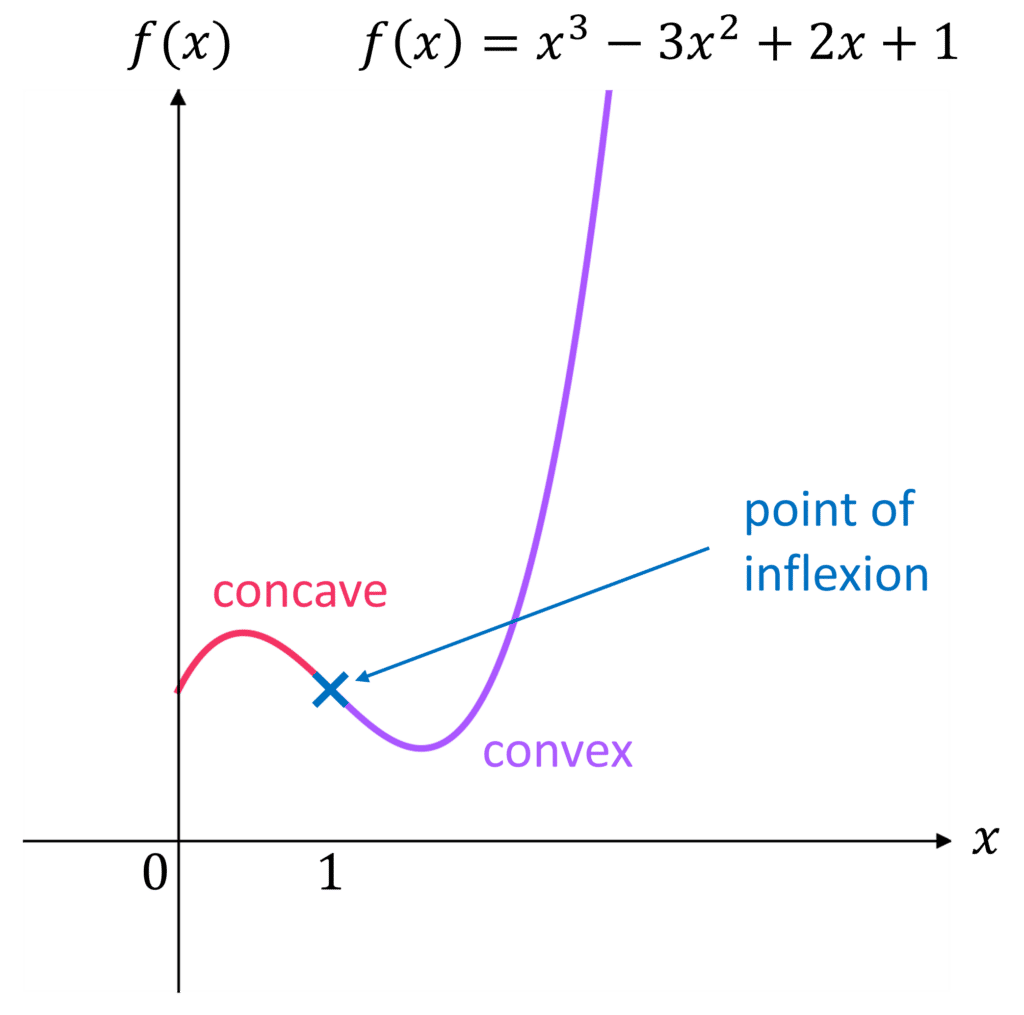
For example, for $f(x) = x^3 - 3x^2 + 2x + 1$

$\begin{aligned} f'(x) &= 3x^2 - 6x + 2 \\ f''(x) &= 6x - 6 \end{aligned}$

So,

$f''(x) = 0$ when $x = 1$

Then,

$f''(x) \textcolor{red}{< 0}$ for $x < 1$

$f''(x) \textcolor{purple}{> 0}$ for $x > 1$

The curve changes from concave to convex at $x=1$ , so there is a point of inflexion at $x = 1$ .

Note: If there is a point of inflexion that is also a stationary point (i.e. $f'(x) = 0$ also), then it is called a stationary point of inflexion.

Example 1: Characterising Graphs

Say we have a graph of the function $f(x) = x(x^2 + 1)$ .

Find the parts of the graph where the function is convex or concave, and find the point(s) of inflexion.

[3 marks]

$f(x) = x(x^2 + 1) = x^3 + x$ gives

$f''(x) = 6x$

$f''(x) = 0$ , when $x = 0$

$f''(x) \textcolor{red}{< 0}$ when $x<0$ . Here we have a concave section.

$f''(x) \textcolor{purple}{> 0}$ when $x>0$ . Here we have a convex section.

When $6x = 0$ , i.e. $x=0$ , we have a point of inflexion, since the curve changes from concave to convex at this point.

So, the function is concave for $x < 0$ , has a point of inflexion at the origin, and is convex for $x > 0$ .

Example 2: Stationary Points of Inflexion

Show that the curve $y = x^3 - 6x^2 + 12x$ has a stationary point of inflexion at $x = 2$

[3 marks]

Find $\dfrac{dy}{dx}$ and $\dfrac{d^2 y}{dx^2}$ :

$\begin{aligned} \dfrac{dy}{dx} &= 3x^2 - 12x + 12 \\[1.2em] \dfrac{d^2 y}{dx^2} &= 6x - 12 \end{aligned}$

When $x = 2$ , $\dfrac{dy}{dx} = 3(2)^2 - 12(2) + 12 = 0$ , so there is a stationary point at $x = 2$

When $x = 2$ , $\dfrac{d^2 y}{dx^2} = 6(2) - 12 = 0$

When $x<2$ , $\dfrac{d^2 y}{dx^2} \textcolor{red}{< 0}$ and when $x>2$ , $\dfrac{d^2 y}{dx^2} \textcolor{blue}{> 0}$ , so there is a point of inflexion at $x=2$ .

Hence, the curve has a stationary point of inflexion at $x=2$ .

Convex and Concave Curves Example Questions

Question 1: Show that $x^4 + 2x^2$ has no points of inflexion.

[3 marks]

Let $f(x) = x^4 + 2x^2$ . Then

$f'(x) = 4x^3 + 4x$ and $f''(x) = 12x^2 + 4$

For any points of inflexion, $f''(x) = 0$ .

Equating $12x^2 + 4 =0$ , we have $x^2 = - \dfrac{1}{3}$ . We are unable to find a (real) root for this, so conclude that there are no points of inflexion.