Revise
Applications of Differentiation
Applications of Differentiation Revision
Applications of Differentiation
In this section, we’ll look at how to use differentiation in mechanics and practical problems.
Make sure you are happy with the following topics before continuing.
A Level Maths Predicted Papers 2025
The MME A level maths predicted papers are an excellent way to practise, using authentic exam style questions that are unique to our papers. Our examiners have studied A level maths past papers to develop predicted A level maths exam questions in an authentic exam format. The profit from every pack is reinvested into making free content on MME, which benefits millions of learners across the country.
A-A* A Level Maths Practice Papers
The MME A-A* A level maths practice papers are excellent for those top achieving students to practise for their exams, using authentic exam style questions that are unique to our practice papers. Our content experts have studied A level maths past papers and specifications to develop specific A-A* A level maths exam questions in an authentic exam style. The profit from every pack is reinvested into making free content on MME, which benefits millions of learners across the country.
Finding Maximum and Minimum Values of Volume and Area
We can use differentiation to find optimal values of dimensions of objects.
So, let’s say wish to create a hollow box of length 2\textcolor{blue}{x}, width \textcolor{blue}{x} and height \textcolor{purple}{h}, and we have a limit of 600\text{ cm}^2 of wood to use.
To find the maximum volume possible, we must find two equations in volume and area:
\textcolor{red}{V} = 2\textcolor{blue}{x} \times \textcolor{blue}{x} \times \textcolor{purple}{h} = 2\textcolor{blue}{x}^2\textcolor{purple}{h}
and
\textcolor{limegreen}{A} = 2(2\textcolor{blue}{x} \times \textcolor{blue}{x}) + 2(2\textcolor{blue}{x} \times \textcolor{purple}{h}) + 2(\textcolor{blue}{x} \times \textcolor{purple}{h}) = 4\textcolor{blue}{x}^2 + 6\textcolor{blue}{x}\textcolor{purple}{h} = 600
Of course, we only want to differentiate in terms of one variable, so we’ll transform the second equation to \textcolor{purple}{h} = \dfrac{300 - 2\textcolor{blue}{x}^2}{3\textcolor{blue}{x}}
Plugging this back into our equation for \textcolor{red}{V}, we have
\textcolor{red}{V} = \dfrac{2\textcolor{blue}{x}^2(300 - 2\textcolor{blue}{x}^2)}{3\textcolor{blue}{x}} = 200\textcolor{blue}{x} - \dfrac{4\textcolor{blue}{x}^3}{3}
We can then differentiate with respect to \textcolor{blue}{x} to find the maximum volume of the box:
\dfrac{d\textcolor{red}{V}}{d\textcolor{blue}{x}} = 200 - 4\textcolor{blue}{x}^2 = 0, giving \textcolor{blue}{x} = \sqrt{50}
We must also verify that this is a maximum, rather than a minimum, so we find \dfrac{d^2\textcolor{red}{V}}{d\textcolor{blue}{x}^2}:
\dfrac{d^2\textcolor{red}{V}}{d\textcolor{blue}{x}^2} = - 8\textcolor{blue}{x} = -8\sqrt{50} < 0, so this is definitely a maximum point.
Therefore, we have \textcolor{blue}{x} = \sqrt{50} and \textcolor{purple}{h} = \dfrac{200}{3\sqrt{50}}, giving \textcolor{red}{V}_{max} = \dfrac{20000}{3\sqrt{50}}.
Finding Rates of Change in Mechanics
In Mechanics, we’ll talk about the derivation of acceleration and velocity from displacement.
From the displacement \textcolor{limegreen}{s}, we can differentiate with respect to \textcolor{purple}{t} to find \textcolor{red}{v}, and differentiate again to find \textcolor{blue}{a}.
So,
\dfrac{d\textcolor{limegreen}{s}}{d\textcolor{purple}{t}} = \textcolor{red}{v}
and
\dfrac{d^2\textcolor{limegreen}{s}}{d\textcolor{purple}{t}^2} = \dfrac{d\textcolor{red}{v}}{d\textcolor{purple}{t}} = \textcolor{blue}{a}
So, for example, let’s say we have an equation for the displacement \textcolor{limegreen}{s} = 2\textcolor{purple}{t}^3 - 3\textcolor{purple}{t}^2 -4\textcolor{purple}{t} + 1.
We can find an equation for the velocity:
\textcolor{red}{v} = 6\textcolor{purple}{t}^2 - 6\textcolor{purple}{t} - 4
and an equation for the acceleration:
\textcolor{blue}{a} = 12\textcolor{purple}{t} - 6
Therefore, we can find the values of \textcolor{purple}{t} such that \textcolor{red}{v} = 0:
6\textcolor{purple}{t}^2 - 6\textcolor{purple}{t} - 4 = 0 has solutions at \textcolor{purple}{t} = \dfrac{1}{2} \pm \sqrt{\dfrac{11}{12}}, but we cannot have a negative time, so we have \textcolor{purple}{t} = \dfrac{1}{2} + \sqrt{\dfrac{11}{12}}.
\textcolor{blue}{a} = 12\left( \dfrac{1}{2} + \sqrt{\dfrac{11}{12}}\right) - 6 = 11.49, so we can conclude that this is a point of minimum displacement.
Applications of Differentiation Example Questions
Question 1: Find the maximum volume possible when we create a hollow box of length 5x, width 3x and height h, and we have a limit of 30000\text{ cm}^2 of wood to use.
[5 marks]
To find the maximum volume possible, we must find two equations in volume and area:
V = 5x \times 3x \times h = 15x^2h
and
A = 2(5x \times 3x) + 2(5x \times h) + 2(3x \times h) = 30x^2 + 16xh = 30000
Of course, we only want to differentiate in terms of one variable, so we’ll transform the second equation to
h = \dfrac{30000 - 30x^2}{16x}
Plugging this back into our equation for V, we have
V = \dfrac{15x^2(30000 - 30x^2)}{16x} = 28125x - 28.125x^3
We can then differentiate with respect to x to find the maximum volume of the box:
\dfrac{dV}{dx} = 28125 - 84.375x^2 = 0, giving x = \sqrt{\dfrac{1000}{3}}
We must also verify that this is a maximum, rather than a minimum, so we find \dfrac{d^2V}{dx^2}:
\dfrac{d^2V}{dx^2} = - 168.75x = -168.75\sqrt{\dfrac{1000}{3}} < 0, so this is a maximum point.
Therefore, we have x = \sqrt{\dfrac{1000}{3}} and h = \dfrac{20000}{16\sqrt{\dfrac{1000}{3}}}, giving V_{max} = \dfrac{6250000\sqrt{3}}{\sqrt{1000}}.
Question 2: A firework is fired directly upwards and has a height of h = 1000\left( \dfrac{t^2}{40} - \dfrac{t^3}{600}\right). Find the time t when the firework finds its maximum height, and state this height.
[4 marks]
h = 1000\left( \dfrac{t^2}{40} - \dfrac{t^3}{600}\right) gives
\dfrac{dh}{dt} = 1000 \left( \dfrac{t}{20} - \dfrac{t^2}{200}\right)
and
\dfrac{d^2h}{dt^2} = 1000 \left( \dfrac{1}{20} - \dfrac{t}{100}\right)
Setting \dfrac{dh}{dt} = 0 gives 1000\left( \dfrac{t}{20}\left( 1 - \dfrac{t}{10}\right) \right) = 0, meaning that t = 0 or t = 10.
Using t=10 gives h=833\text{ m}.
Question 3: Let a bath be modelled as a trapezium with the dimensions shown in the diagram, and width 1\text{ m}. Assuming that water occupies a volume of \dfrac{1}{2}t^2 + 4t\text{ cm}^3, find the amount of time it takes for the bath to fill completely, and find the rate that the water is filling the bath at this point.
[5 marks]
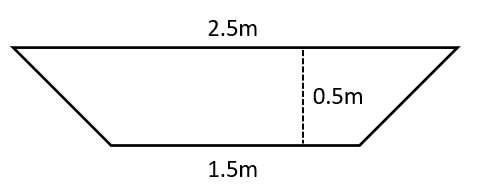
Volume of bath, V:
V = \dfrac{1}{2}(2.5 + 1.5) \times 0.5 \times 1 = 1\text{ m}^3 = 1 \times 10^6 \text{ cm}^3
Then, we must find t such that \dfrac{1}{2}t^2 + 4t - 1000000 = 0.
Using the quadratic formula, we have
t = \dfrac{-4 \pm \sqrt{16 - \left( 4 \times \dfrac{1}{2} \times -1000000 \right)}}{1} = -1418.22, 1410.22\text{ s}
So, we know that the bath takes approximately 23.5\text{ minutes} to fill.
When t = 1410.22, \dfrac{dV_{filled}}{dt} = t + 4, so the water is filling the bath at a rate of 1414.22\text{ cm}^3\text{ s}^{-1}.
