Braking
Braking Revision
Braking
Stopping distance of a vehicle is affected by many different factors. Whether that be the applied braking force, or the driver of the vehicle and their reaction time.
Stopping Distance
Say a car is driving along, and suddenly sees an obstacle ahead. The driver applies the breaks, and the car comes to a stop. This is an emergency stop. The stopping distance is the total distance the car travels between the driver seeing the hazard and the car coming to a stop. So the stopping distance is:
\textcolor{aa57ff}{\text{Stopping Distance} = \text{Thinking Distance} + \text{Braking distance}}
- Thinking distance is the distance travelled during between the driver seeing the hazard, and applying the brakes. It is the drivers reaction time.
- Braking distance is the distance travelled from the point the brakes are applied, to the vehicle coming to a stop. It is the distance travelled while the vehicle is under the braking force.
- The greater the speed of the vehicle, the greater the stopping distance (for a given braking force).
The higher the stopping distance, the more space you should leave between your vehicle and the vehicle in front of you.
Speed and Stopping Distances
If a vehicle is travelling at a higher speed, generally the stopping distance increases. However, thinking distance and braking distance increase at different rates.
As the vehicle speeds up, the thinking distance increases at the same rate as the speed. This is because your reaction time doesn’t really change, but the speed you are going does. So the higher the speed, the more distance will be travelled during your reaction time.
As the vehicle speeds up, the braking distance increases. This is because as there is more speed, there is more kinetic energy due to KE = \dfrac{1}{2} m v^2. Therefore, as the speed increases, the kinetic energy increases at higher rate. This means more work needs to be done to transfer the kinetic energy, so more distance is required as long as the braking force is constant \left( W = Fs\right).
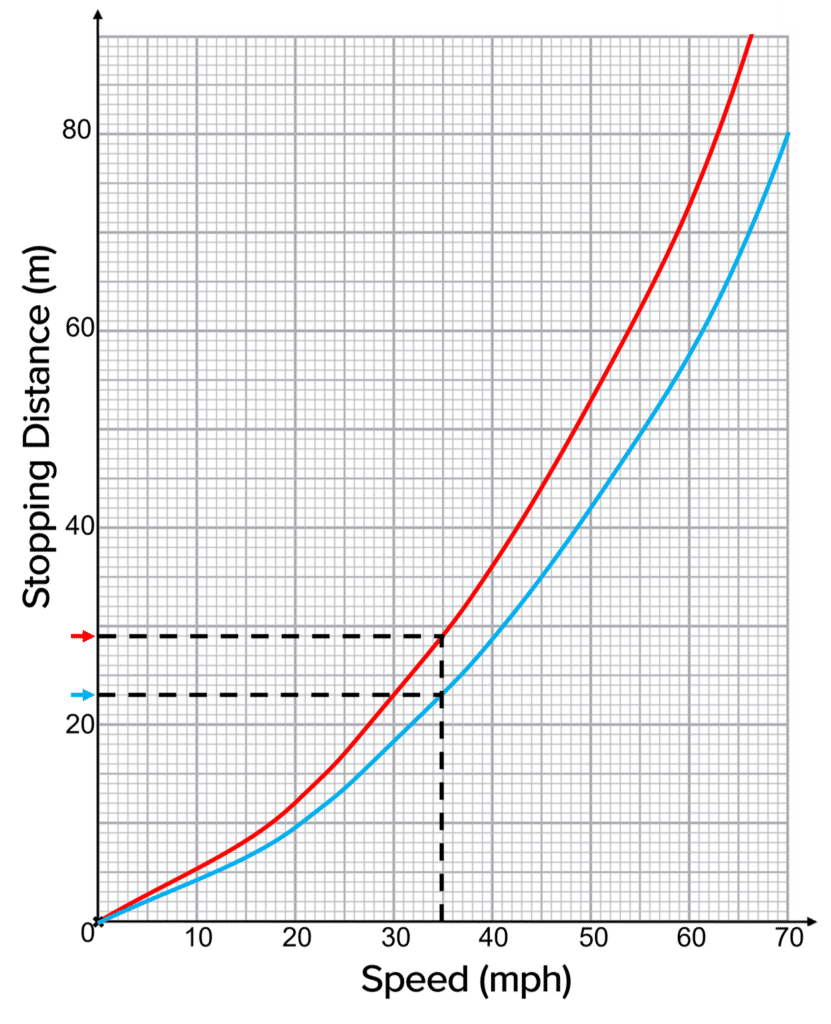
Stopping distance against speed graphs
We can use these graphs to compare different vehicles and their different stopping distances. If you wanted to find out which vehicle had a shorter stopping distance at a certain speed, this can be read off the graph and then compared:
For 35 \: \text{mph}:
Blue Vehicle has a stopping distance of 23 \: \text{m}
Red Vehicle has a stopping distance of 29 \: \text{m}
So the Blue Vehicle had a shorter stopping distance at 35 \: \text{mph}.
Reaction time
Thinking distance is affected by the following factors:
- Speed of the vehicle: the faster the vehicle is travelling, the more distance will be travelled while you react.
- Reaction time: the slower the drivers reaction time, the more distance is travelled before the brakes are applied.
Reaction time is different for everyone. However, most people are within the range of 0.2 and 0.9 seconds.
Factors that can affect reaction time are:
- Tiredness
- Drugs
- Alcohol
- Distractions (i.e on the phone, listening to the radio)
Measuring Reaction Time
We can measure the reaction time of a person. Because our reaction times are less than second, it is not possible to be able to measure the reaction time using an ordinary stop watch. However a simple method we can use is to drop a ruler:
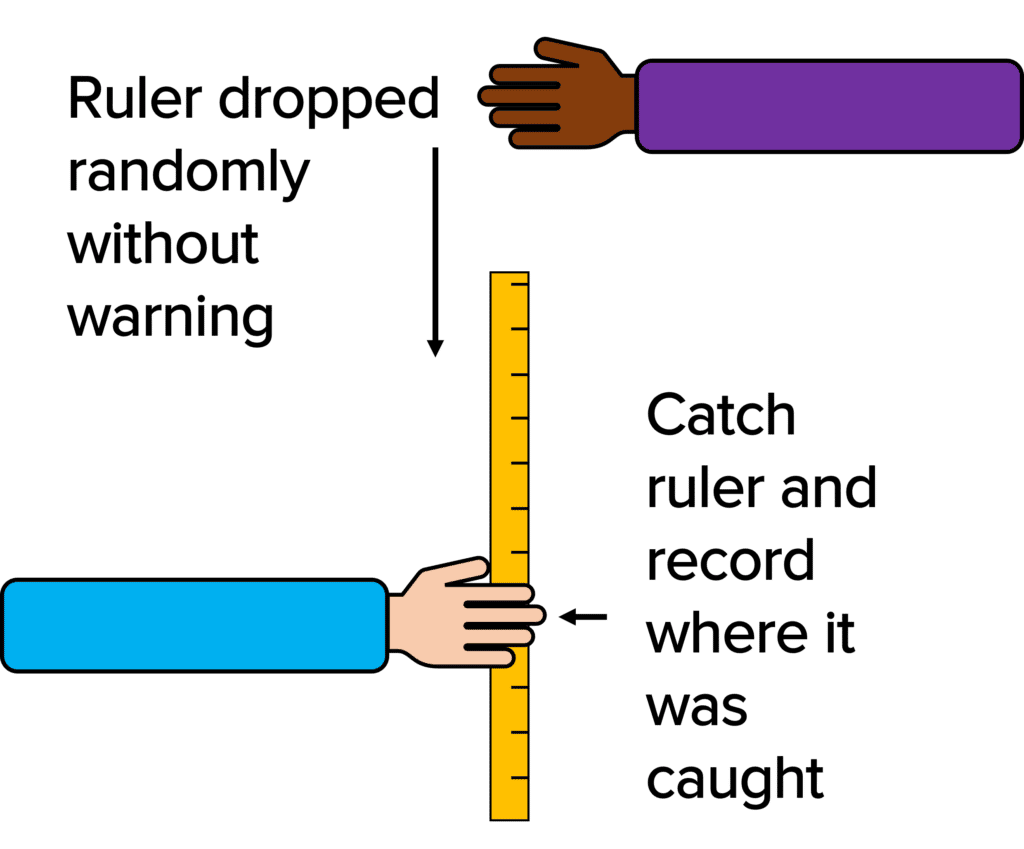
- Position your hand at the 0 \: \text{cm} mark on a ruler. Hover your thumb and forefinger over this point. Have someone hold the ruler from the top.
- Without warning and randomly, the person holding the ruler should drop it and you must try and catch it as quick as you can.
- Where your thumb and forefinger end up is how mush distance the ruler travelled during your reaction time. A longer distance means a longer reaction time.
- As we know the acceleration due to gravity is 9.81 \: \text{m/s}^2, we could use this and the equation \boldsymbol{v^2 = u^2 + 2as} to calculate the actual reaction time.
This accuracy of the experiment could be improved by doing multiple repeats and calculating an average reaction distance or time. You could also test how distractions effect the reaction time.
Factors Affecting Braking Distance
Braking distance is determined by how effective the braking force is. This braking distance can be affected by the following factors:
- Speed of the vehicle: the faster the vehicle is travelling, the more distance you will travel while you react.
- Road/Weather conditions: Wet, snowy or icy conditions reduce the friction between the tyres and the road surface. This means that the car travels further as it will skid on the surface, and the breaking distance will increase.
- Tyre Condition: If the vehicle tyres have reduced tread, this also reduces the friction between the wheel and the tyre surface. This also means that the car travels further as it will skid on the surface.
- Brake Condition: If the vehicles brakes are worn down, friction between the brakes and the wheels is reduced. Hence the braking force will be reduced. This means breaking distance will increase.
Some typical breaking distances for cars at different speeds are:
| Speed of car | Braking Distance |
| \boldsymbol{20 \:} \textbf{mph} | \boldsymbol{6} \: \textbf{m} |
| \boldsymbol{30} \: \textbf{mph} | \boldsymbol{14} \: \textbf{m} |
| \boldsymbol{50} \: \textbf{mph} | \boldsymbol{38} \: \textbf{m} |
| \boldsymbol{70} \: \textbf{mph} | \boldsymbol{75} \: \textbf{m} |
Braking and Work Done
When the driver pushes the brake pedal, they are applying force to the pedal. This force is used to press the brake pads onto the wheels. There is friction between the wheels and the brake pads (in order to slow the wheels down). Work is done here because the friction is causing the kinetic energy of the wheel to be transferred as thermal energy to the brakes. The brakes then increase in temperature as a result.
The faster a vehicle is going, the more energy it has in its kinetic energy store. This means when braking, more work done is required to convert this kinetic energy to thermal energy, and stop the vehicle.
The greater braking force of the vehicle, the greater the deceleration. However, large decelerations could be dangerous. This is because they can lead to the vehicle losing control, or the brakes could overheat.
Example: Estimating Braking Force
A truck is travelling at \textcolor{f95d27}{25 \: \text{m/s}}. The truck brakes to try an avoid an obstacle that is \textcolor{f21cc2}{50 \: \text{m}} in front of it. Calculate the braking force required to stop the truck before the hazard.
The truck has a mass of \textcolor{10a6f3}{30000 \: \text{kg} }.
[3 marks]
We can use \bold{v^2 = u^2 + 2as} as long as we assume that the acceleration is uniform.
The initial velocity \left(u\right) is \textcolor{f95d27}{25 \: \text{m/s}}.
The final velocity\left(v\right) is 0 \: \text{m/s} because the truck needs to stop.
The distance\left(s\right) is \textcolor{f21cc2}{50 \: \text{m}}.
a = \dfrac{v^2 - u^2}{2s}
a = \dfrac{0^2 - \textcolor{f95d27}{25}^2}{2 \times \textcolor{f21cc2}{50}}
a = - 6.25 \: \text{m/s}
We can find the braking force by using the force equation:
F = ma = \textcolor{10a6f3}{30000} \times -6.25
F = -187 500 \: \text{N}
Braking Example Questions
Question 1: A man is driving a car when he sees a hazard ahead. The braking distance of the car is 25 \: \text{m} and the total stopping distance is 34 \text{\:m}. Give the thinking distance of the man.
[1 mark]
\text{Stopping Distance} = \text{Thinking Distance} + \text{Braking distance}
\text{Thinking Distance} = \text{Stopping Distance} - \text{Braking distance}
\textbf{Thinking Distance} \bold{= 34} \bold{- 25}
\bold{=9} \textbf{ m}
Question 2: Use the graph to compare the stopping distances of the two vehicles when they are travelling at 60 \: \text{mph}.
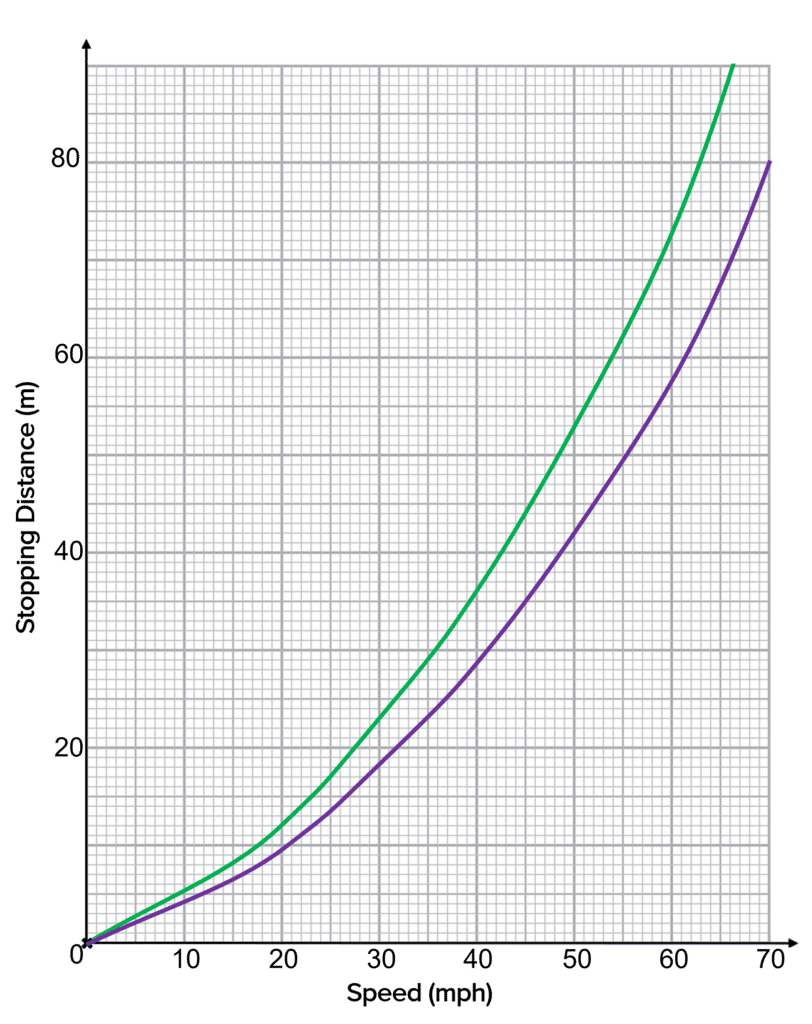 3 marks]
3 marks]
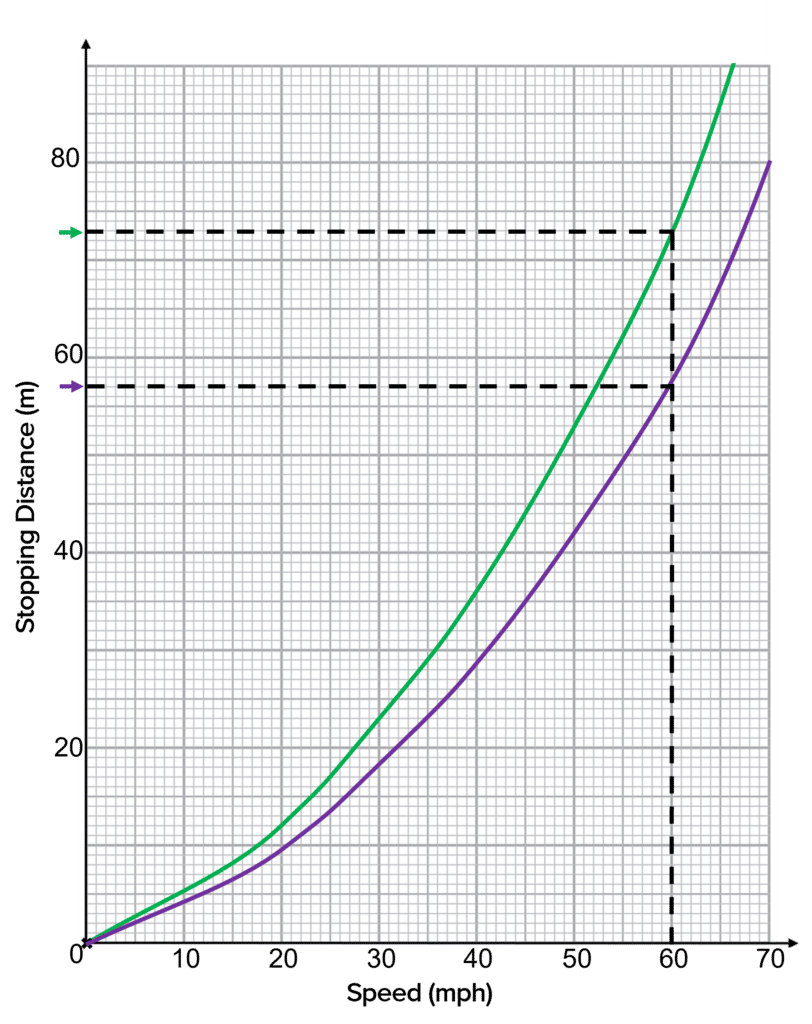
Green Vehicle stopping distance = 73 \:\text{m}
Purple Vehicle stopping distance = 57 \: \text{m}
73 \:\text{m} \: - \: 57 \: \text{m}= 16 \: \text{m}So the green vehicle’s stopping distance is \bold{16 \:} \textbf{m} more than the purple vehicles.
Question 3: Give two factors that might affect a drivers reaction time.
[2 marks]
Any two from:
- Tiredness
- Drugs/Alcohol
- Distractions
Question 4: Give two factors that might affect a vehicles braking distance.
[2 marks]
Any two from:
- Speed of the vehicle
- Road conditions (icy etc.)
- Tyre condition
- Brake condition

MME Premium Membership
£19.99
/monthLearn an entire GCSE course for maths, English and science on the most comprehensive online learning platform. With revision explainer videos & notes, practice questions, topic tests and full mock exams for each topic on every course, it’s easy to Learn and Revise with the MME Learning Portal.
Sign Up Now