Energy Calculations
Energy Calculations Revision
Energy Calculations
The amount of energy stored kinetic, gravitational and elastic potential energy stores can be calculated using different equations. Energy is measured on Joules (J).
Kinetic Energy
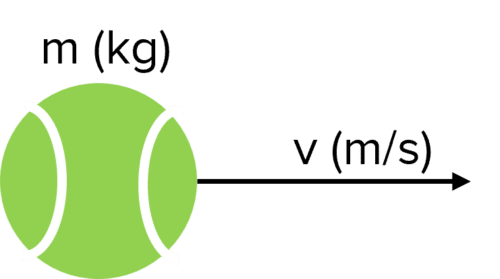
Whenever an object is moving, it has energy in its kinetic energy store. The amount of kinetic energy depends on the mass and velocity of the object.
You can calculate the amount of energy in an object’s kinetic energy store (\bold{E_k}) using the following formula:
E_k = \dfrac{1}{2} m v^2
- m= the mass of the object in kilograms \text{(kg)}
- v= the velocity of the object in metres per second \text{(m/s)}.
Gravitational Potential Energy
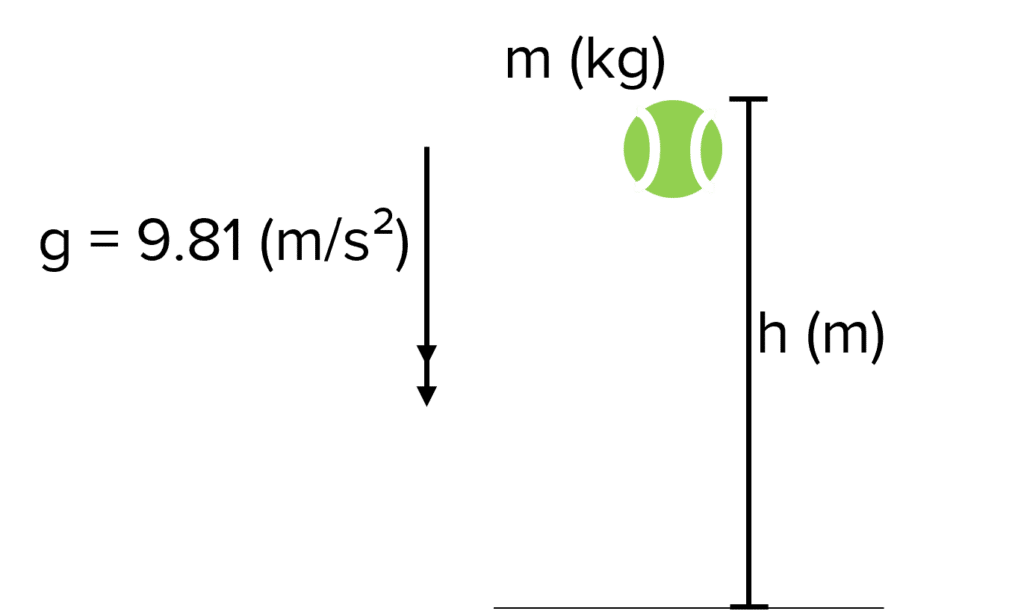
When an object is lifted in a gravitational field, it gains energy in its gravitational potential energy store. The amount of gravitational potential energy depends on the mass of the object, how high it has been lifted and the strength of the gravitational field. On Earth, the gravitational field strength is approximately 9.8\text{ m/s}^2.
The amount of energy in the gravitational potential energy store (\bold{E_p}) can be calculated using the following formula:
E_p = mgh
- m= the mass of the object in kilograms \text{(kg)}
- g= the gravitational field strength in newtons per kilogram \text{(N/kg)}
- h= the change in the height of the object in metres \text{(m)}.
You may have to calculate the height the object has been lifted by subtracting the starting height from the final height.
Elastic Potential Energy
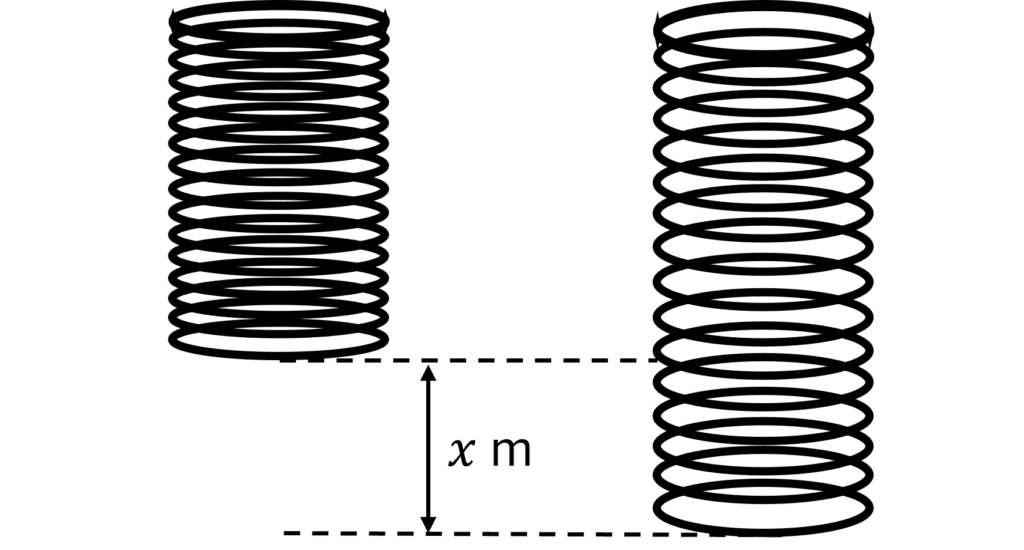
When an object is stretched or squashed, it gains energy in its elastic potential store. The amount of elastic potential energy depends on the extension (distance the object is stretched or squashed) and the spring constant of an object. The spring constant is individual to each object and is measured in Newtons per metre (\text{N/m}).
The amount of elastic potential energy (\bold{E_e}) stored in an object can be calculated using the following formula:
E_e = \dfrac{1}{2} k x^2
- k= the spring constant of the object measured in newtons per metre \text{(N/m)}
- x = the extension (or compression) of the object in metres \text{(m)}. This is shown on the diagram on the right.
You may have to calculate the extension of the object by subtracting the final length from the starting length.
Example: Calculating Elastic Potential Energy
A 10\text{ cm} long wire with a spring constant of 5\text{ N/m} is stretched until it measures 12\text{ cm}. Calculate the potential energy stored by the stretched wire.
Step 1: Calculate the extension of the wire:
\begin{aligned} x &= \color{f21cc2}{12\text{ cm}}- \color{f43364}{10\text{ cm}}\\&= 2\text{ cm}\\&= \color{00bfa8}{0.02\text{ m}} \end{aligned}Step 2: Calculate the elastic potential energy stored by the wire:
\begin{aligned}E_e &= \dfrac{1}{2}kx^2 \\ &=\dfrac{1}{2}\times \color{f95d27}{5\text{ N/m}} \times \color{00bfa8}{(0.02\text{ m})}^2 \\ &= \color{black}{\bold{0.001 \text{ J}}} \end{aligned}
Energy Calculations Example Questions
Question 1: A rubber ball is at rest on the floor. State one way you could increase the energy of the ball and state which store of energy increases.
[2 marks]
Push the ball so that it rolls along the floor. This increases the kinetic energy.
or
Lift the ball above the ground. This increases the gravitational potential energy.
or
Squash the ball. This increases the elastic potential energy.
Accept suitable alternatives.
Question 2: A model airplane has mass 3\text{ kg} and is travelling at 2\text{ m/s}. Calculate the kinetic energy the model airplane is storing.
[2 marks]
E_k= \dfrac{1}{2}\times3\times2^2 = \bold{6\text{ J}}
Question 3: An athlete competing in the high jump jumps 3\text{ m}. Calculate the gravitational potential energy gained by the athlete as they jump to this height. The mass of the athlete is 85\text{ kg}. Give your answer to 2 significant figures.
[2 marks]
Question 4: When stretched, a spring with a spring constant of 10\text{ N/m} increases from 4\text{ cm} long to 5\text{ cm} long. Calculate the energy stored in the spring.
[3 marks]