Revise
Energy Changes
Energy Changes Revision
Energy Changes
When heating up an object, thermal energy is transferred into the object. This causes the object’s temperature to increase. For example, when heating up a pan of soup over a flame, the thermal energy of the flame is transferred to the soup. As the thermal energy in the soup increases, the temperature of the soup increases.
We can calculate how much energy is required to heat up different objects by a specific amount using the concepts discussed on this page.
Specific Heat Capacity
Different materials need different amounts of energy to increase their temperature. The property that determines this is called the specific heat capacity.
The specific heat capacity is represented by a lower-case c and is measured in \text{J/kg} \degree \text{C}.
Materials with a high specific heat capacity need a lot of thermal energy to increase their temperature. Materials with a low specific heat capacity need less thermal energy to increase their temperature.
Some examples of specific heat capacities are shown in the table below.
| Material | Specific Heat Capacity \text{(J/kg}\degree \text{C)} |
| Water | 4200 |
| Aluminium | 900 |
| Ice | 200 |
Heat Change Calculations
To calculate the amount of thermal energy needed to increase the temperature of an object by a given amount, we can use the following equation:
\Delta E=mc\Delta\theta
- \Delta E = the change in thermal energy in joules \text{(J)}
- m = the mass of the object in kilograms \text{(kg)}
- c = the specific heat capacity of the material in joules per kilogram per degree (\text{J/kg} \degree \text{C})
- \Delta \theta = the change in temperature in degrees centigrade or kelvin (\degree \text{C or K)}.
Required Practical
Investigation into Specific Heat Capacity
Doing the experiment
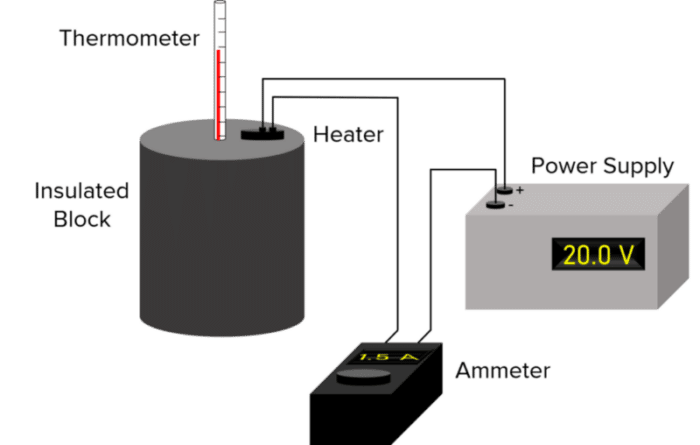
- First, measure the mass of the block using a balance.
- Place the block in a container, surrounded by insulating material (such as bubble wrap) to reduce heat losses from the block.
- Place a thermometer into the container and then connect a power supply, heater and ammeter to the block. This is shown in the diagram below.
- Record the starting temperature of the block using the thermometer.
- Turn the power supply on and start a stopwatch at the same time.
- Record the current \text{(I)} from the ammeter and the potential difference \text{(V)} from the power source.
- After 10 \text{ minutes}, measure the final temperature of the block using the thermometer.
Calculating the specific heat capacity
- Calculate the change in temperature using \Delta\theta=\theta_{final}-\theta_{start}
- Find the power of the heater using the equation P=VI ( rearranged to V= potential difference, I= current).
- The energy transferred from the power source to the heater during the experiment is given by E = Pt (P = the power of the heater, t = the time the heater was switched on =10 \text{ mins or } 600 \text{ s}).
- If we assume that no heat is lost to the surroundings (because the block was insulated), then we know that this is the amount of energy transferred to the block. Hence E = \Delta E.
- By rearranging \Delta E=mc\Delta\theta, we find that c = \dfrac{\Delta E}{m\Delta\theta}.
- Substitute the value of E that you calculated in step 4 and the value of \Delta \theta that you calculated in step 1.
Example: Heat Capacity Calculation
A student carries out an investigation on an unknown material called material X. To calculate its specific heat capacity, the student follows the method described in required practical section of this page. The student records their results in the table below.
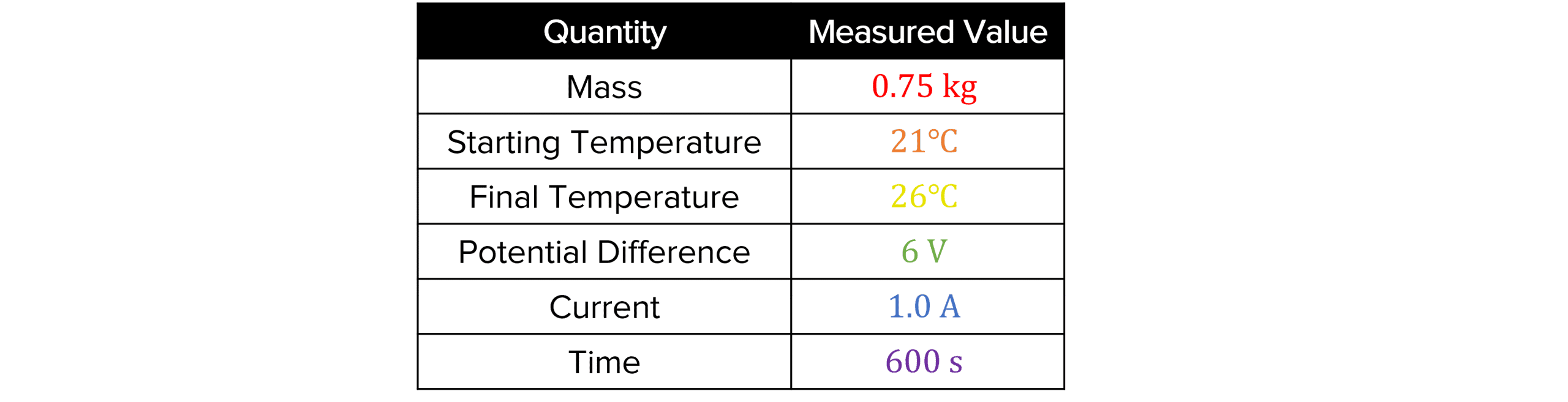
Calculate the specific heat capacity of material X.
[4 marks]
\Delta\theta=\textcolor{d6a504}{26}-\textcolor{f77728}{21}=5\degree C \\P=VI=\textcolor{3da108}{6}\times\textcolor{069ab8}{1.0}=6 \text{ W} \\E=Pt=6\times\textcolor{6c1ac4}{600}=3600\text{ J} = \Delta E \\ c =\dfrac{\Delta E}{m\Delta\theta}=\dfrac{3600}{\textcolor{f50707}{0.75}\times5}=\bold{960}\text{ J/kg}\degree CEnergy Changes Example Questions
Question 1: Material A has a specific heat capacity that is two times bigger than material B. When materials A and B are placed in an oven, which material’s temperature increases faster?
[1 mark]
Material B.
A two times bigger heat capacity means that it takes two times as much energy to raise the temperature of the material by a given amount.
Question 2: A kettle containing 0.5\text{ kg} water heats the water from 22 \degree C to 50 \degree C? How much thermal energy is transferred to the water?
The specific heat capacity of water is 4200 \text{ J/kg} \degree C.
[3 marks]
Question 3: Describe an experiment you could use to determine the specific heat capacity of a block of steel.
[6 marks]
Measure the mass of the block of steel using a balance. Then, wrap the steel block in bubble wrap to reduce heat loss and place it in a container. Place a thermometer into the container and then connect a power supply, heater and ammeter to the container.
Record the starting temperature of the steel block using the thermometer then turn the power supply on and start a stopwatch at the same time. Record the current and potential difference. After 10 \text{ minutes}, measure the final temperature of the block using the thermometer.
Question 4: 500\text{ J} of energy is transferred to a plastic block of mass 5\text{ kg} in order to raise the temperature of the block from 19 \degree C to 24 \degree C. Calculate the specific heat capacity of the plastic.
[3 marks]
MME Premium Membership
£19.99
/monthLearn an entire GCSE course for maths, English and science on the most comprehensive online learning platform. With revision explainer videos & notes, practice questions, topic tests and full mock exams for each topic on every course, it’s easy to Learn and Revise with the MME Learning Portal.
Sign Up Now