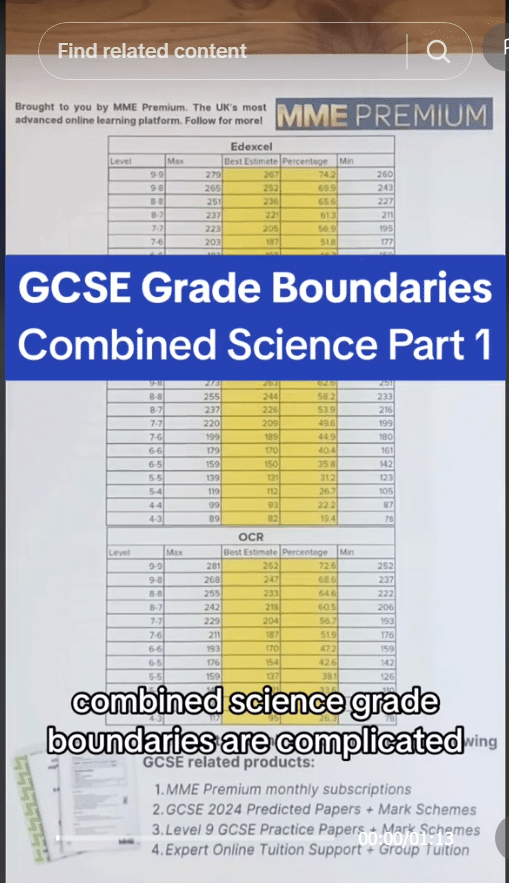
Power
Power Revision
Power
Power is a way to describe how quickly energy is transferred from one store to another or one object to another. For example, the power of your kettle tells you how quickly electrical energy is converted to thermal energy to heat up the water.
Power Definitions and Equations
The definition of power is: the rate at which energy is transferred.
This is the same as saying: the rate at which work is done.
Power is measured in Watts \text{(W)}. One Watt is equal to 1 joule \text{(J)} of energy transfer (or work done) per second \text{s}.
Power can be calculated using either of the following equations:
P=\dfrac{E}{t} P=\dfrac{W}{t}
- P = Power \text{(W)}
- E = Energy transferred \text{(J)}
- W= Work done \text{(J)}
- t = time \text{(s)}
Comparing Power
If you know the power of two otherwise identical machines, you can deduce how quickly they use energy and therefore compare their performance.
For example, microwave oven A has two times the power of microwave oven B. This means that microwave oven A transfers energy into food two times faster than microwave oven B. So, you only have to cook the food for half the time.
Another example is two cyclists. One cyclist is three times more powerful than the other. The more powerful cyclist does work on the bicycle three times faster and therefore travels at three times the speed of the other cyclist.
Example 1: Calculating Power

A car is driving at a constant velocity along a flat road in a 100\text{ m} race.
a) The car uses 50 000\text{ J} whilst driving forwards for 10\text{ s}. Calculate the power of the car’s engine
[2 marks]
P=\dfrac{E}{t}=\dfrac{\textcolor{123196}{50 000}}{\textcolor{00bfa8}{10}}=\bold{5 000\text{ W}}
b) If a different car with a higher power engine uses the same amount of energy, which care will finish the race first? Assume that both cars are identical except for the engine.
[1 mark]
The higher power car will finish the race first. The engine transfers more energy to kinetic energy in the same time and so the car travels faster.
Example 2: Calculating Power Using Work Done
It takes 50 \text{ kJ} of work for a crane to lift a storage container and place it on top of another. The storage container is in the air for 50 \text{ s}, calculate the power of the crane. State the units of your answer.
[3 marks]
\begin{aligned}\bold{P} &=\bold{\dfrac{W}{t}} \\ &= \dfrac{\textcolor{f21cc2}{50 000 \text{ J}}}{\textcolor{aa57ff}{50 \text{ s}}}\\ &= \bold{1000} \textbf{ W} \end{aligned}
Power Example Questions
Question 1: A power source is connected to a motor for 30\text{ s}. In this time, it supplies 150\text{ J} electrical energy to the motor. Calculate the power of the motor.
[2 marks]
Question 2: A student does 10\text{ J} work on a ball as they lift it 1m from the ground. It takes them 0.5\text{ s} to lift the ball. Calculate the power of the student.
[2 marks]
Question 3: Two lightbulbs are connected to batteries in two identical circuits. Bulb A has power 6\text{ W} and bulb B has power 10\text{ W}. What can you deduce about the brightness of the two bulbs? Explain your answer.
[2 marks]
Bulb B is brighter than bulb A.
Because bulb B has a higher power, energy is transferred into light faster in bulb B and so it is brighter.