Momentum
Momentum Revision
Momentum
Momentum is a property of all moving objects. It depends on mass and velocity.
Momentum
Momentum is a vector, meaning it has magnitude and direction. It is defined by the equation:
\textcolor{aa57ff}{p = mv}
- \textcolor{aa57ff}{p} is the momentum in kilogram metres per second \left(\text{kg m/s}\right).
- \textcolor{aa57ff}{m} is the mass in kilograms \left(\text{kg}\right).
- \textcolor{aa57ff}{v} is the velocity in metres per second \left(\text{m/s}\right).
This equation can be used to work out the momentum of a moving object. A stationary object has no momentum \left(\text{because} \: \textcolor{aa57ff}{v} = 0 \: \text{m/s}\right).
Conservation of Momentum
In a closed system, the total momentum before an event is equal to the total momentum after an event. This is the conservation of momentum.
Example:
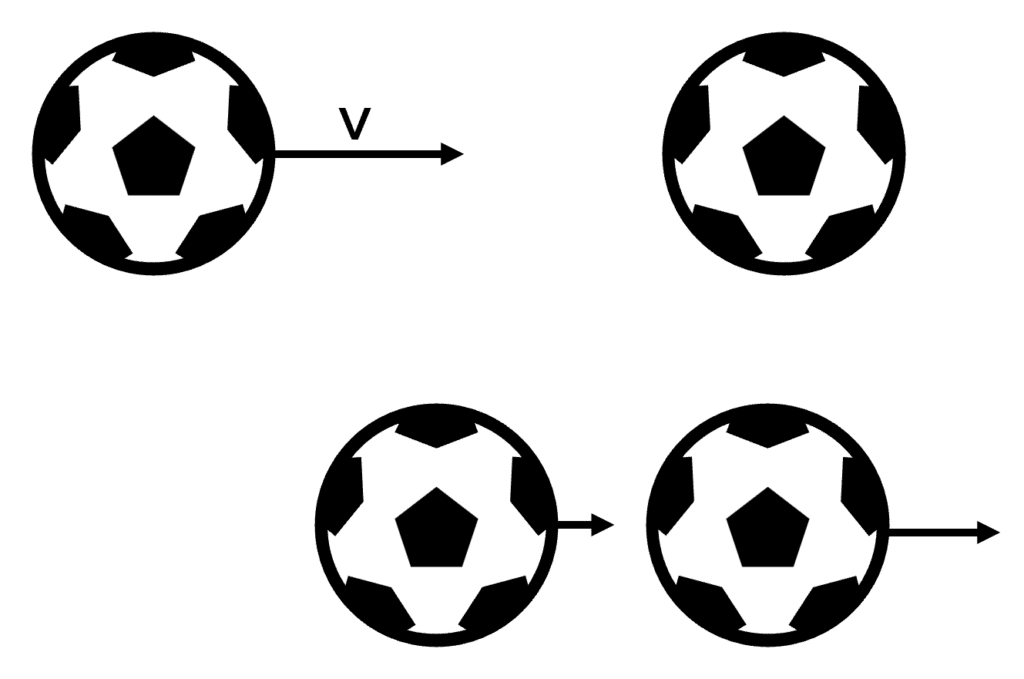
A football is kicked at a stationary football, at a velocity of v. They both have the same mass of m. The momentum before they collide is just the sum of the momentum of each ball:
\text{total momentum before} = \left( m \times v\right) + \left( m \times 0 \right) \text{total momentum before} = mv
So the total momentum before the collision is just the momentum of the moving ball, because the other ball is not moving and so has no momentum.
The total momentum after they collide will be equal to mv. Ball B now has velocity and hence it has momentum. Ball A now moves with less velocity. So the sum of these two momentums will be equal to the total momentum before the collision mv.
Changes in Momentum
We know that when a resultant force acts on an object, it causes it to accelerate. Acceleration is a change in velocity. So if a force causes an object’s velocity to change, then it also changes the objects momentum \left(p = mv\right).
We can combine the equations for Newton’s 2nd Law and acceleration to express force as a change in momentum:
Newton’s 2nd Law: F = ma. Acceleration: a = \dfrac{v-u}{t}.
Combine them to get: F = \dfrac{m\left(v-u\right)}{\Delta t}
This can be written as:
\textcolor{00bfa8}{F = \dfrac{m \Delta v}{\Delta t}}
- \textcolor{00bfa8}{F} is the Force in Newtons \left(N\right)
- \textcolor{00bfa8}{m \Delta v} is the change in momentum in kilograms \left(\text{kg m/s}\right). \textcolor{00bfa8}{m} is the mass and \textcolor{00bfa8}{\Delta v} is the change in velocity.
- \textcolor{00bfa8}{\Delta t} is the change in time.
A faster rate of change of momentum means a bigger force. So if an object changes velocity very quickly, it’s momentum will change very quickly. Therefore there is a larger force on the object.
Because of this, there are often safety measures on vehicles in order to reduce the rate of change of momentum, and hence the reduce force on passengers. This reduces injuries on passengers. Some vehicle safety measures are:
- Seat belts – these stretch so that the time taken for the passenger to stop is longer.
- Air bags – these inflate when there is a crash, in order to slow the passenger down.
Other examples of safety measures include:
- Gymnasium crash mats and cushioned surfaces for playgrounds – They are cushioned so increase the time taken to fall. This decreases the rate of change of momentum and hence decreases the force on the gymnast.
- Cycle helmets – foam inside the helmet is crushable so increases the time taken for your head to stop.
Example: Calculations involving momentum with a collision
Two cars crash head on into each other and both come to rest. The momentum after the crash is \textcolor{00bfa8}{0 \: \text{kg m/s}}. The diagram shows the velocities and masses of the two cars before the collision. Calculate the velocity of car A before the collision, \textcolor{aa57ff}{v_A}. Momentum is conserved.

[3 marks]
If the momentum after the collision is \textcolor{00bfa8}{0 \: \text{kg m/s}}, then the momentum before the collision must also be 0 \: \text{kg m/s}.
Therefore the momentum of the two vehicles must add up to zero. This means the momentum of each vehicle must be equal:
\text{Momentum of Car A} = \text{Momentum of Car B}
Using the momentum equation, p = mv:
m_A \times \textcolor{aa57ff}{v_A} = m_B \times v_B
Substitute in the values:
\textcolor{00d865}{1000 \: \text{kg}} \times \textcolor{aa57ff}{v_A} =\textcolor{f95d27}{1500 \: \text{kg}} \times \textcolor{ed1111}{9 \: \text{m/s}}
Rearrange to find the velocity of Car A:
\textcolor{aa57ff}{v_A} = \dfrac{\textcolor{f95d27}{1500} \times \textcolor{ed1111}{9}}{\textcolor{00d865}{1000}}
\textcolor{aa57ff}{v_A} = 13.5 \: \text{m/s}
Momentum Example Questions
Question 1: A toy car of mass 0.6 \: \text{kg} travels with a velocity of 3 \: \text{m/s}. Calculate the momentum of the toy car.
[2 marks]
p = mv
p = 0.6 \: \text{kg} \times 3 \:\text{m/s}
p = \bold{1.8 \: }\textbf{kg m/s}
Question 2: Explain what is meant by the conservation of momentum.
[2 marks]
In a closed system, the total momentum before an event is equal to the total momentum after an event.
Question 3: A bowling ball travelling at a velocity of 3.5 \: \text{m/s} hits a stationary pin.
After the collision, the bowling ball moves at a velocity of 1 \: \text{m/s}.
Calculate the velocity of the pin after the collision. Momentum is conserved.
The mass of the bowling ball is 6 \: \text{kg} and the mass of the pin is 2 \: \text{kg} .
[4 marks]
\text{total momentum before} = \left( 6 \: \text{kg} \times 3.5 \: \text{m/s} \right) + \left( 2 \: \text{kg} \times 0 \: \text{m/s} \right) = 21 \:\text{kg m/s}
\text{total momentum after} = \left( 6 \: \text{kg} \times 1 \: \text{m/s} \right) + \left( 2 \: \text{kg} \times ? \: \text{m/s}\right)
\text{total momentum before} = \text{total momentum after}
21 \: \text{kg m/s} = 6 + \left(2 \times ? \right)
\text{Velocity of pin} = \dfrac{21-6}{2}= \bold{7.5 \:} \textbf{kg m/s}
Question 4: A car decelerates from a speed of 20 \: \text{m/s} to 10 \: \text{m/s}, in 25 \:\text{seconds}. The car has a mass of 1200 \: \text{kg}. Calculate the force felt by the car.
[3 marks]
F = \dfrac{m \Delta v}{\Delta t}
Change in velocity = 20 - 10 = 10 \: \text{m/s}
F = \dfrac{1200 \times 10}{25} = \bold{480 \:} \textbf{N}






