Newton's Laws of Motion
Newton's Laws of Motion Revision
Newton’s Laws of Motion
Isaac Newton devised the three laws of motion in the 1660s. They describe how an object moves as a result of a force (i.e stationary, at a constant speed or accelerating).
Newton’s First Law
Newton’s 1st law states:
When the resultant force on an object is zero:
- If the object is stationary, it remains stationary.
- If the object is moving, then it continues to move at the same speed and direction (so the same velocity).

Because there is no resultant force acting on an object, the forces are balanced. For example, on a car moving at a constant velocity, the driving force is equal to the resistive forces of drag.
Therefore the speed/velocity of an object can only change when the forces are not balanced, and there is a resultant force. This is acceleration. For example, the forces on the car are balanced until the driving force is increased. There is now a resultant force in the forwards direction and the car accelerates.
Newton’s Second Law
Newton’s 2nd law states that:
- Force and acceleration are directly proportional: \bold{\textcolor{f21cc2}{F \propto a}}
- Acceleration and mass are inversely proportional: \bold{\textcolor{f21cc2}{a \propto \dfrac{1}{m}}}
Combing these two facts gives the equation:
\textcolor{f21cc2}{ F = ma}
- F is the force in Newtons \left( \text{N} \right)
- m is the mass in kilogram \left( \text{kg}\right)
- a is the acceleration in metres per second squared \left( \text{m/s}^2 \right)
We know from Newton’s 1st law, that if there is a resultant force on an object then there is acceleration. Newton’s 2nd law tells us that when this force increases, the acceleration increases proportionally. It also tells us that an object of less mass will accelerate more (for the same force).
Required Practical
Investigating the effect of varying mass and force on acceleration of an object.
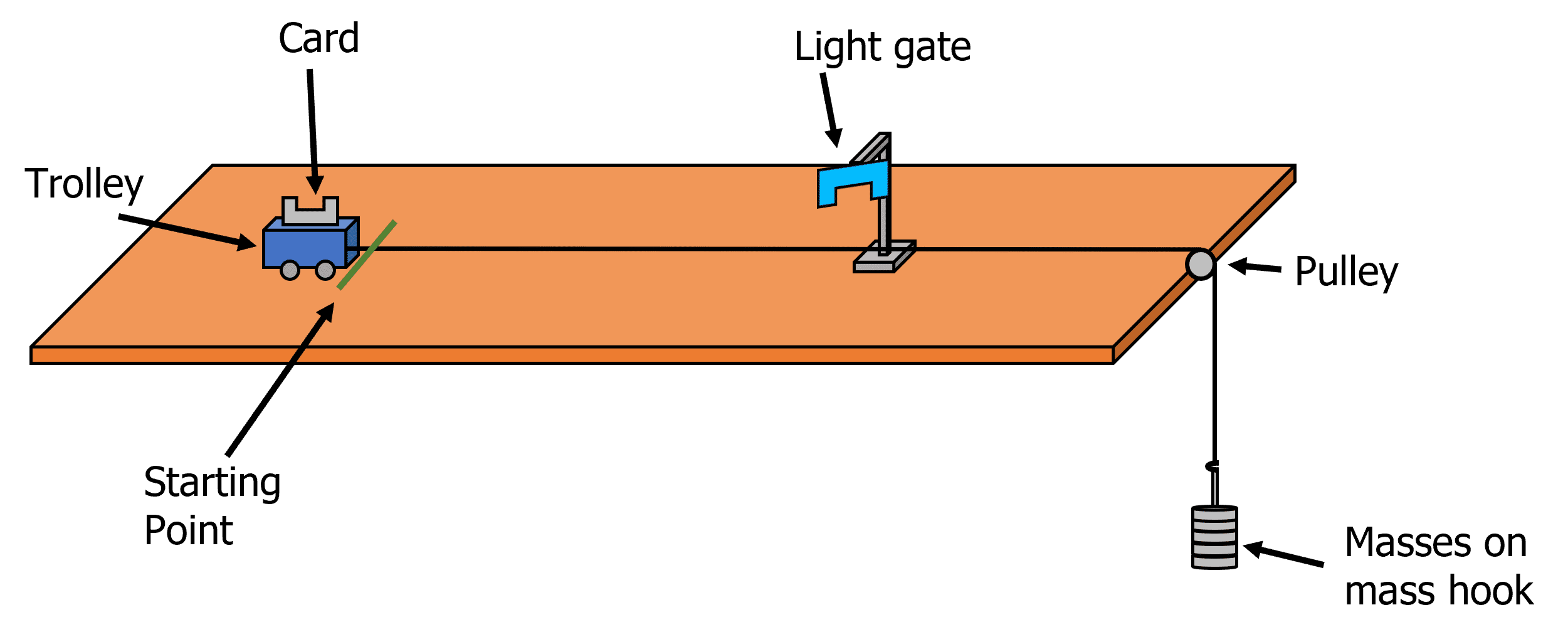
This experiment tests Newton’s 2nd law, \bold{\textcolor{00bfa8}{F = ma}}. It involves using masses and a trolley pulley system
The piece of card on top of the trolley has a segment cut out so that the light gate is triggered twice; once when the front end of the vehicle passes through the gate and again when the back end of the vehicle passes through the gate. This can be used in computer software to measure the velocity of the trolley as it passes through the light gate, and how long it takes. This is then used to calculate the acceleration of the trolley.
Doing the Experiment
- Set up the experiment as shown in the diagram below.
- The trolley is connected to the masses by a string through a pulley. The weight of these masses will be the force used in the calculations. Any reasonable mass is fine \left(\text{e.g.} 1 \: \text{kg}\right).
- Mark a starting point on the surface that you’re doing the experiment. The trolley must start at this point every time. Hold the trolley stationary at the start line, making sure that the string is not loose.
- Release the trolley. Record the acceleration of the trolley that the light gate measures.
- Repeat this at least two more times with the same masses, and calculate an average acceleration. This will be the average acceleration of the whole system.
-
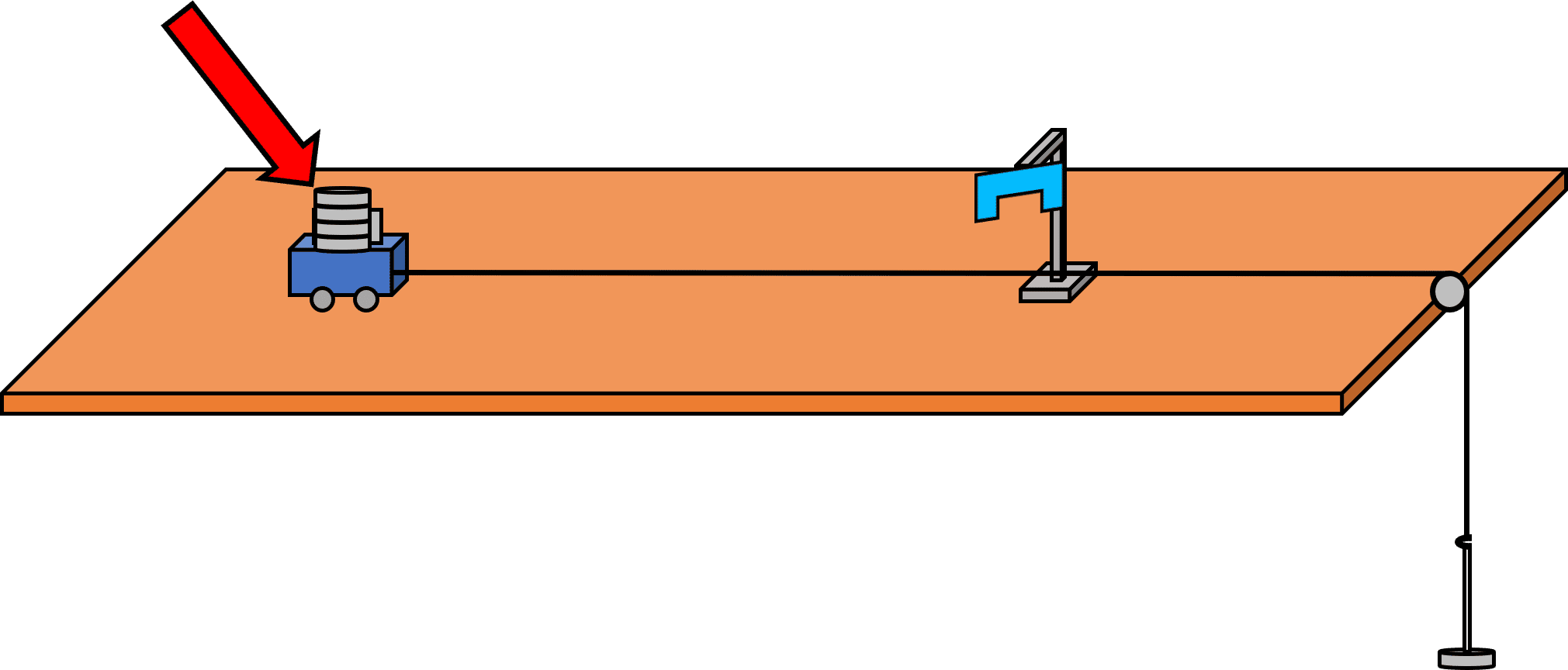
To investigate varying mass:
The mass we’re concerned with in this experiment is the mass of the trolley (not the masses on the mass hook). So, to investigate how varying mass affects the acceleration of the trolley:
- Use same the experimental method, but each time add more mass to the trolley (not on the mass hook), and record the average acceleration.
- The force is kept constant, because the force is the weight of the masses on the hook.
- So as more masses are added to the trolley, the acceleration should decrease because \bold{\textcolor{00bfa8}{a = \dfrac{F}{m}}}.
-
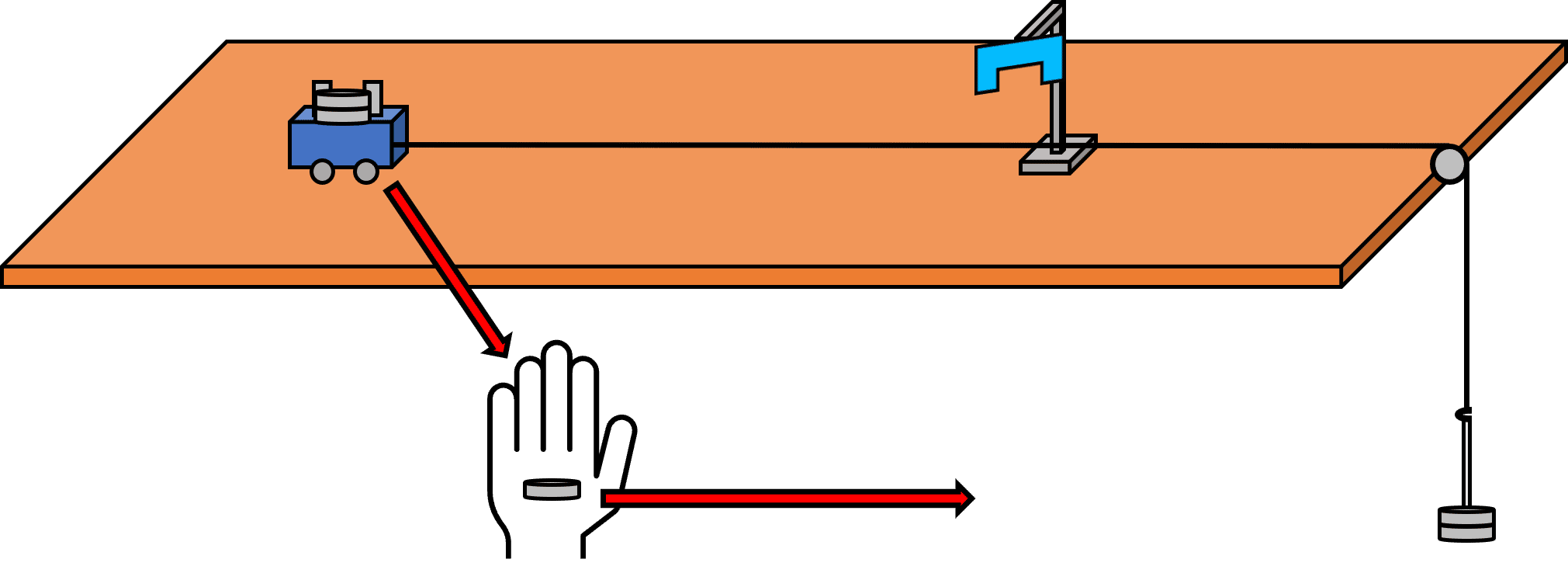
To investigate varying force:
The force we’re concerned with now is the weight of the masses on the hook. However, in order to investigate the effect of force on acceleration, the mass of the whole system needs to stay constant. So to investigate the force, we need to change the force applied without changing the mass:
- Use same the experimental method, however start with all masses on the trolley.
- Then take a mass off the trolley, add it to the hook, and record the acceleration each time. This way, the mass of the whole system is not changing (because the mass is just being transferred from one place in the system to another).
- The acceleration should increase as the force increases because \bold{\textcolor{00bfa8}{F = ma}}.
Newton’s Third Law
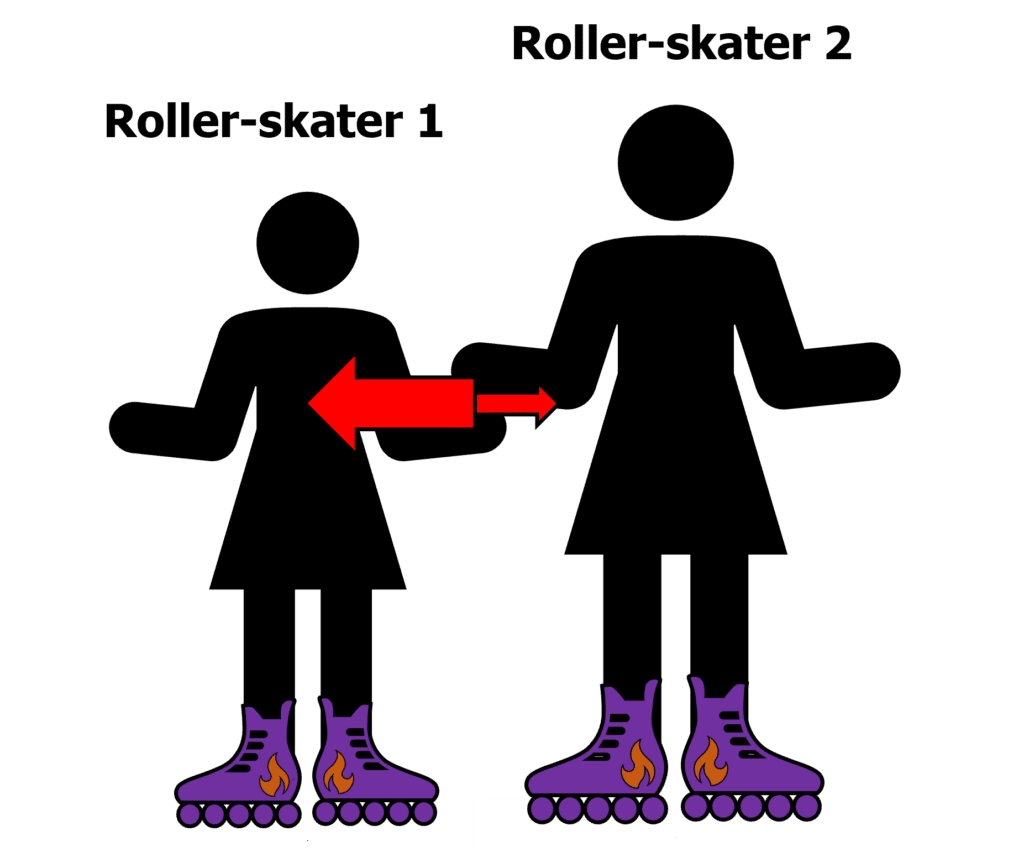
Newton’s 3rd law states: Whenever two objects interact, the forces they exert on each other are equal and opposite.
So if you kick a football, the football exerts an equal and opposite force on you. Or if you push a box, the box pushes back on you equally as hard.
If the forces are equal, then you may think that means that the objects remain stationary. However, each force acts on different objects with often different masses, so this is not the case.
Newton’s 3rd law can be seen when one roller-skater pushes on another:
- Roller-skater 1 pushes on roller-skater 2.
- Roller-skater 2 feels this force from roller-skater 1, and roller-skater 1 feels an equal but opposite force from roller-skater 2.
- Both roller-skaters feel the same force, but just in opposite directions (equal and opposite). And so the roller-skaters move away from each other.
- Because they have different masses, they accelerate differently. Roller-skater 1 is smaller and has less mass, so accelerates more because \bold{ \textcolor{10a6f3}{a \propto \dfrac{1}{m}}} .
Newton’s 3rd law can also be seen in situations in equilibrium, such as a book on a table. The force applied on the table due to the weight of the book is equal and opposite to the normal contact force of the table on the book. The book is pushing on the table and the table is pushing back, with equal force.
Inertia
Say an object is stationary, or is moving at a constant speed. Inertia is the tendency of this object to continue either in this state of rest or at this constant velocity.
Inertial mass measures how difficult it is to change the velocity of an object. It is the force divided by the acceleration (Newton’s 2nd law):
\textcolor{f95d27}{m = \dfrac{F}{a}}
Example: Calculating acceleration and force
A car accelerates at \textcolor{10a6f3}{4 \: \text{m/s}^2} . The resultant force causing the acceleration is \textcolor{f21cc2}{44 \: \text{N}}. Calculate the mass of the car.
[3 marks]
\bold{F = ma} is Newton’s 2nd Law.
Rearrange to find mass: \bold{m = \dfrac{F}{a}}
Substitute in the values: \bold{m = \dfrac{\textcolor{f21cc2}{44}}{\textcolor{10a6f3}{4}}}
\bold{m = 11 \: \textbf{kg}}
Newton's Laws of Motion Example Questions
Question 1: Explain how a vehicle moving at a constant speed will continue moving at a constant speed. You should reference Newton’s 1st law in your answer.
[3 marks]
Newtons 1st law states that an object will continue to move at the same speed if the resultant force acting on it is zero.
Therefore, the vehicle will continue moving at a constant speed as long as no resultant force is acting on it.
There is no resultant force because the driving force and resistive forces (such as air resistance) will be balanced.
Question 2: Box A is pushed along the floor, with a force exerted on it. Box B is also pushed along the floor, with the same force exerted on it. Box B is heavier than box A. Which box accelerates more? Explain your answer.
[3 marks]
We know acceleration is inversely proportional to mass:
\bold{a = \dfrac{F}{m} \:}\text{or}\bold{ \: a \propto \dfrac{1}{m}} .
Therefore, Box A accelerates more because it has less mass.
Question 3: A runner of mass 60 \: \text{kg} exerts 23 \: \text{N} of force to accelerate. Calculate the runners acceleration.
[3 marks]
\bold{F = ma} is Newton’s 2nd Law.
Rearrange to find mass: \bold{a = \dfrac{F}{m}}
Substitute in the values: \bold{a = \dfrac{23}{60}}
\bold{a = 0.38 \: \textbf{m/s}^2} \text{(2 sf)}
Question 4: State what is meant by inertial mass.
[1 mark]
The inertial mass of an object is a measure of how difficult it is to change it’s velocity.






