Revise
Resultant Force
Resultant Force Revision
Resultant Force
Multiple forces can act on an object at one time, and we can use the idea of a resultant force to determine the direction of motion of the object. The resultant force can be calculated and shown in vector diagrams.
What is resultant force?
If multiple forces act at the same point, we can consider them as one single force that has the same effect as all the original forces acting together. This new force is called the resultant force.
So the resultant force is a sum of all the forces acting on an object. It gives the actual direction and magnitude of the overall force on the object.
If two forces are acting in a straight line (parallel), then we can work out the resultant force very easily:
- If the forces are acting in the same direction, we add them to find the resultant force.
- If the forces are acting in the opposite direction, we subtract them to find the resultant force.
If there is no resultant force on an object, the forces are balanced and the object doesn’t move. The object is in equilibrium.
Free Body Diagrams
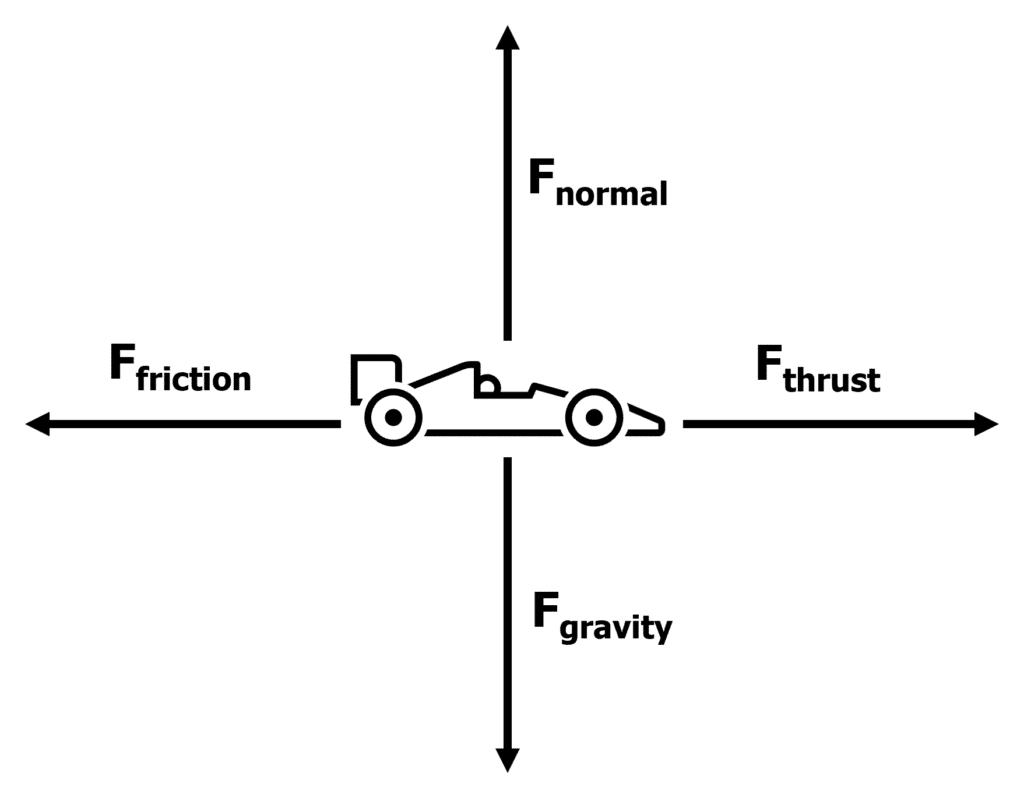
Free body diagrams are used to represent the forces acting on an object. The arrows represent each force and the direction they act.
An example of a free body diagram is shown on the right. It shows the different forces that might act on a toy car.
We can use the toy car as an example:
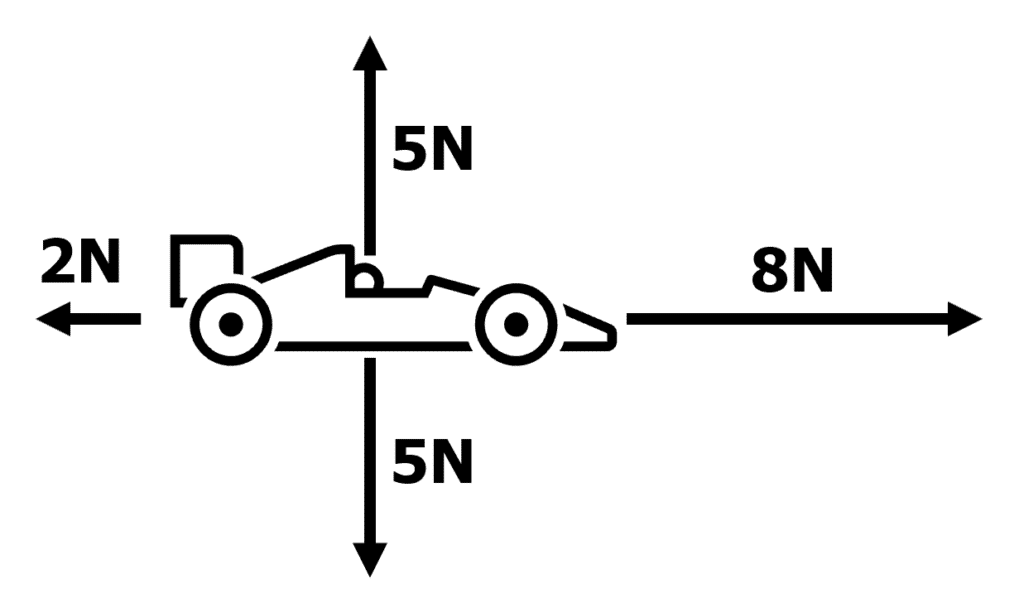
In the diagram on the right, the forces have been given magnitudes. The toy car is initially completely stationary, and then the forces shown act on it. We can work out the vertical and horizontal resultant forces acting on the toy car:
The vertical resultant force is 5 \: \text{N} - 5 \: \text{N} = 0 \: \text{N}. We subtract these forces because they are parallel and act in opposite directions.
The horizontal resultant force is 8 \: \text{N} - 2 \: \text{N} = 6 \: \text{N}. Again we subtract because they are parallel and act in opposite directions.
Therefore the resultant force is 6 \: \text{N} forwards (to the right), and the toy car accelerates. Because the vertical forces add up to 0 \: \text{N}, the car stays vertically stationary.
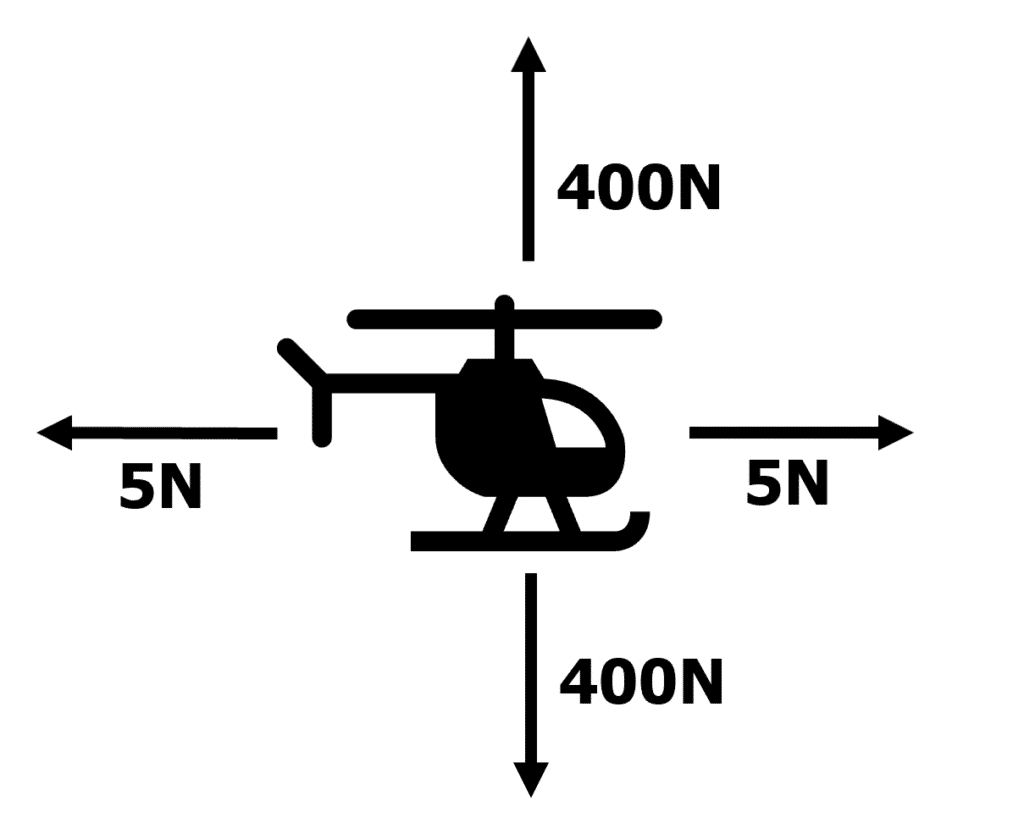
Another example is shown on the right. The resultant forces on the helicopter can be calculated:
- Horizontal resultant force: 5 \: \text{N} - 5 \: \text{N} = 0 \: \text{N}
- Vertical resultant force: 400 \: \text{N} - 400 \: \text{N} = 0 \: \text{N}
Because the resultant forces are both zero \left(0 \: \text{N}\right) on the object, the forces acting on the object are balanced. Therefore object is in equilibrium. This means the helicopter is not accelerating in any direction, and therefore is either stationary or travelling at a constant speed.
Vector Diagrams
Vector diagrams are a more scientific and accurate way of representing forces. The following rules must be followed when drawing a vector diagram:
- The forces are drawn to scale, so the length of the lines must be scaled to the magnitude of the force.
- They must be drawn tip to tail.
- The resultant force is then represented by drawing an arrow from the start of the first force to the end of the second force.
As long as diagrams are to scale, we can work out the resultant force by measuring the line we have drawn.
We can also find the direction of the resultant force by measuring one of the angles shown on the diagram in purple. This can be done using a protractor. This angle can be measured from either the horizontal or the vertical, as long as this is stated i.e “the resultant force is 30\text{°} from the horizontal”.
Example: Using Vector Diagrams
A speed boat on a river has a driving force of 20\: \text{N} north. It is a windy day on the river, and so there is 5 \: \text{N} force west on the boat due to this wind. Find the direction and the magnitude of the speed boat.
[3 marks]
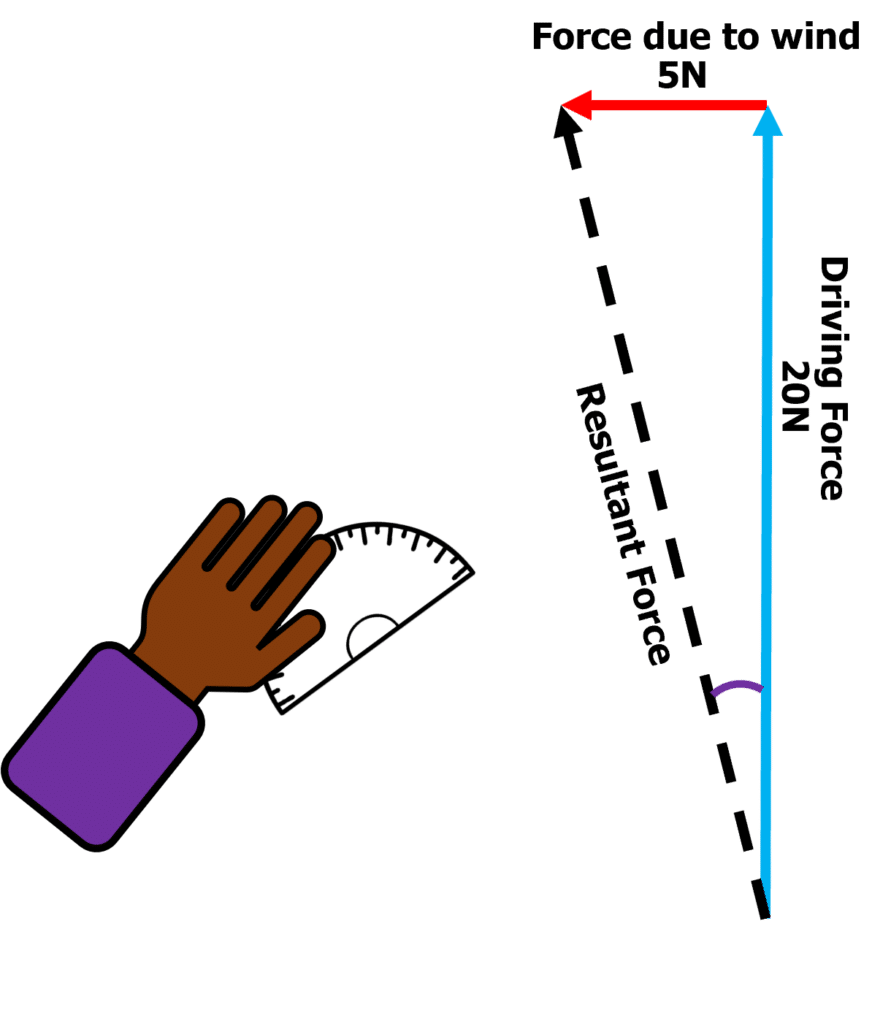
- Firstly, we must draw a vector diagram illustrating the forces.
- Make sure this is drawn to a scale, for example this scale could be 1 \: \text{cm} = 1 \: \text{N} .
- As long as it is drawn to a scale, the angle can simply be measured by a protractor.
- Measuring the angle in purple, we get approximately 14°.
So the angle of the resultant force is 14° from the driving force. This can be written as a bearing of 346° from the north.
If you knew the scale, you could also measure the distance of the resultant force using a ruler. This length can then be used with the scale to work out the magnitude of this resultant force.
Resultant Force Example Questions
Question 1: All the forces on an object are balanced. What is the resultant force on the object?
[1 mark]
Question 2: Calculate the resultant force on the object.
[1 mark]
\bold{2} \: \textbf{N} to the left.
Question 3: The resultant force on an object is 5 \: \text{N} to the right and 12\: \text{N} upwards. Calculate the missing forces on the free body diagram.
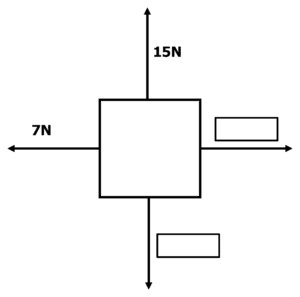
[2 marks]
MME Premium Membership
£19.99
/monthLearn an entire GCSE course for maths, English and science on the most comprehensive online learning platform. With revision explainer videos & notes, practice questions, topic tests and full mock exams for each topic on every course, it’s easy to Learn and Revise with the MME Learning Portal.
Sign Up Now