Rearranging Equations
Rearranging Equations Revision
Rearranging Equations
Like in maths, sometimes in science you will have to rearrange equations. This allows you to work out a value from the equation that isn’t usually the subject.
How to Rearrange Equations
The aim of rearranging equations is to get your new value (the subject) on its own. For example, you may want to rearrange E=mc^2 to make c the subject. This means your answer should start with c=.
To achieve this, you need to perform operations (add, subtract, multiply, divide, square, square root etc) on the equation. Remember, each operation must be performed on BOTH sides of the equation. You may need to perform more than one operation to fully rearrange your equation. Make sure you do the operations in the opposite order to BIDMAS. In other words, move the variables not attached to your subject first.
Example: Rearrange v=ut+\dfrac{1}{2} at^2 to make u the subject.
[2 marks]
First we need to subtract \dfrac{1}{2} at^2 from both sides:
\begin{aligned} v\textcolor{d11149}{-\dfrac{1}{2} at^2} &= ut + \dfrac{1}{2} at^2 \textcolor{d11149}{-\dfrac{1}{2} at^2} \\ v- \dfrac{1}{2} at^2 &= ut \end{aligned}Then we divide by t:
\begin{aligned}\dfrac{v-\dfrac{1}{2} at^2}{\textcolor{d11149}{t}} &= \dfrac{ut}{\textcolor{d11149}{t}} \\ \dfrac{v- \dfrac{1}{2} at^2}{t} &= u \end{aligned}So our answer is:
\bold{u = \dfrac{v- \dfrac{1}{2} at^2}{t}}For more examples, visit the rearranging formulas page from the MME maths revision course.
Pyramid Rearranging
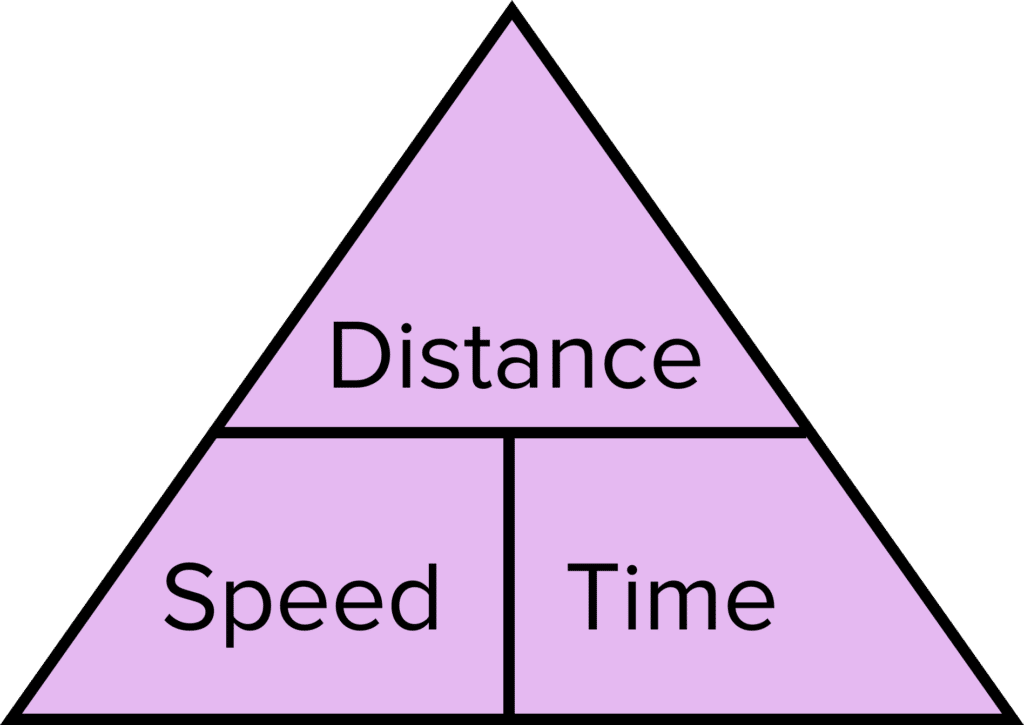

For some equations, we can use a pyramid to help us rearrange.
For example, if you need to rearrange \text{speed}=\dfrac{\text{distance}}{\text{time}} you fill in the bricks on the pyramid as shown on the right.
Write the value from the top of the fraction in the top brick of the pyramid and the value from the bottom of the fraction in one of the bottom bricks. Write the other value in the remaining bottom brick.
From this pyramid, we can make any value the subject.
If your equation has a multiplication instead of a fraction, the two multiplied numbers go in the two bottom bricks.
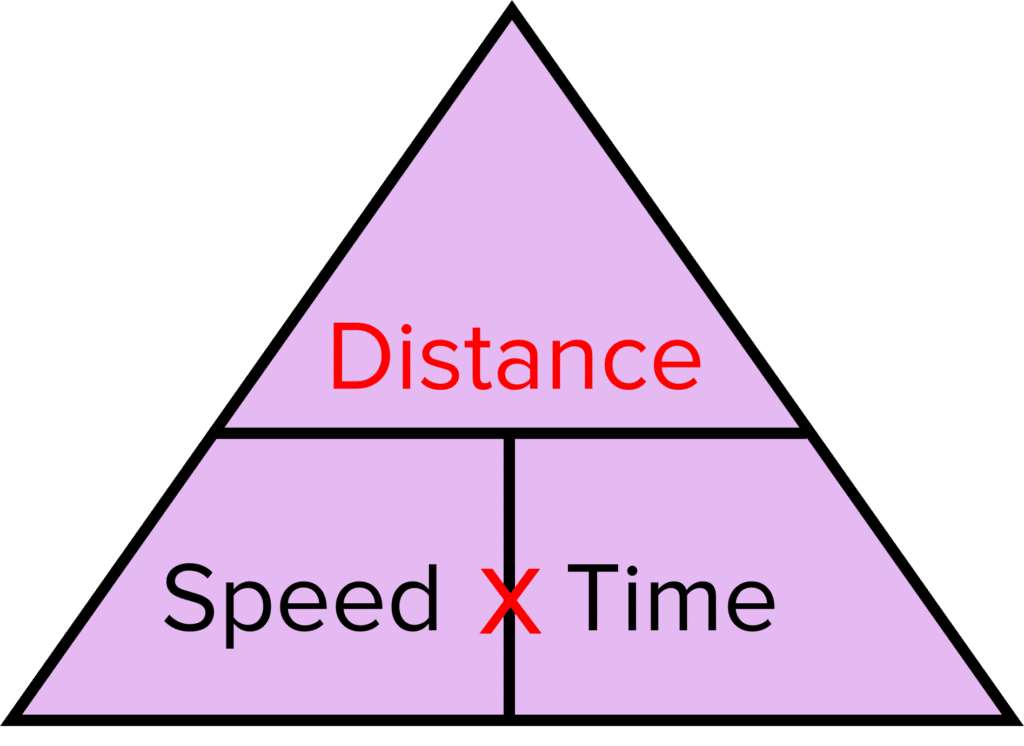

If we want to make distance the subject:
Speed and time are next to one another. This means we multiply them.
\textbf{distance} \bold{=} \textbf{speed} \bold{\times} \textbf{time}
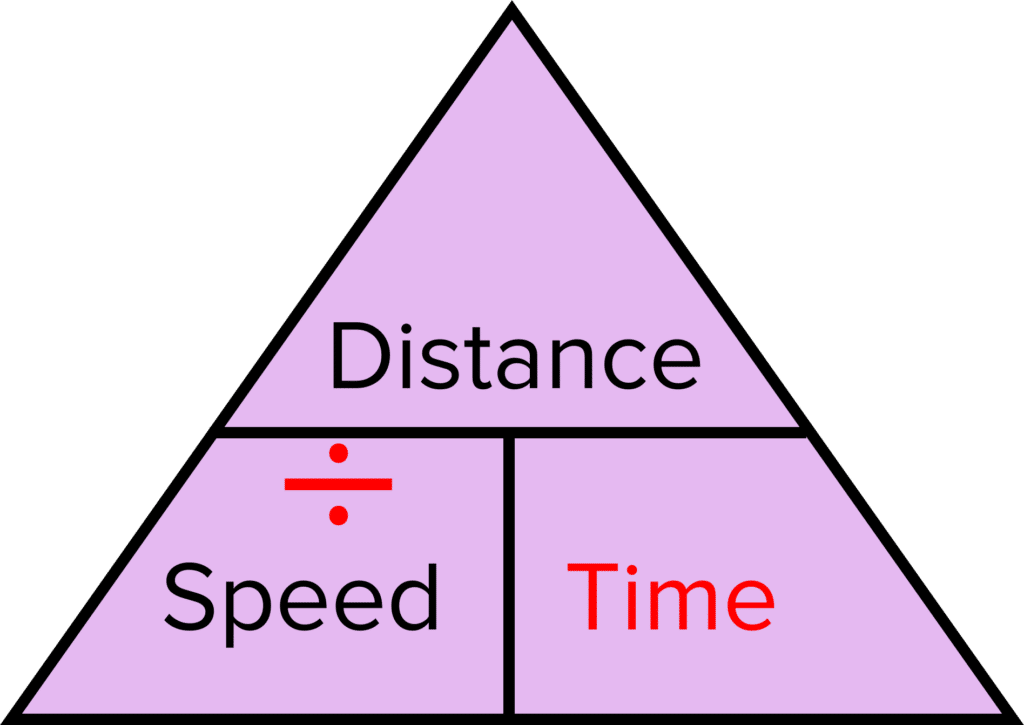

If we want to make time the subject:
Distance is on the brick above speed. This means we divide distance by speed.
\textbf{time} \bold{=} \dfrac{\textbf{distance}}{\textbf{speed}}
But remember this method only works for equations with three values that are multiplied or divided!
Rearranging Equations Example Questions
Question 1: Why can the pyramid rearranging method not be used to rearrange the following equation?
a= b \times c + d
[2 marks]
The pyramid method can only be used for equations with three values.
The pyramid method can only be used for equations where the values are multiplied or divided.
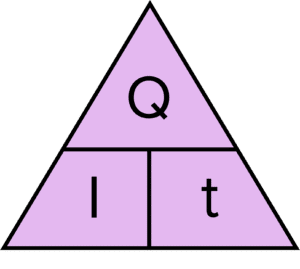
Question 2: Use the pyramid method to rearrange Q=It to make t the subject.
[2 marks]
Question 3: Rearrange the following equation to make c the subject:
Q=mc\Delta T
[3 marks]
Divide both sides by \bold{m}:
\dfrac{Q}{m}=c \Delta T
Divide both sides by \bold{\Delta T}:
\dfrac{Q}{m\Delta T}=c
(Can perform the previous two steps in any order)
So:
\bold{c=\dfrac{Q}{m \Delta T}}