Back to GCSE Science Revision Home

Back to GCSE Science Revision Home

Useful Formulae

GCSEAQAFoundationHigher

Useful Formulae Revision

Useful Formulae

This page contains useful formulae you may need in your exams. You should already be familiar with these equations from GCSE maths.

Area Calculations

Area is the amount of space that a 2D shape takes up.

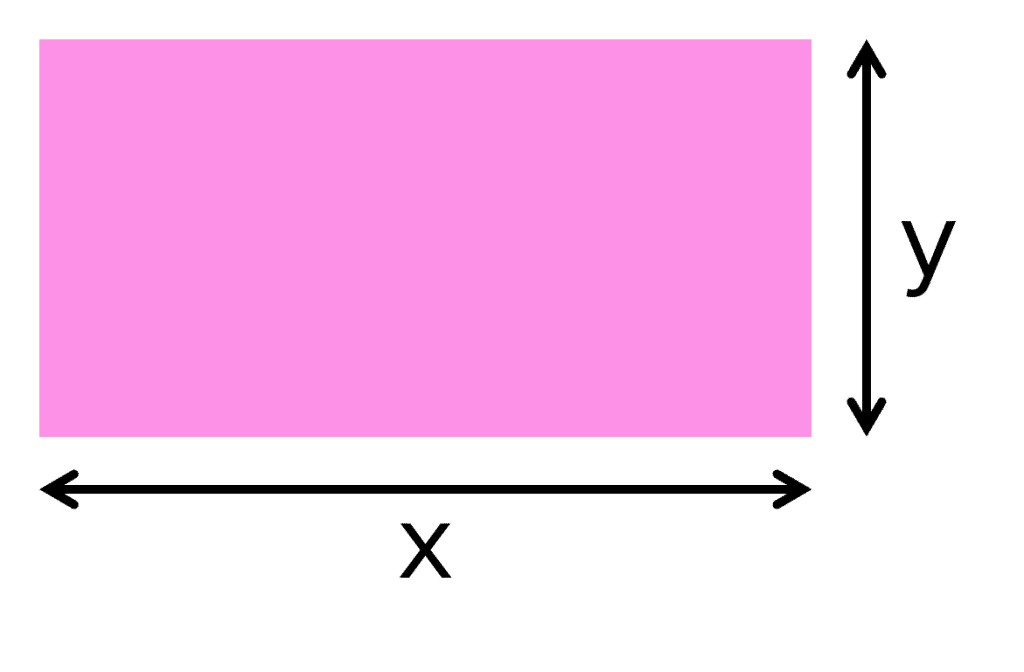
Squares and Rectangles

$A=xy$

$x=$ length
$y=$ height

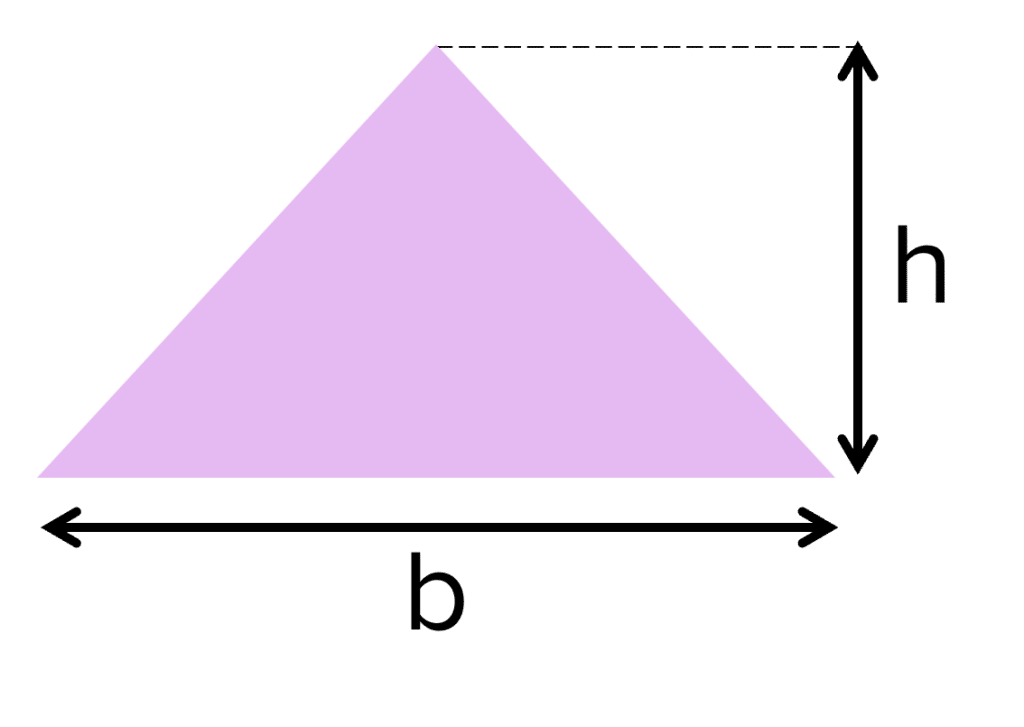
Triangles

$A=\dfrac{1}{2}bh$

$b=$ base
$h=$ height

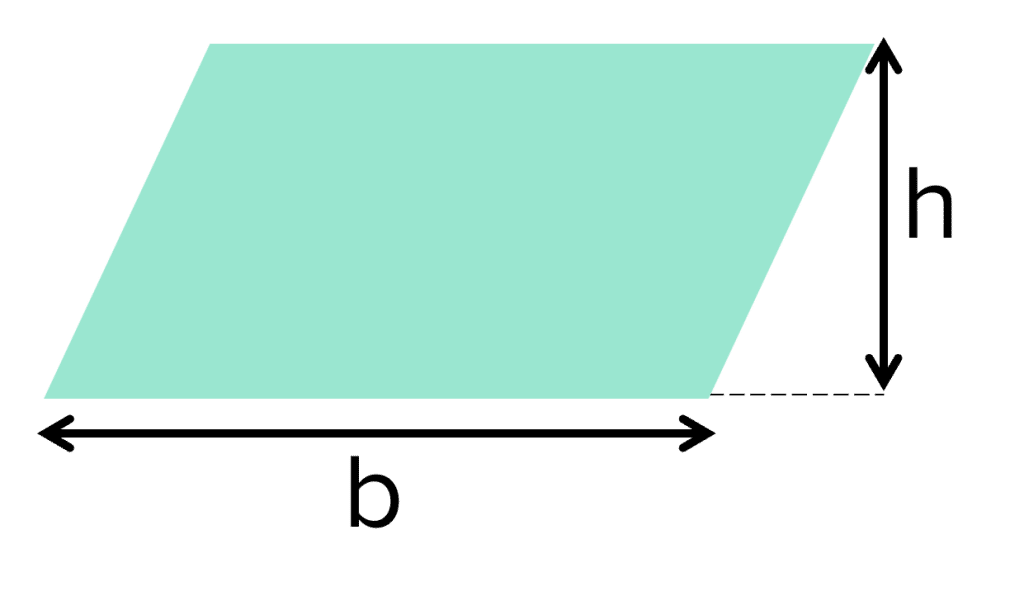
Parallelograms

$A=bh$

$b=$ base
$h=$ perpendicular height

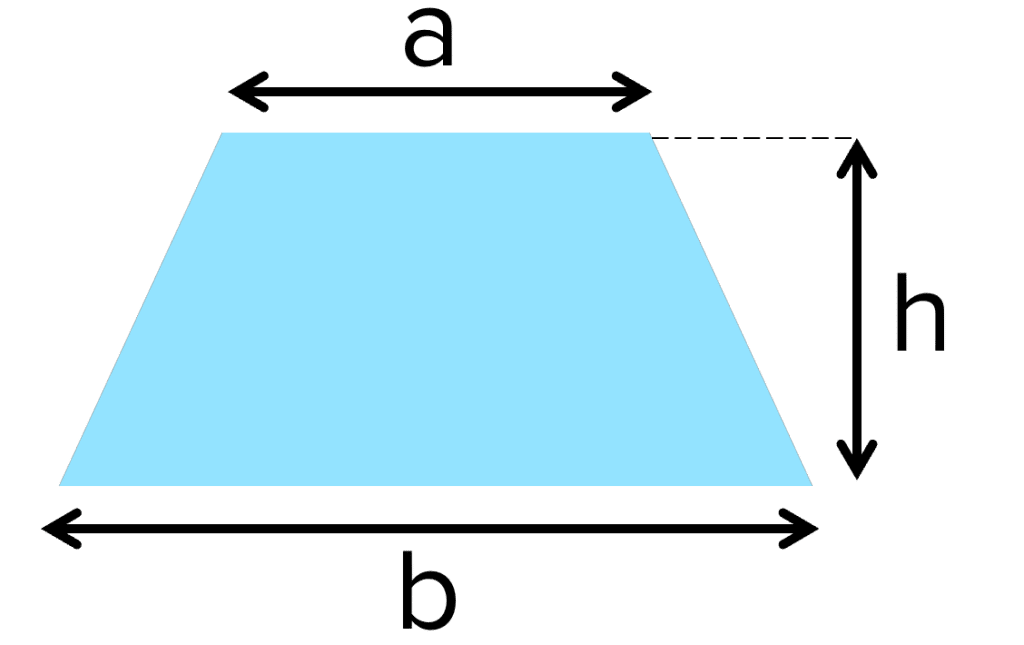
Trapezia

$A=\dfrac{1}{2}(a+b)h$

$a=$ width of the short side
$b=$ width of the long side
$h=$ height

Circles

You should know what the following words mean when talking about circles:

Radius – the distance between the entre of the circle and any point on the edge of the circle.
Diameter – the distance between two opposite edges of the circles, passing through the centre.
Circumference – the distance around the edge of the circle.

Area of a Circle

$A=\pi r^2$

$r=$ radius

Circumference

$C=2 \pi r = \pi d$

$r=$ radius
$d=$ diameter $=2r$

Volume Calculations

Volume is the amount of space a 3D shape takes up.

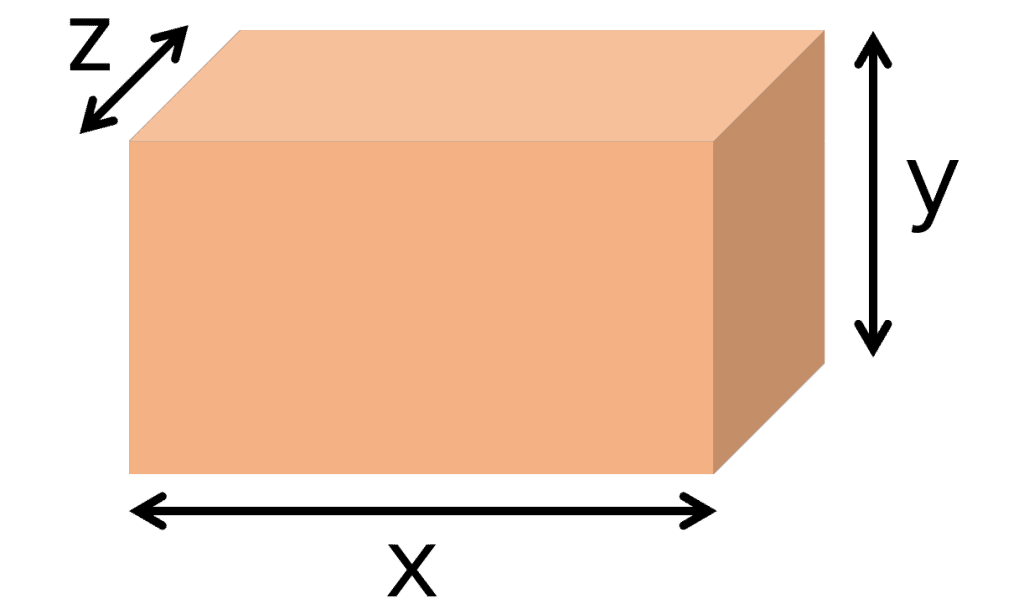
Cuboid

$V=xyz$

$x=$ width
$y=$ height
$z=$ length

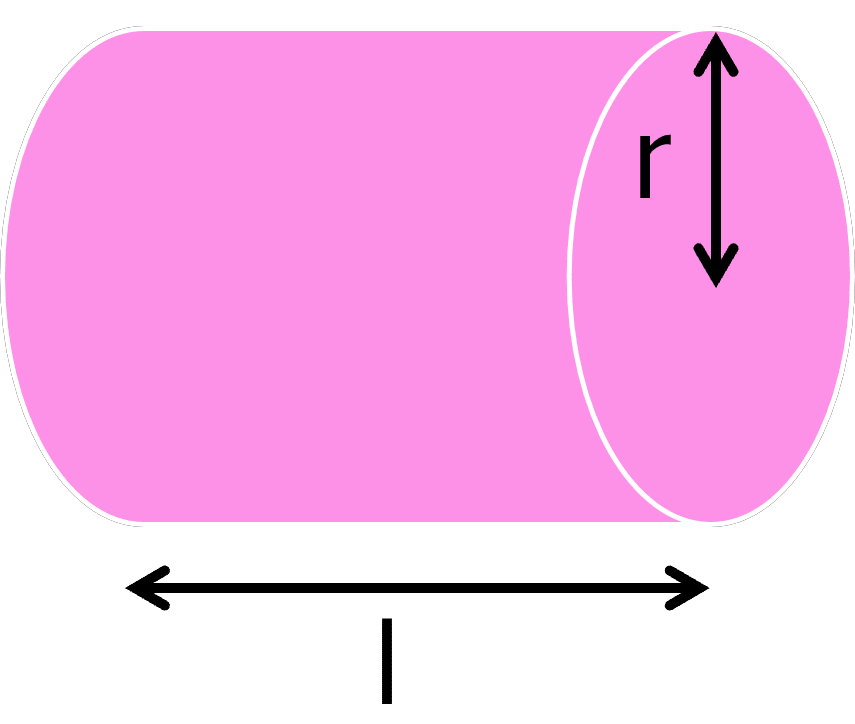
Cylinders

$V=\pi r^2 l$

$r=$ radius
$l=$ length

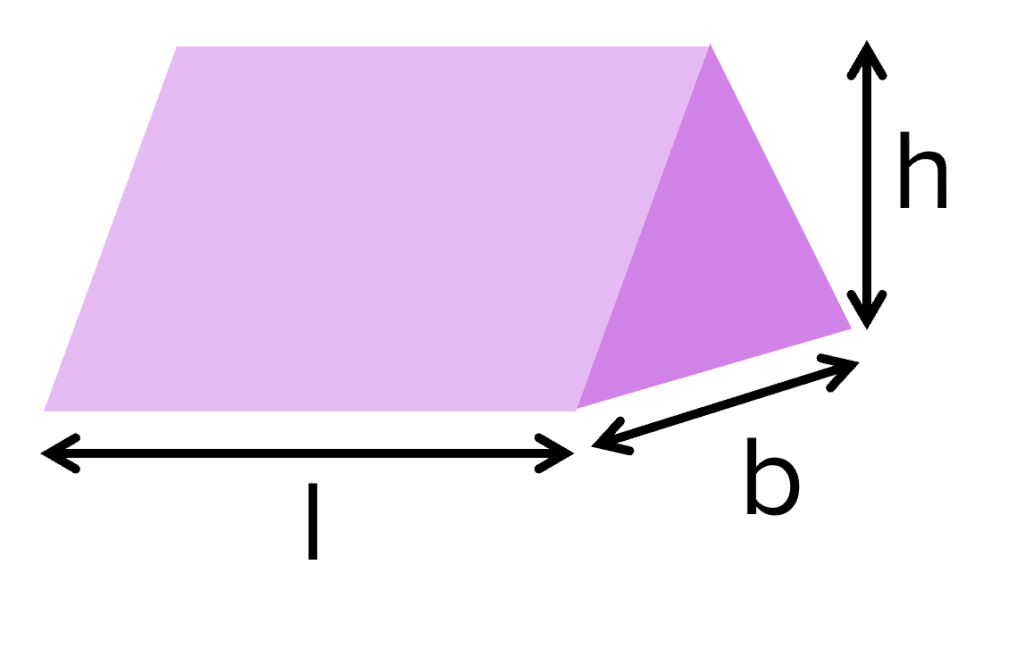
Triangular Prism

$V=\dfrac{1}{2}bhl$

$b=$ base
$h=$ height
$l=$ length

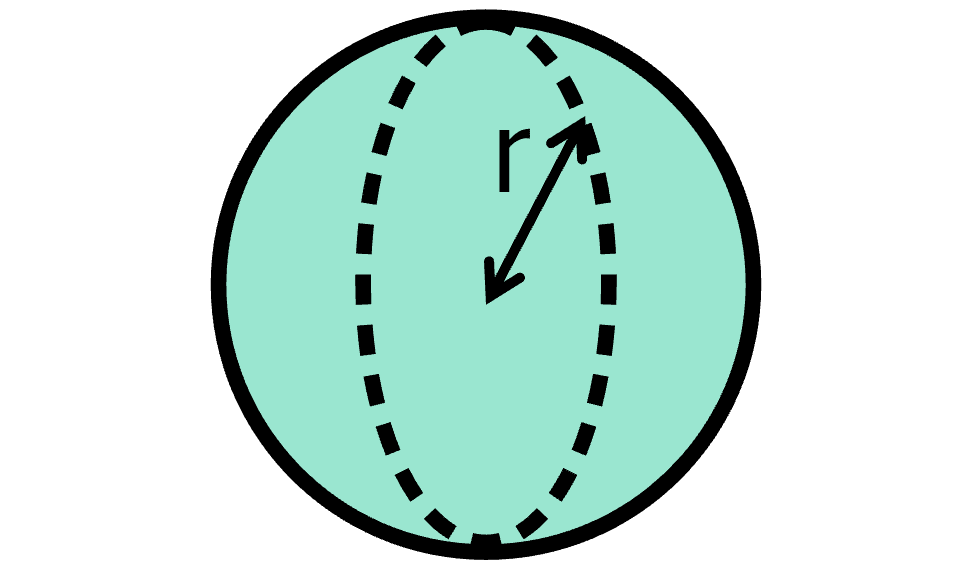
Sphere

$V=\dfrac{4}{3} \pi r^3$

$r=$ radius

Example 1: Calculating the Area of an Inhibition Zone.

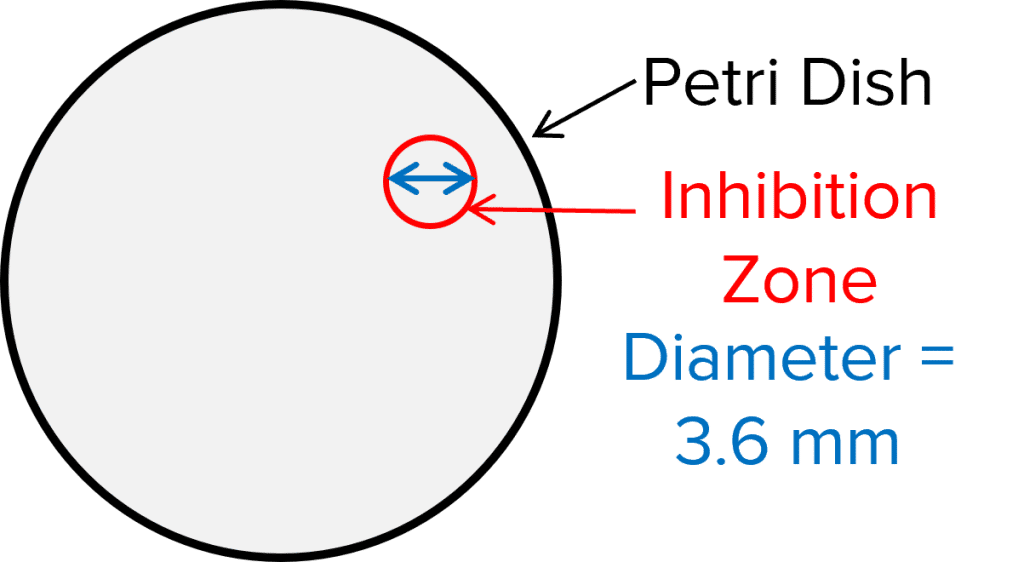
A biologist is performing an experiment on a new antibiotic drug. They measure a circular inhibition zone and find the diameter is $3.6 \text{ mm}$ .

Calculate the area of this inhibition zone.

[3 marks]

r=\dfrac{d}{2} = \dfrac{\textcolor{1c63ba}{3.6 \text{ mm}}}{2} = \textcolor{aa57ff}{\bold{1.8} \textbf{ mm}} \\ \bold{A=\pi r^2} = \pi \times (\textcolor{aa57ff}{1.8})^2 = \bold{10.2} \textbf{ mm}^2

Example 2: Calculating the Volume of Water Displaced

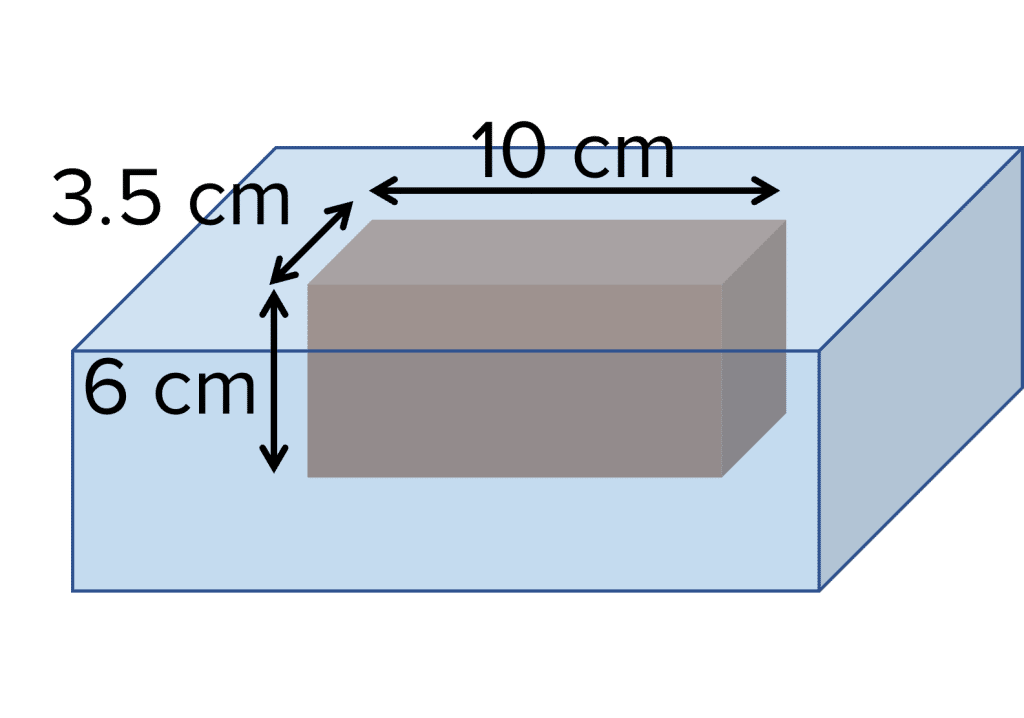
A wooden block with dimensions $\textcolor{f95d27}{10 \text{ cm}} \times \textcolor{f43364}{6 \text{ cm}} \times \textcolor{10a6f3}{3.5 \text{ cm}}$ is dropped into a container of water. Calculate the volume of water displaced by the wooden block.

[2 marks]

\text{volume of water displaced} \\ \begin{aligned} &= \text{volume of the block} \\ &= xyz \\ &= \textcolor{f95d27}{10} \times \textcolor{f43364}{6} \times \textcolor{10a6f3}{3.5} \\ &= \bold{210} \textbf{ cm}\bold{^3} \end{aligned}

Useful Formulae Example Questions

Question 1: Calculate the area of a square with sides of length $6 \text{ cm}$ .

[2 marks]

\begin{aligned} \bold{A} &= \bold{xy} \\ &= 6 \times 6 \\ &= \bold{36} \textbf{ cm}\bold{^2} \end{aligned}

MME Premium Laptop

Save your answers with

Gold Standard Education

Question 2: Calculate the volume of a sphere with radius $40 \text{ mm}$ .

[2 marks]

\begin{aligned} \bold{V} &= \bold{\dfrac{4}{3} \pi r^3} \\ &= \dfrac{4}{3} \times \pi \times 40^3 \\ &= \bold{268 \, 083} \textbf{ mm}\bold{^3} \end{aligned}

MME Premium Laptop

Save your answers with

Gold Standard Education

Question 3: Calculate the circumference of a circle with a diameter of $2 \text{ m}$ .

[2 marks]

\begin{aligned} \bold{C} &= \bold{\pi d} \\ &= \pi \times 2 \\ &= \bold{6.28} \textbf{ m} \end{aligned}

MME Premium Laptop

Save your answers with

Gold Standard Education

Gold Standard Education

£19.99 /month. Cancel anytime

Where next?

Previous GCSE Scientific Skills Topic

Rearranging Equations

GCSE Science Revision Home

Go back to the main topic list for GCSE Science

Next GCSE Scientific Skills Topic

Graphs and Data