Revise
Describing Motion
Describing Motion Revision
Describing Motion
When forces act on objects, there is motion. This motion has many different quantities such as displacement, velocity, acceleration and more. We can calculate these quantities with different equations.
Distance and Displacement
Distance is a scalar. This means it has magnitude but no direction. It simply means how far an object moves.
Displacement is a vector. This means it has both magnitude and direction. It measures both the distance an object moves in a straight line, and also the direction of this straight line.
For example, say you walk 10 \: \text{m} east, and then walk 10 \: \text{m} west. You are back at the same place you started, so you’re displacement is 0 \: \text{m}. But the distance you’ve travelled is 20 \: \text{m}.
Speed and Velocity
Speed
Speed is a scalar. It measures how fast an object is moving, and does not involve direction.
Some typical speeds are:
| Walking | \boldsymbol{1.5} \:\textbf{m/s} |
| Running | \boldsymbol{3} \: \textbf{m/s} |
| Cycling | \boldsymbol{6} \: \textbf{m/s} |
| Car | \boldsymbol{25} \: \textbf{m/s} |
| Speed of sound in air | \boldsymbol{330} \: \textbf{m/s} |
The speed at which someone can walk, run or cycle varies depending on age, fitness, terrain and the distance they travel. The speed of sound can also vary depending on what medium it’s in (air, vacuum etc).
To measure the speed of an object, you would need to use a stopwatch to time how long an object takes to travel a known distance. You would then use the following equation:
\textcolor{f21cc2}{\text{speed} = \dfrac{\text{distance}}{\text{time}} \:} \: \text{or} \: \textcolor{f21cc2}{\: v = \dfrac{s}{t}}
- speed in metres per second (\text{m/s})
- distance in metres (\text{m})
- time in seconds (\text{s}).
In real life, objects are rarely travelling at a completely constant speed. If the speed is not constant, then the speed you calculate will be the average speed.
Velocity
Velocity is a vector. It has both speed and direction.
An object can travel at a constant speed and at the same time, a changing velocity. This is because the speed may be constant but if the object’s direction is changing, then it’s velocity is changing.
Acceleration
Acceleration is when the velocity changes over a certain amount of time.
The average acceleration of an object can be calculated using the following equation:
\textcolor{00bfa8}{a = \dfrac{\Delta v}{t} }
- \textcolor{00bfa8}{a} is acceleration (metres per second squared, \text{m/s}^2)
- \textcolor{00bfa8}{\Delta v} is the change in velocity (metres per second, \text{m/s})
- \textcolor{00bfa8}{t} is the time (seconds, \text{s}).
When an object increases in speed, it is accelerating. When an object slows down, it is decelerating.
Uniform Acceleration
Uniform acceleration is another way of saying constant acceleration. It just means that the rate at which the velocity changes stays constant.
An example of uniform acceleration is gravitational acceleration, g. This is always constant at 9.8 \: \text{m/s}^2 for objects falling freely near the earths surface.
If an object is uniformly accelerating, we can use the following equation:
\textcolor{10a6f3}{v^2 - u^2 = 2as}
- \textcolor{10a6f3}{v} is the final velocity (\text{m/s})
- \textcolor{10a6f3}{u} is the initial velocity (\text{m/s})
- \textcolor{10a6f3}{a} is the acceleration (\text{m/s}^2)
- \textcolor{10a6f3}{s} is the distance (\text{m}).
Terminal Velocity
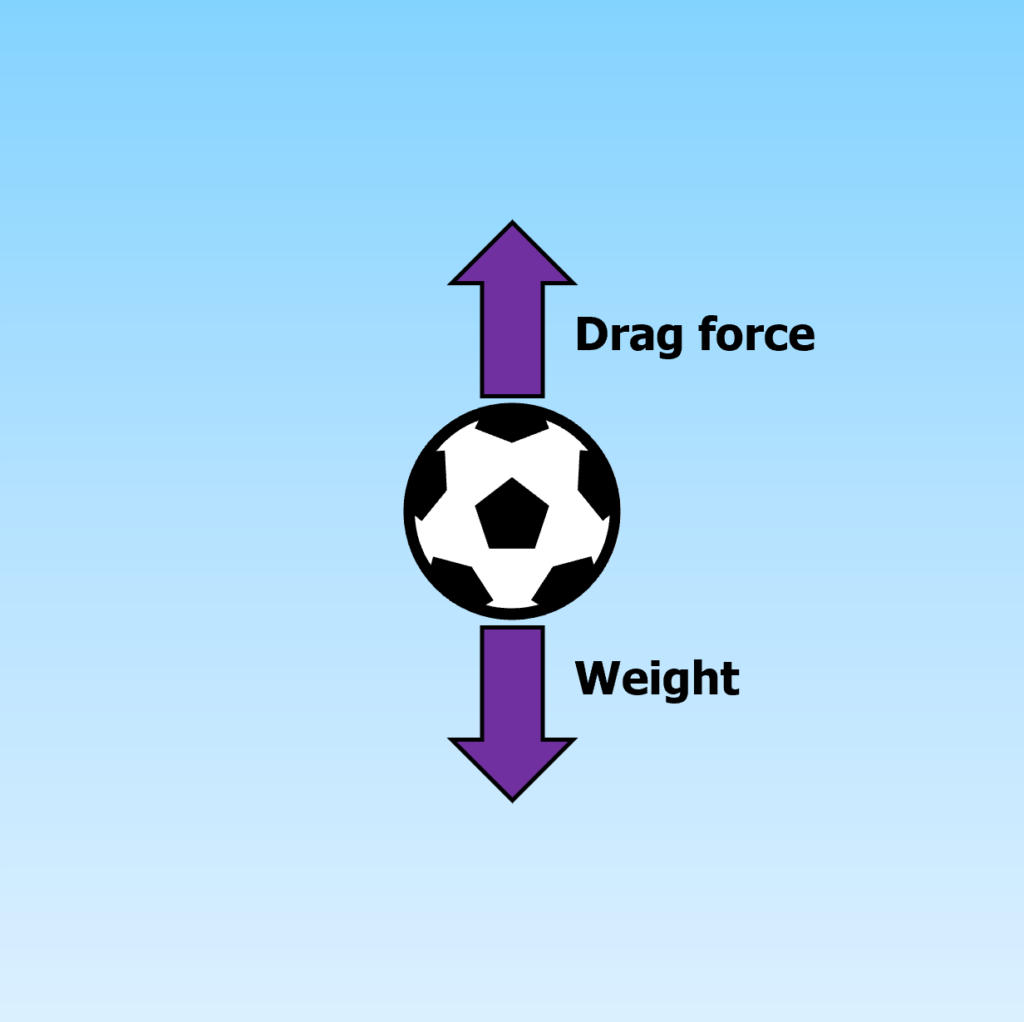
When an object is falling through a fluid (i.e air) vertically, there are two forces acting on the object: the object’s weight and drag.
The objects weight is due to gravity and acts downwards. The drag is the friction between the object and the fluid particles. An example of drag is air resistance. Air resistance opposes the force of gravity and slows the object down. This increases as the speed increases.
- As an object is dropped, it initially accelerates due to the gravitational force because this exceeds the drag force. There is a resultant force downwards.
- As the object’s speed increases, so does the drag.
- This continues until the drag force is equal to the force due to gravity. Because the forces are balanced, there is no resultant force and the object now moves at constant speed. This is the objects maximum speed and is called the terminal velocity.
Describing Motion Example Questions
Question 1: A car drives 500 \: \text{m} in 45 seconds. Calculate the speed of the car.
[2 marks]
\begin{aligned} \text{speed} &= \dfrac{\text{distance}}{\text{time}} \\ \\ \text{speed} &= \dfrac{500 \: \text{m}}{45 \: \text{s}} \\ \\ \textbf{speed} \: &\bold{=} \: \bold{11} \: \textbf{m/s} \end{aligned}
Question 2: A cyclist is travelling at a velocity of 6 \: \text{m/s} . They then pedal harder over a period of 10 \: \text{seconds} until their velocity is 8 \: \text{m/s} . Calculate the acceleration of the cyclist during this 10 \: \text{s} time period.
[3 marks]
\boldsymbol{a} \boldsymbol{= \dfrac{\Delta v}{t}} \\ \text{change in velocity} = 8 - 6 = \boldsymbol{2 \:} \textbf{m/s} \\ a = \dfrac{2 \: \text{m/s}}{10 \: \text{s}} \\ \boldsymbol{a} \boldsymbol{= 0.2} \: \textbf{m/s}^2
Question 3: Describe how a falling object reaches it’s terminal velocity.
[4 marks]
As the object is dropped, it initially accelerates due to it’s weight. Then, as the objects vertical speed increases, the drag force due to air resistance increases. This continues until the drag force is equal to the weight and the forces are balanced. There is no more acceleration and the object is moving uniformly at it’s maximum speed. This speed is called the terminal velocity.
