Pressure

Pressure at the Surface of a Liquid

A fluid is a substance that can flow and has no fixed shape, because the particles can move past each other. Liquids and gases are fluids.

Particles in fluid move around and collide with the surfaces of the container, and also with each other. These collisions exert a force on the surface of the container. Pressure is the force per unit area of a surface, so the particles are exerting a pressure on the container.

Pressure in a fluid causes a force at right angles (normal) to any surface. The pressure at a certain surface can be calculated using:

\textcolor{aa57ff}{p = \dfrac{F}{A}}

• \textcolor{aa57ff}{p} is the pressure in Pascals \left(\text{Pa}\right)
• \textcolor{aa57ff}{F} is the force normal to the surface in Newtons \left(\text{N}\right)
• \textcolor{aa57ff}{A} is the area of the surface in meters squared \left(\text{m}^2\right).

Pressure in a Column of Liquid

Density is a measure of how close the particles are in a substance. Density is uniform in liquids, meaning that it is the same everywhere in the liquid. However this is not true for gases.

We can relate density to pressure. If a substance is more dense, then there are more particles in the volume of space, and so there are more collisions between the particles. Collisions give rise to pressure, so a higher density means a higher pressure. 

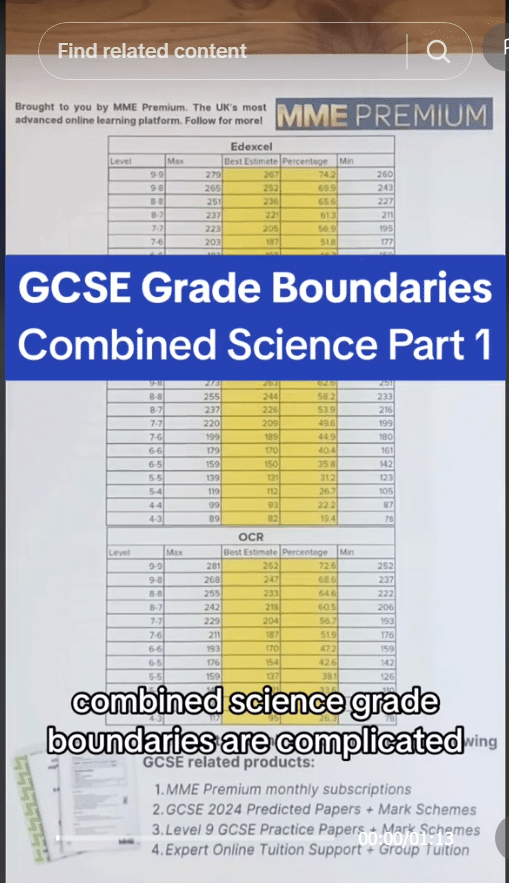
As the depth of a liquid increases, there is more particles above this depth. That means that the weight of these particles is on top of the liquid. This weight adds to the pressure in the liquid. Therefore as depth increases, so does the pressure.

 

To show this, let’s look at a cylinder filled with water. We have marked two points, A and B, on the cylinder. See how there is more liquid above point B than point A. Therefore there is more particles and more mass above point B than point A, adding to the pressure of the liquid. So the pressure at B is higher than at A.

Pressure at a certain depth can be calculated using the following equation:

\textcolor{f21cc2}{p = h \rho g}

• \textcolor{f21cc2}{p} is the pressure in Pascals \left(\text{Pa}\right)
• \textcolor{f21cc2}{h} is the height of the column in metres \left(\text{m}\right)
• \textcolor{f21cc2}{\rho} is the density of the liquid in kilogram per metres cubed \left(\text{kg/m}^3\right)
• \textcolor{f21cc2}{g} is the gravitational field strength in newtons per kilogram \left(\text{N/kg}\right)
• Remember that \textcolor{f21cc2}{g} on earth is 9.8 \text{N/kg}.

Upthrust

• When an object is submerged in a liquid, it experiences pressure due to the pressure in the liquid.
• Because pressure increases with depth, the bottom surface of this object will experience more pressure than the top surface.
• Because this bottom pressure is larger, there is a resultant force on the object upwards (remember that pressure and force are related). This resultant force upwards is called upthrust.
• The upthrust is equal to the weight of the water displaced by the object. This is just the weight of the water with the same volume as the object.

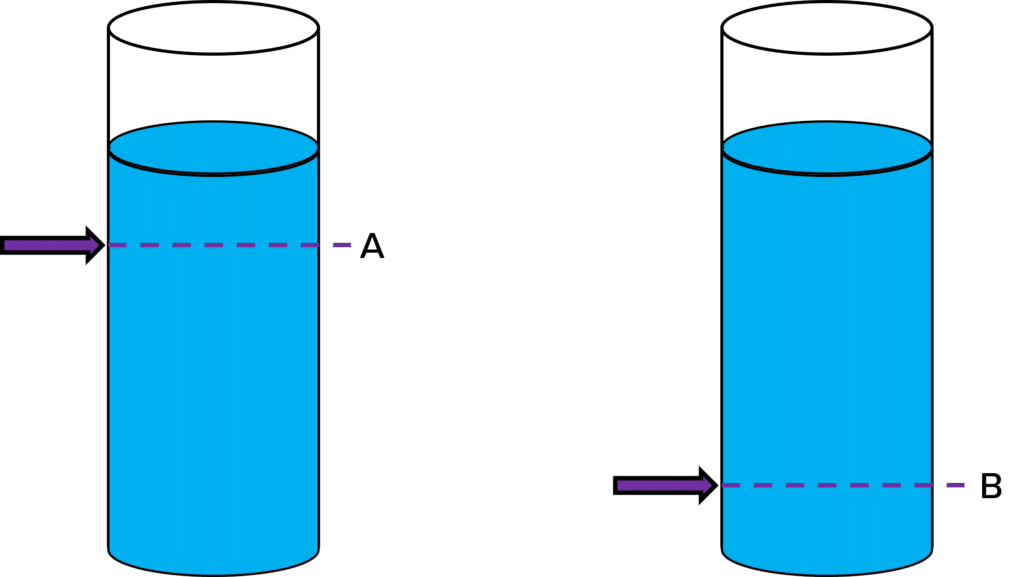
The balance of the forces will determine whether and object sinks or floats.

• If the upthrust is equal to or more than the weight of the object, the object floats because the forces are balanced.
• If the upthrust is less than the objects weight, the object sinks.

This is because floating or sinking depends on the density of the object. Upthrust is the weight of the displaced water. So if the density of this water is less than the object, then the weight of the water is less than the object as well. This means that the upthrust is less than the weight of the object. Hence the object would sink.

Atmospheric Pressure

There is a thin layer of air around the earth called the atmosphere. The atmosphere gets less dense as the height above earth (altitude) increases.

Air molecules collide with the surface of the atmosphere, creating atmospheric pressure. This atmospheric pressure decreases with increasing altitude. This is because as the altitude increases, the atmosphere is less dense. Therefore there are less particles to collide with the surface, so the pressure decreases.

Also, as the height increases, there is less air particles on top of the surface. This means less weight of air on top of the surface contributing to the pressure.  So this contribution to the pressure also decreases with altitude.