Moments, Levers and Gears
Moments, Levers and Gears Revision
Moments, Levers and Gears
Objects rotate due to the turning effect of the force that is acting on them. The magnitude of the turning effect depends on the force and the distance from the pivot that this force is applied. This turning effect is called a moment.
Moments
Force or multiple forces acting on an object about a pivot could cause the object to rotate. The moment of this force is its turning effect.
The moment of a force is given by the following equation:
\textcolor{aa57ff}{\text{Moment} = \text{Force} \times \text{distance}}
and you may see this written as:
\textcolor{aa57ff}{M = Fd}
- \textcolor{aa57ff}{M} is the moment of the force in Newton-metres, \left(\text{Nm}\right)
- \textcolor{aa57ff}{F} is the force in Newtons, \left(\text{N}\right)
- \textcolor{aa57ff}{d} is the perpendicular distance from the pivot to the line of action of the force in metres, \left(\text{m}\right).
Therefore if the force or distance from the pivot is large, the moment (turning effect) is larger.
For the largest possible moment, the force must be applied at a right angle to the object.
If an object is balanced and is stationary, this means that the total clockwise moment about the pivot is equal to the total anticlockwise moment. It will not turn.
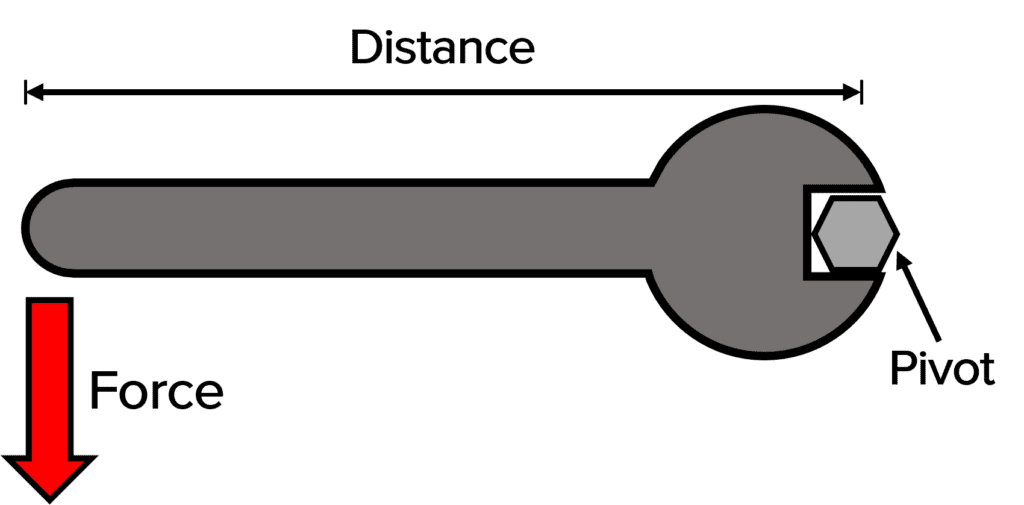
An example of a moment in action is when a spanner is used to turn a nut. The nut is the pivot, and the force is applied onto the handle of the spanner. A shorter spanner would mean a reduced turning effect, so it would require more force to turn.
Levers and Gears
Levers

If we want to decrease the force needed, then we can increase the distance from the pivot. Levers are used for this purpose.
By adding a long lever to a system, the distance from the pivot increases, and therefore less force is required for the turning effect.
An example of a lever is the long handles on a wheel barrow. These long handles increase the distance between you and the pivot (the wheel), meaning less force is required for the turning effect. This makes lifting the wheelbarrow a lot easier.

Gears
Gears are used to transmit the rotational effect of a force. The teeth of the gears in a gear system will interlock, meaning that one gear will cause the next to turn, but in the opposite direction.
The moment can be increased or decreased depending on the size of the gears. If a bigger gear transmits a force to a smaller gear, the moment is decreased, because in the smaller gear the distance to the pivot (centre of the gear) is less.
Example: Calculating Moments
Two masses are placed on a surface on a pivot. The surface is balanced. Calculate the distance 𝑥.
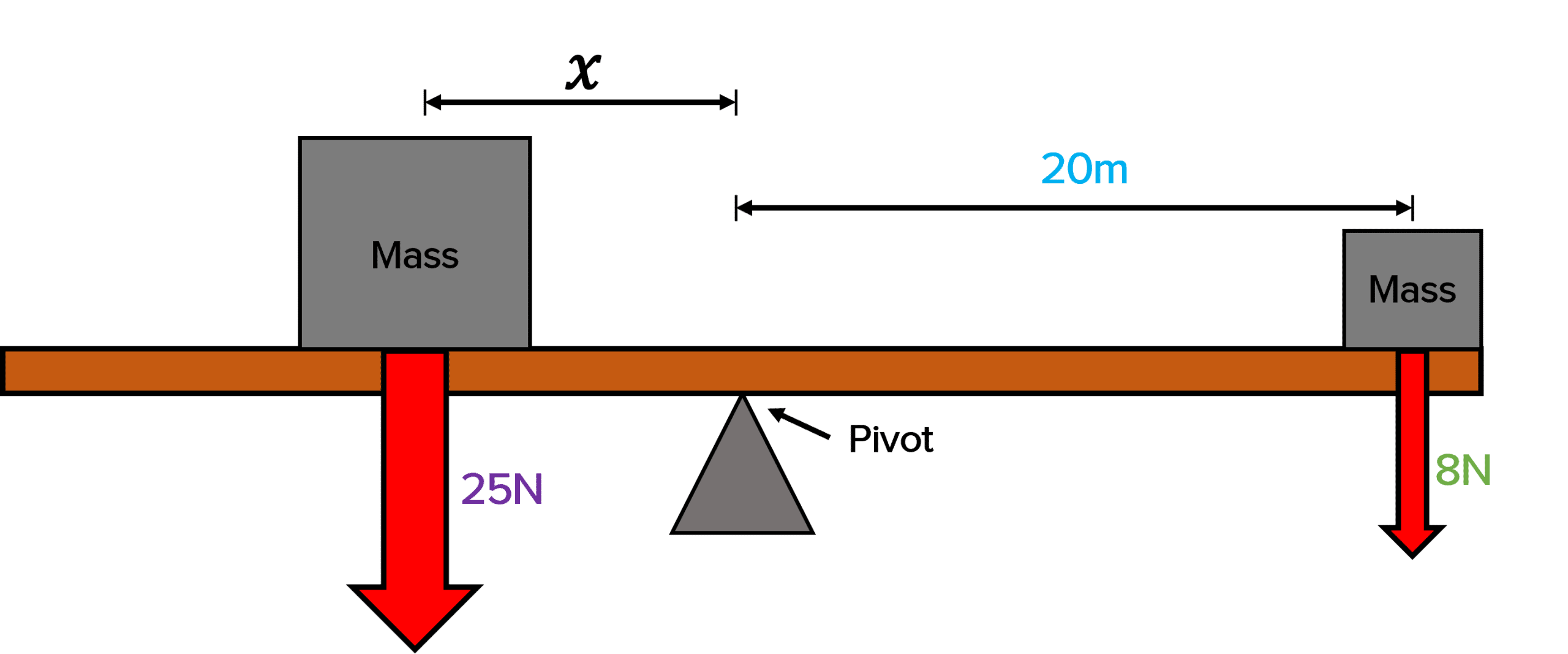
[3 marks]
The question says the surface is balanced. Therefore we know that the moments should be equal:
\text{Total anticlockwise moment = Total clockwise moment}
M = Fd
F_{1} \times d_{1} = F_{2} \times d_{2}
We can rearrange this equation:
d_1 = \dfrac{F_{2} \times d_{2}}{F_1}
x = d_1 = \dfrac{\textcolor{00d865}{8\: \text{N}} \times \textcolor{10a6f3}{20 \: \text{m}}}{\textcolor{aa57ff}{25 \: \text{N}}}
x = \dfrac{160 \: \text{Nm}}{\textcolor{aa57ff}{25 \: \text{N}}} = 6.4 \: \text{m}
Moments, Levers and Gears Example Questions
Question 1: A spanner is used to turn a nut. Calculate the moment of the system.
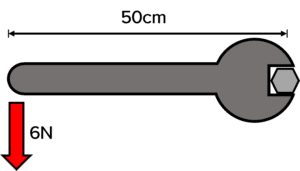
[2 marks]
\begin{aligned} M &= Fd \\ M &= 6 \: \text{N} \times 0.5 \: \text{m} \\ M &= \bold{3} \: \textbf{Nm} \end{aligned}
Question 2: A beam is being held up by a rope. The tension in the rope is 13 \: \text{N}. There is also a mass on the beam that weighs 45 \:\text{N}.
Calculate the moment of the system.
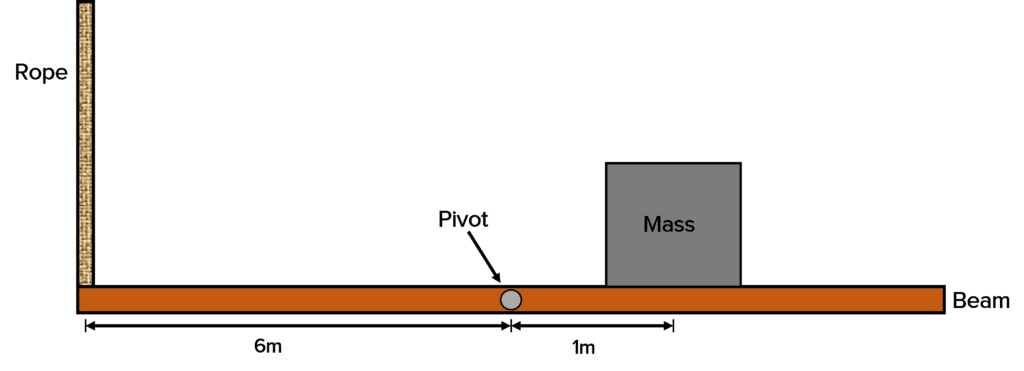
[3 marks]
The moments are not balanced because they are acting in the same direction (clockwise).
\begin {aligned} \text{Total moment} &= F_{1} \times d_{1} + F_{2} \times d_{2} \\ \text{Total moment} &= 13 \: \text{N }\times 6 \: \text{m} + 45 \: \text{N} \times 1 \: \text{m} \\ \textbf{Moment} &= \bold{123} \: \textbf{Nm} \end{aligned}
Question 3: Explain why it advantageous to use a gear system where a smaller gear transmits force to a larger gear.
[2 marks]
The larger gear has a larger radius, so the distance to the pivot is larger. The same force is transmitted and so the moment increases.
Moments, Levers and Gears Worksheet and Example Questions
Moments, Levers and Gears Questions
GCSEOfficial MME
MME Premium Membership
£19.99
/monthLearn an entire GCSE course for maths, English and science on the most comprehensive online learning platform. With revision explainer videos & notes, practice questions, topic tests and full mock exams for each topic on every course, it’s easy to Learn and Revise with the MME Learning Portal.
Sign Up Now
