Elasticity

Stretching, Bending and Compressing

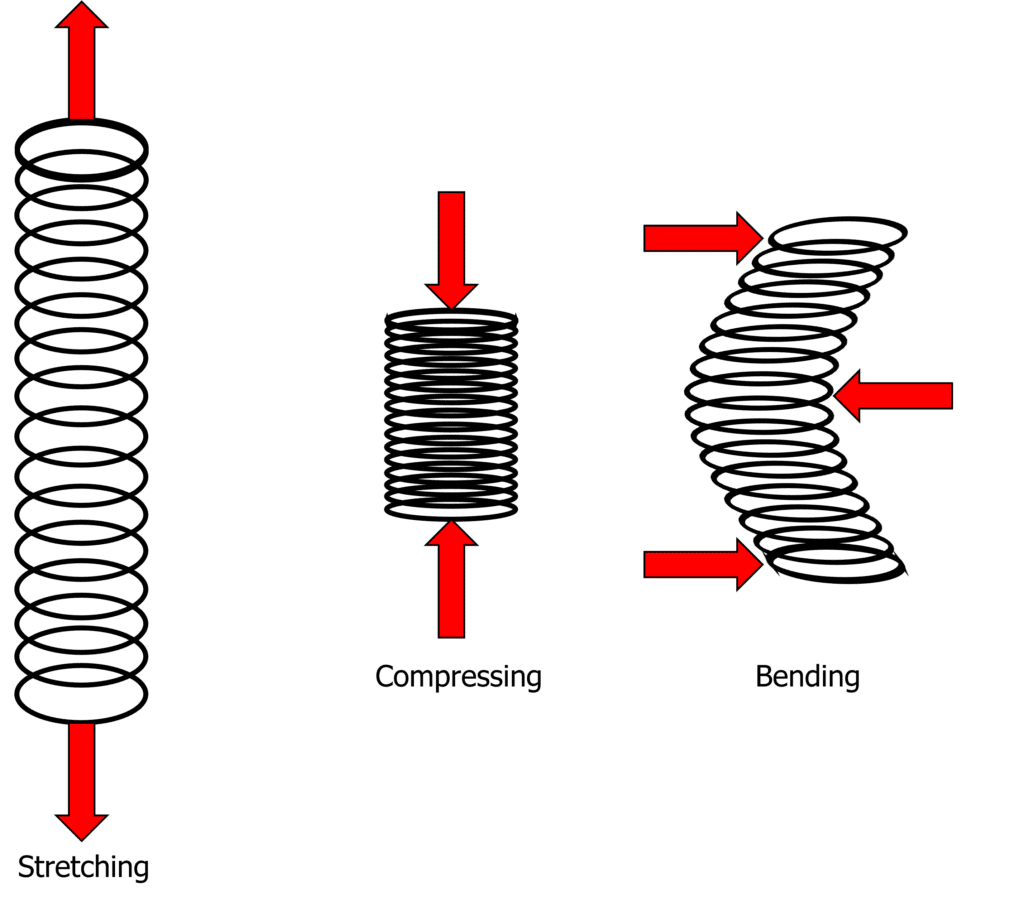
Applying force to an object will either stretch it, compress it or bend it. The area on the spring that the force is applied determines how the spring will move. Forces are applied as shown by the red arrows in the diagram.

In order to stretch, compress or bend an object, multiple forces need to be acting on it. If there was just one force acting on the object, then it would accelerate in the direction of that force.

For example, consider a spring hanging from a clamp stand with a mass hanging from the bottom. There is a contact force at the top of spring acting upwards and there is a weight force acting downwards. Therefore the spring is stretched.

Say the spring was removed from the clamp stand. There would be no contact force between the top of the spring and the clamp stand, so the spring would simply fall due to the force of it’s own weight.

Elastic/Inelastic Deformation

Elastic deformation is when an object has a force applied but can still go back to it’s original length and shape after the force has been removed.

Inelastic deformation is when the object with an applied force doesn’t return to it’s original length and shape when the force is removed.

Extension and Force

There is a relationship between the force applied to an elastic object and how much the object extends due to this force. 

The extension of an elastic object (i.e a spring) is directly proportional to the force applied to the object.

This can be written as a formula:

\textcolor{f21cc2}{\textbf{Force} = \textbf{spring constant} \times \textbf{extension}}

which can be written as:

\textcolor{f21cc2}{F = k \times e}

• \textcolor{f21cc2}{F} is the Force in Newtons, \left(\text{N}\right)
• \textcolor{f21cc2}{k} is the spring constant in Newtons per metre \left(\text{N/m}\right)
• \textcolor{f21cc2}{e} is the extension of the spring in metres \left(\text{m}\right).

\textcolor{f21cc2}{k}, the spring constant, is a measure how stiff a spring is. It’s different for different springs as it can depend on the material the spring is made from. A higher spring constant means the spring is stiffer.

The relationship also applies to compression. “Extension” is simply replaced by “Compression” in the equation.

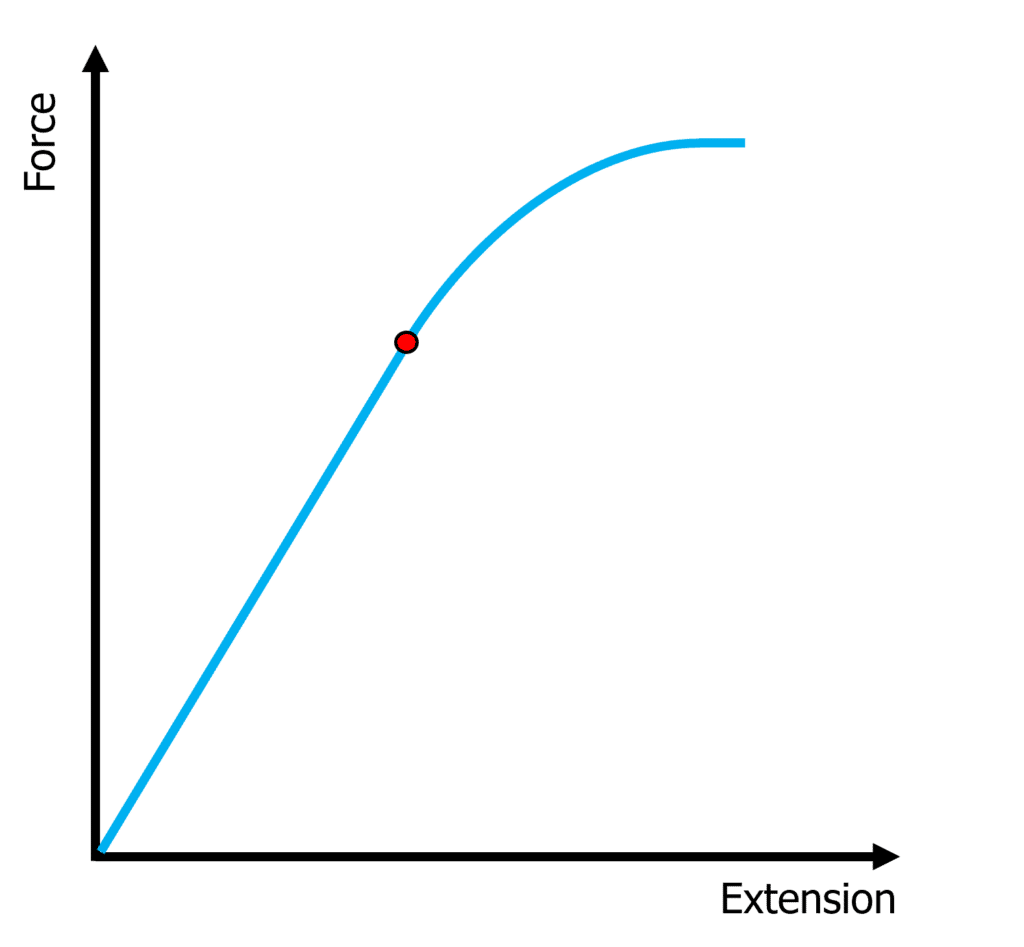
Limit of Proportionality

There are two things you must remember about this relationship. It is only valid if:

• The object is elastic.
• The limit of proportionality has not been exceeded.

The limit of proportionality is the maximum amount of force that can be applied before the force is no longer proportional to the extension. The point marked on the graph is where the limit of proportionality ends. Up until the point, the relationship between force and extension is linear and directly proportional. After this we can see the graph curves, because force is no longer proportional to extension. The relationship after this point is non-linear.

Elastic Potential Energy

When a spring is stretched or compressed, there is energy transfer involved. The force does work to change the shape of the spring, and this means energy is transferred to the elastic potential energy store of the spring. If the spring is elastically deformed, the work done by the force on the spring and the elastic potential energy stored are equal.

Elastic potential energy (or work done) can be calculated by using the following equation:

\textcolor{00bfa8}{E_{\text{e}} = \dfrac{1}{2} k e^2}

• \textcolor{00bfa8}{E_{\text{e}}} is the elastic potential energy of the spring in Joules \left(\text{J}\right)
• \textcolor{00bfa8}{k} is the spring constant in Newtons per metre \left(\text{N/m}\right)
• \textcolor{00bfa8}{e} is the extension (or compression) in metres \left(\text{m}\right).

Again, this equation is only valid for elastic objects up to the limit of proportionality.

Required Practical

Investigating the relationship between force and extension

This section details how you could use a practical set up to investigate the relationship between Force and Extension in a spring. It will involve using masses to stretch a spring, and recording it’s extension.

Doing the experiment

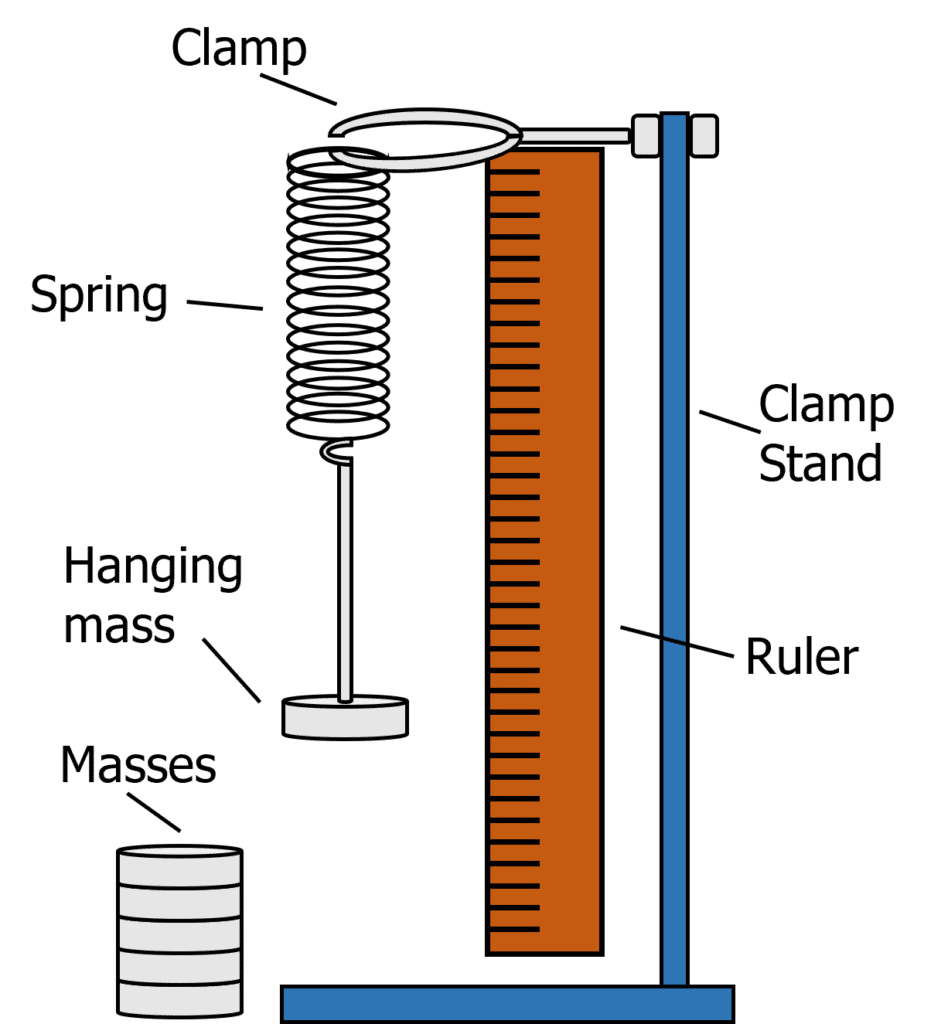
1. Set up the experiment as shown in the diagram.
2. Measure the original length of the spring with no load on it. Record this value or mark it on the meter ruler.
3. Next add a mass to the spring. Once the spring is stationary, measure the new length of the spring. Record the mass and new length. Calculate the extension by working out the difference between the original length of the spring and the new length of the spring.
4. Repeat this method, adding a mass to the spring each time. 
5. Calculate the force using the mass. To do this, we multiply the mass by 9.8. This is because \boldsymbol{W = mg}, and g = 9.8 \: \text{N/kg}.
6. Plot a graph of force against extension. It should look something like the force-extension graph below.

 

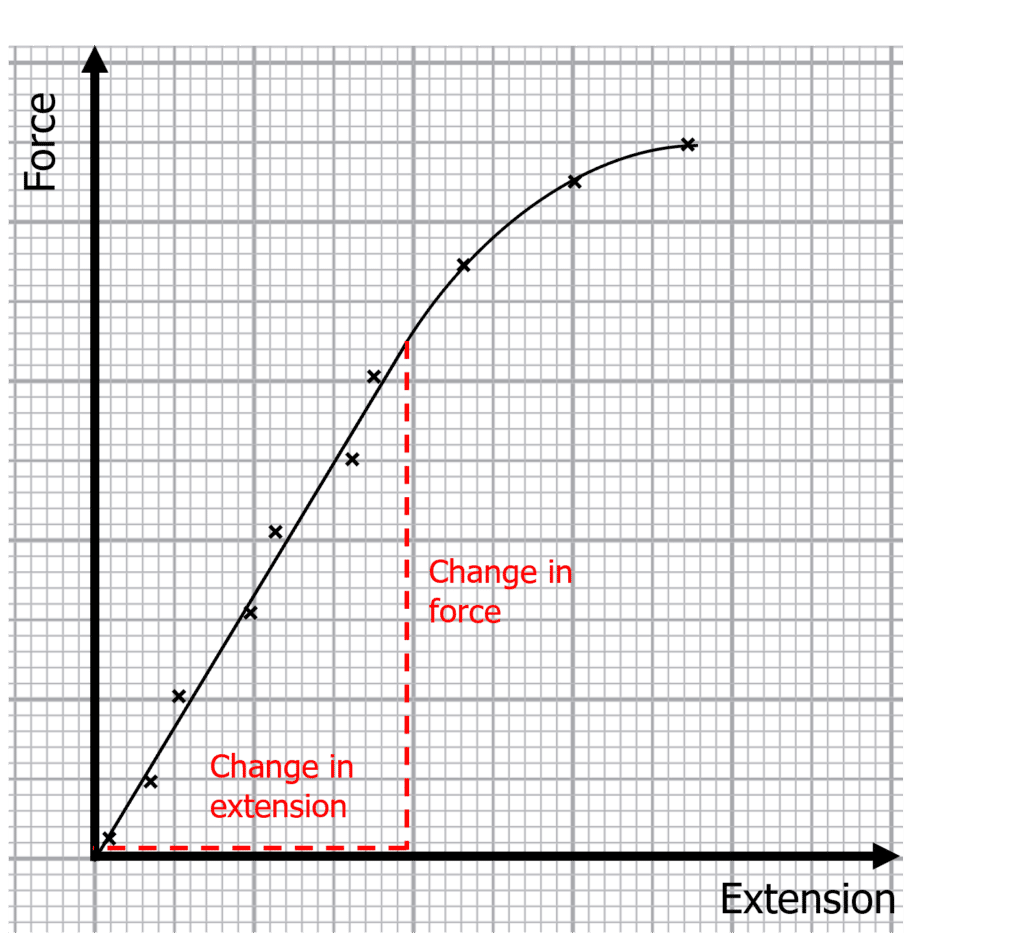
The graph can be used to calculate the spring constant. Using the equation e = \dfrac{F}{k}, we can calculate k by finding the gradient of the linear section of the graph. We only use the linear section because this is within the limit of proportionality.

k = \text{gradient} = \dfrac{\text{Change in force}}{\text{Change in extension}}