Titrations and Uncertainties
Titrations and Uncertainties Revision
Titrations and Uncertainties
A titration is an experiment that can be used to find the unknown concentration of a solution. An uncertainty is the estimated error when taking a measurement.
Titrations
Titrations are carried out to determine the concentration, \text{M}_{\text{r}}, or formula of an unknown compound. There are different types of titrations but we are going to focus on acid-base titrations.
Common Titrations
There are a few common titrations that you need to be able to recognise:
- \text{CH}_3\text{COOH}+\text{NaOH}\rightarrow\text{CH}_3\text{CO}_2^-\text{ Na}^++\text{H}_2\text{O}
- 2\text{HCl}+\text{Na}_2\text{CO}_3\rightarrow2\text{NaCl}+\text{CO}_2+\text{H}_2\text{O}
- \text{HCl}+\text{NaOH}\rightarrow\text{NaCl}+\text{H}_2\text{O}
- \text{H}_2\text{SO}_4+2\text{NaOH}\rightarrow\text{Na}_2\text{SO}_4+2\text{H}_2\text{O}
- \text{HCl}+\text{NaHCO}_3\rightarrow \text{NaCl}+\text{CO}_2+\text{H}_2\text{O}
Required Practical
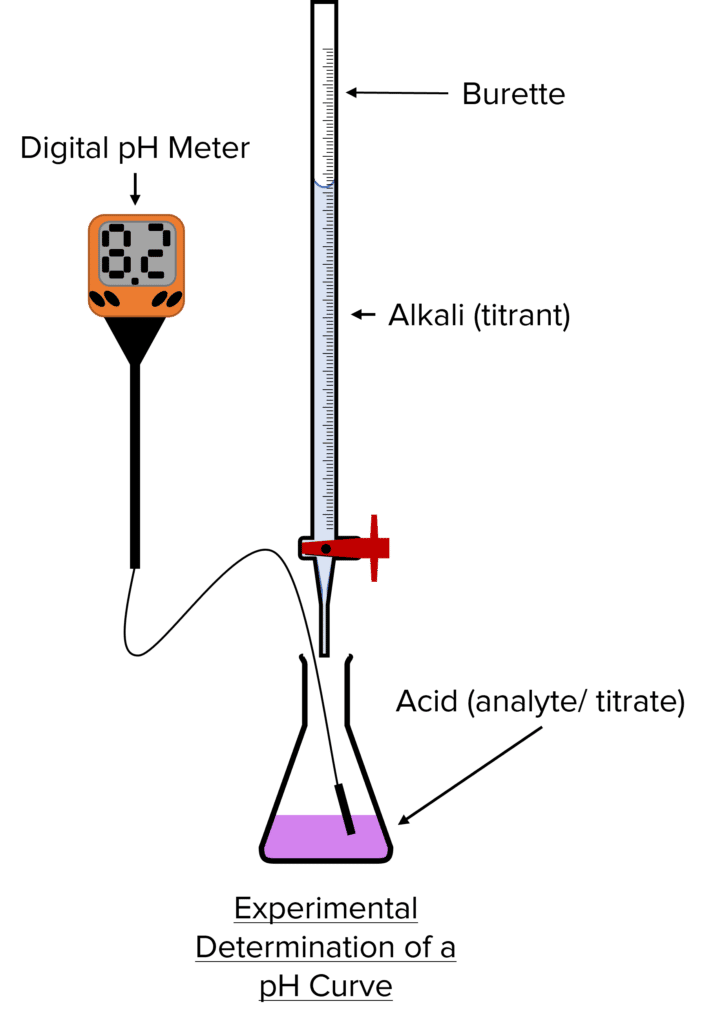

Carry Out a Simple Acid-base Titration
Method
- Rinse all equipment with distilled water.
- Using a pipette, add 25\text{ cm}^3 of alkali into a conical flask. Make sure to touch the walls of the flask with the pipette so that the correct amount is added.
- Add the acid solution to the burette and ensure the jet space of the burette is filled. Then note the reading on the burette.
- The jet space must be filled otherwise it could lead to errors in the readings, making them larger.
- Add a few drops of an indicator to the conical flask and place a white tile underneath.
- Make sure only a few drops are added since too much of it could affect the \text{pH} and the titration result.
- Add the acid to the alkali while mixing/ swirling the solution.
- Towards the endpoint, add the acid drop by drop until there is a colour change.
- Repeat the titration until you get at least 2 concordant results (within 0.20\text{ cm}^{-3} of each other) which can be used to calculate a mean.
Safety
The acids and alkalis are corrosive, so it is vital to wear goggles and gloves.
Titration Calculations
Generally, titrations can be calculated using the following steps.
- Work out the number of moles of the solution used to neutralise using the concentration equation.
- Find the ratio of moles between the the two solutions.
- Account for the volume of the sample used in the titrations. If a 25\text{ cm}^{-3} sample of a 250\text{ cm}^{-3} solution is used then the moles of the sample calculated through the titration will be \frac{1}{10}^{th} the amount of moles contained in the 250\text{ cm}^{-3} solution.
- Using the moles now calculated, work out the concentration.
Example: A \textcolor{#00bfa8}{25.0\text{ cm}^3} sample of lithium hydroxide solution of unknown concentration is neutralised by \textcolor{#f21cc2}{12.5\text{ cm}^3} of \textcolor{#a233ff}{0.15\text{ mol dm}^{-3}} sulfuric acid.
Calculate the concentration of the lithium hydroxide solution.
2\text{LiOH}_{\left(\text{aq}\right)}+\text{H}_2\text{SO}_{4\left(\text{aq}\right)}\rightarrow\text{Li}_2\text{SO}_{4\left(\text{aq}\right)}+2\text{H}_2\text{O}_{\left(\text{l}\right)}
\text{Moles of H}_2\text{SO}_4=\textcolor{#a233ff}{0.15}\times\dfrac{\textcolor{#f21cc2}{12.5}}{1000}=\textcolor{#008d65}{1.875\times10^{-3}\text{ mol}}
\text{Ratio of LiOH}\text{ to H}_2\text{SO}_4=\textcolor{#008d65}{2:1}
\text{Moles of LiOH}= 1.875\times10^{-3}\times2=\textcolor{#008d65}{3.75\times10^{-3}\text{ mol}}
\begin{aligned}\text{Concentration}&=\dfrac{\text{Moles}}{\text{Volume}}\\&=\dfrac{3.75\times10^{-3}}{25\div1000}\\&=\textcolor{#008d65}{0.15\text{ mol dm}^{-3}}\end{aligned}
Back Titration Calculations
Back titrations are a type of titration where instead of directly measuring the concentration of an unknown compound, the concentration is measured by finding out the excess amount of the known concentration.
Example: \textcolor{#00bfa8}{900\text{ mg}} of impure calcium carbonate tablet was crushed. \textcolor{#f21cc2}{50.0\text{ cm}^3} of \textcolor{#a233ff}{1.00\text{ mol dm}^{-3}} hydrochloric acid, an excess, was then added. After the tablet had reacted, the mixture was transferred to a volumetric flask. The volume was made up to \textcolor{#eb6517}{100\text{ cm}^3} with distilled water.
\textcolor{#cc0000}{20.0\text{ cm}^3} of this solution was titrated with \textcolor{#0040ff}{23.3\text{ cm}^3} of \textcolor{#b3b300}{0.300\text{ mol dm}^{-3}} of a sodium hydroxide solution.
Calculate the percentage of \text{CaCO}_3 by mass in the tablet.
Step 1: Calculate the moles of \text{HCl} used to dissolve the tablet.
\text{NaOH}+\text{HCl}\rightarrow\text{NaCl}+\text{H}_2\text{O}
\text{Moles of NaOH}= \text{Concentration}\times\text{Volume}= \textcolor{#b3b300}{0.300}\times\dfrac{\textcolor{#0040ff}{23.3}}{1000}=\textcolor{#008d65}{6.99\times10^{-3}\text{ mol}}
\text{Ratio of NaOH} to \text{HCl}=1:1
\text{Moles of HCl}=\textcolor{#008d65}{6.99\times10^{-3}\text{ mol}}
Step 2: Calculate the moles of \text{HCl} that reacted with the \text{CaCO}_3.
\text{Moles of HCl in the }\textcolor{#eb6517}{100\text{ cm}^3}\text{ solution}=6.99\times10^{-3}\times\frac{\textcolor{#cc0000}{20.0}}{\textcolor{#eb6517}{100}}=\textcolor{#008d65}{0.0350\text{ mol}}
Step 3: Calculate the Mass of \text{CaCO}_3 in the tablet.
\text{Moles of HCl Original}=\dfrac{\textcolor{#f21cc2}{50.0}}{1000}\times\textcolor{#a233ff}{1.00}=\textcolor{#008d65}{0.050\text{ mol}}
\text{Moles of HCl reacted with CaCO}_3=0.050-0.0350=\textcolor{#008d65}{0.0150\text{ mol}}
\text{CaCO}_{3\left(\text{aq}\right)}+\text{2HCl}_{\left(\text{aq}\right)}\rightarrow\text{CaCl}_{2\left(\text{aq}\right)}+\text{CO}_{2\left(\text{g}\right)}+\text{H}_2\text{O}_{\left(\text{l}\right)}
\text{Ratio of HCl} to \text{CaCO}_3=\textcolor{#008d65}{2:1}
\text{Moles of CaCO}_3=0.0150\div2=\textcolor{#008d65}{0.00750\text{ mol}}
\text{Mass of CaCO}_3=0.00750\times\left(40+12+\left[3\times16\right]\right)=\textcolor{#008d65}{0.750\text{ g}}
Step 4: Calculate the percentage by mass of \text{CaCO}_3 in the tablet.
\text{Percentage by mass}=\dfrac{0.750}{\textcolor{#00bfa8}{0.9}}\times100=\textcolor{#008d65}{83\%}
Calculating Uncertainties
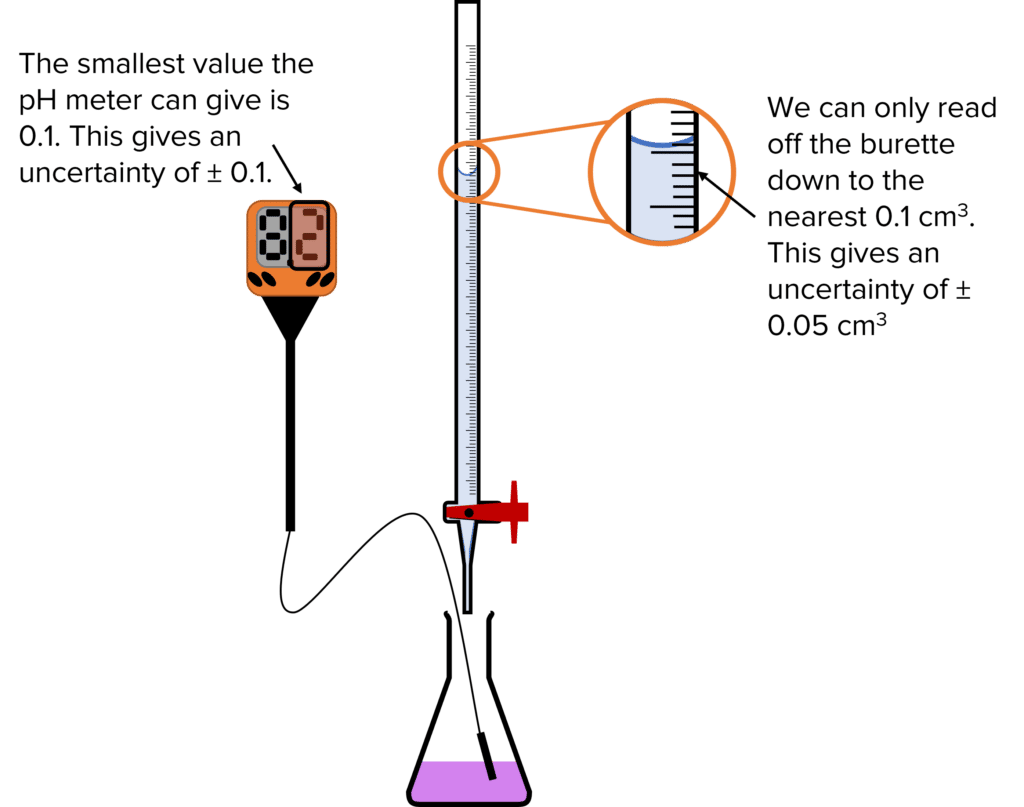

When carrying out titrations (or any experiment), each piece of equipment will have an associated uncertainty. The following are the usual uncertainties for pieces of equipment used in titrations, however, a question could use a different value.
- Burette: \pm 0.15\text{ cm}^3 – This value is three times the uncertainty of the burette. One uncertainty is taken from the 0 reading at the start of the titration. Another is taken from the final reading of the the burette. The third uncertainty is added to account for the fact that it is impossible to add exactly the right amount of titrant to reach the end point (known as end point uncertainty).
- 25\text{ cm}^3 Pipette: \pm 0.1\text{ cm}^3
- Volumetric Flask: \pm\text{ 0.1 cm}^3
- Balance: \pm\text{0.001 g}
\% \text{uncertainty}=\pm\dfrac{\text{uncertainty}}{\text{measurement made in apparatus}}\times100
Example: A student carries out a titration and obtains the following data:

During the experiment, the student used a burette to add sodium hydroxide to hydrochloric acid. The uncertainty of the burette is \pm 0.15\text{ cm}^3.
We can calculate the percentage uncertainty of the mean titre volume from the results. It is important to remember that uncertainties are always quoted to 1 significant figure. Remember that when calculating the mean titre volume, we only use the concordant results (results with 0.20\text{ cm}^3 of each other).
\text{Mean titre volume}=\dfrac{32.15+32.10}{2}=32.13\text{ cm}^3
\begin{aligned}\%\text{uncertainty}&=\pm\dfrac{\text{uncertainty}}{\text{measurement made in apparatus}}\times100\\ &=\dfrac{0.15}{32.13}\times100\\ &=\pm 0.5\%\end{aligned}
Sometimes, when using titrations to find out known information, such as the \text{M}_r of a compound, we can find that the value obtained is different from the actual value. For example, calculating that the concentration of a \text{M}_r is 125 when the actual value is 150.
By comparing the percentage uncertainty and the percentage difference between the actual and recorded values, we can find out more about the reason why values obtained in an experiment may be different to real values. We do this by finding the percentage difference between the real value and the calculated value.
- If the percentage difference is less than the percentage uncertainty, then the difference in values obtained are due to the equipment used.
- If the percentage difference is greater than the percentage difference, then the difference in values obtained are not due to the equipment used and may be due to other errors.
Note: To calculate total percentage uncertainty the percentage uncertainty of each piece of equipment is added together.
Reducing Uncertainties
When carrying out any experiment, each piece of equipment will have an associated uncertainty. However, it is always beneficial to use apparatus with lower uncertainties and finer resolutions.
Examples of this include:
- Using a pipette instead of a measuring cylinder
- Using a balance with more decimal places
Another way to reduce uncertainty is by using larger volumes or masses since small readings have higher experimental uncertainties. Using higher masses also means that the fixed errors of equipment will be a smaller percentage of the final reading. In a titration, we use a larger titre to reduce uncertainty. To do this, we can increase the volume or concentration of the substance in the conical flask.
Titrations and Uncertainties Example Questions
Question 1: A solution is made by dissolving 0.50\text{ g} of solid sodium hydroxide in 250\text{ cm}^3 of water. To neutralise a 45.0\text{ cm}^3 sample of ethanoic acid (\text{CH}_3\text{COOH}) with unknown concentration, 31.6\text{ cm}^3 of the sodium hydroxide solution is needed.
Calculate the concentration of the ethanoic acid.
[4 marks]
\text{Moles of NaOH in }25\text{ cm}^3=\dfrac{0.50}{40}=0.0125
\text{Concentration of NaOH solution in }250\text{ cm}^3=\dfrac{0.0125}{250\div1000}=0.05\text{ mol dm}^{-3}
\text{NaOH}+\text{CH}_3\text{COOH}\rightarrow\text{CH}_3\text{COO}^-\text{Na}^++\text{H}_2\text{O}
\text{Moles of NaOH used in neutralisation}=\dfrac{31.6}{1000}\times0.05=1.58\times10^{-3}
Ratio of \text{NaOH} to \text{CH}_3\text{COOH} = 1:1
\text{Moles of CH}_3\text{COOH}=1.58\times10^{-3}
\text{Concentration of CH}_3\text{COOH}=\dfrac{1.58\times10^{-3}}{45\div1000}=0.0351\text{ mol dm}^{-3}
Question 2: 1.50\text{ g} of impure \text{MgCO}_3reacts with 75.0\text{ cm}^3 of 0.5\text{ mol dm}^{-3} of hydrochloric acid. Some of the hydrochloric acid is unreacted.
For a complete reaction, 23.8\text{ cm}^3 of 0.5\text{ mol dm}^{-3} of sodium hydroxide reacts with the unreacted hydrochloric acid.
Calculate the percentage by mass of magnesium carbonate in the impure sample.
[6 marks]
\text{Moles of HCl added} = \dfrac{75}{1000}\times0.5=3.75\times10^{-2}
\text{Moles of NaOH to neutralise}=\dfrac{23.8}{1000}\times0.5=0.0119
\text{NaOH}+\text{HCl}\rightarrow\text{NaCl}+\text{H}_2\text{O}
\text{Moles of HCl neutralised}= 0.0119
\text{Moles of HCl reacted}=3.75\times10^{-2}-0.0119=0.0256\text{ mol}
\text{MgCO}_3+2\text{HCl}\rightarrow\text{MgCl}_2+\text{H}_2\text{O}+\text{CO}_2
\text{Moles of MgCO}_3=0.0256\div2=0.0128\text{ mol}
\text{Mass}=0.0128\times84.3=1.08\text{ g}
\%\text{ MgCO}_3\text{ in sample}=\dfrac{1.08}{1.5}\times100=72\%
Question 3: A student carries out a titration to determine the concentration of some hydrochloric acid. The student uses a pipette to measure out 25.0\text{ cm}^3 of \text{Na}_2\text{CO}_3 to use in the titration. The results are as follows.

The volumes were measured with a pipette and a burette.
- The pipette had an uncertainty of \pm0.04 \text{cm}^3 in the volume measured.
- The burette had an uncertainty of \pm0.05\text{ cm}^3 in the volume measured.
Determine which piece of equipment has the greatest percentage uncertainty.
[3 marks]
\text{Mean/average titre}= \dfrac{23.6+23.65}{2}=23.63
\text{Uncertainty of pipette}=\dfrac{0.04}{25}\times100=0.16\%
\text{Uncertainty of burette}=\dfrac{0.05\times3}{23.63}\times100+0.63\%
The percentage uncertainty for the burette is greater.
You May Also Like...

MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.