Revise
Concentrations of Solutions
Concentrations of Solutions Revision
Concentrations of Solutions
The vast majority of chemical reactions take place in solution. The concentration of a solution is a measure of the amount of a substance that it contains, and is measured in \text{g/dm}^3 (grams per decimeter cubed). Concentration is calculated as a ratio of the mass of a substance to the volume of the liquid used to dissolve it.
Conservation of Concentrations
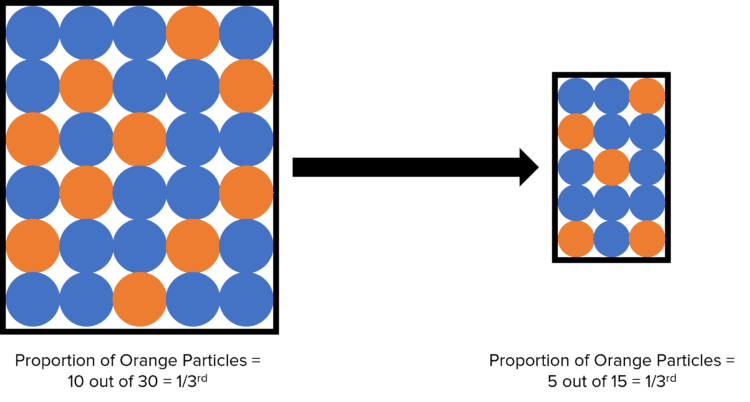
Provided the number of particles of the substance in solution is not changed (i.e. no solute or solvent is added or removed) then the concentration of a solution will remain constant across volumes. For example, if a 25\text{ mL} sample of a 100\text{ mL} sodium hydroxide solution with a 0.5 \text{ g/dm}^3 was taken, the concentration of this sample would also be 0.5\text{ g/dm}^3. This is because the ratio of sodium chloride molecules in the both solutions is the same.
Concentration Calculations
Concentrations are calculated using the following formula:
\text{Concentration}=\frac{\text{Mass of Solute in Solution (g)}}{\text{Volume of Solvent (dm)}}
This gives us \text{g/dm}^3 as the unit for concentration. The unit of volume used, the decimeter \left(\text{dm}\right) may be one that seems unfamiliar. The decimeter is an extremely common unit in chemistry. 1 \text{ dm}^3 is equal to 1000 \text{ cm}^3. To convert from \text{cm}^3 to \text{dm}^3 we divide the former by 1000:
\text{Volume in dm}^3=\frac{\text{Volume in cm}^3}{1000}
When talking about solutions, there are four important definitions to know:
1. Solute: The solid substance which is dissolved in a solution
2. Solvent: The liquid in which a substance is dissolved to form a solution
3. Soluble: A compound that can be dissolved in a given solution
4. Insoluble: A solution that can’t be dissolved in a given solution
To illustrate this, take solid copper sulfate dissolved in water to form a solution. The solid copper sulfate has been dissolved and so this is the solute. The water is the liquid used to dissolve the copper sulfate and so this is the solvent.
Water is the most common solvent used to create solutions of ionic compounds. When solutions are created using water as the solvent, these solutions are said to be aqueous. Covalent compounds are often dissolved in organic solvents such as hexane.
Molar Concentrations
Though concentrations can be measured in \text{g/dm}^3, it is more common in chemistry to measure them in \text{mol/dm}^3. When reporting the concentrations of solutions in scientific papers, it is almost always \text{mol/dm}^3 that is used. Calculating molar concentrations of solutions works in much the same was as the mass concentration given above:
\text{Concentration of Solution}=\frac{\text{Moles of Solute}}{\text{Volume of Solvent}}
Often the amount of solute will not be given in moles however. It will typically still be given in grams. Before calculating molar concentrations, the mass of the solute must be converted to moles. The molar concentration of a substance will often be smaller from the mass concentration, as the number of moles of solute is typically smaller than the mass of the solute.
Example 1: Calculating Concentration
A student prepares a solution of copper sulfate \left(\text{CuSO}_4, \text{M}_r =\textcolor{#00bfa8}{160}\right) for an experiment. They dissolve \textcolor{#f21cc2}{7.5\text{ g}} of solid copper sulfate in \textcolor{#327399}{15\text{ dm}^3} of water. Calculate the concentration of this solution in \text{mol/dm}^3:
[2 marks]
First we have to convert from mass to moles:
\text{Moles of}\text{ Copper Sulfate}=\frac{\text{Mass of Copper Sulfate}}{\text{M}_r \text{ Copper Sulfate}}\\ \, \\=\frac{\textcolor{#f21cc2}{7.5}}{\textcolor{#00bfa8}{160}}\\ \, \\ =\textcolor{#008d65}{0.046\text{ mol}}
This done, we can calculate the concentration of the solution:
\text{Concentration of}\text{ Copper Sulfate Solution}= \frac{\text{Moles of Copper Sulfate Dissolved}}{\text{Volume of Water Used}}\\ \, \\ =\frac{0.046}{\textcolor{#327399}{15}}\\ \, \\=\textcolor{#008d65}{0.003\text{ mol/dm}^3}
Example 2: Calculating Mass from Concentration
In a different experiment, a student is required to make up a \textcolor{#00bfa8}{25\text{ dm}^3} solution of sodium chloride with a concentration of \textcolor{#f21cc2}{0.7 \text{ g/dm}^3}. Calculate the mass of sodium chloride needed for this solution:
[2 marks]
\text{Concentration of Sodium}\text{ Chloride Solution} = \frac{\text{Mass of Sodium Chloride Dissolved}}{\text{Volume of Water Used}}
\text{Mass of}\text{ Sodium Chloride}= \text{Volume of Water Used} \times \text{Concentration of}\text{ Sodium Chloride}\text{Solution}\\ \, \\=\textcolor{#00bfa8}{25} \times \textcolor{#f21cc2}{0.7} \\ \, \\= \textcolor{#008d65}{17.5 \text{ g}}
Example 3: Calculating Concentrations with Unit Conversion
A student prepares a solution of hydrochloric acid by dissolving \textcolor{#00bfa8}{3.55\text{ g}} of solid hydrochloric acid in \textcolor{#f21cc2}{250\text{ cm}^3} of water. Calculate the concentration of this solution in \text{g/dm}^3:
[3 marks]
In this case, the volume of solvent has been given in \text{cm}^3. As such, it will need to be converted in to \text{dm}^3 before the concentration can be calculated:
\text{Volume in dm}^3 =\frac{\text{Volume in cm}^3}{1000}\\ \, \\=\frac{\textcolor{#f21cc2}{250}}{1000}\\ \, \\=\textcolor{#008d65}{0.25\text{ dm}^3}
Once the conversion is done, the concentration of the solution can be calculated:
\text{Concentration of}\text{ Hydrochloric Acid}=\frac{\textcolor{#00bfa8}{3.55}}{0.25}=\textcolor{#008d65}{14.2\text{ g/dm}^3}
Concentrations of Solutions Example Questions
Question 1: Define the terms solute and solvent.
[2 marks]
Solute: (The/A) solid substance that has been dissolved in solution.
Solvent: (The/A) liquid substance that has been used to dissolve a solid to form a solution.
Question 2: A student prepares a solution of magnesium hydroxide solution using 9.00\text{ g} of magnesium hydroxide and 25\text{ dm}^3 of water. Calculate the concentration of this solution in \text{g/dm}^3.
[1 mark]
\text{Concentration of Magnesium Hydroxide}=\frac{\text{Mass of Magnesium Hydroxide}}{\text{Volume of Water}}
\text{Concentration of Magnesium Hydroxide}=\frac{9.00}{25}=\underline{0.36\text{ g/dm}^3}
(if molar calculation has been preformed a concentration of \underline{0.009\text{ mol/dm}^3} gains 1 mark)
Question 3: A 2.5\text{ g/dm}^3 solution of ammonia is prepared using 3.5\text{ dm}^3 of water. Calculate the mass of ammonia in the solution:
[2 marks]
\text{Concentration of Ammonia}=\frac{\text{Mass of Ammonia}}{\text{Volume of Water}}
\begin{aligned}\text{Mass of Ammonia} &= \text{Concentration of Ammonia} \times \text{Mass of Ammonia}\\ &=2.5\times3.5\\ &=\underline{8.75\text{ g}}\end{aligned}
(One mark for correct rearrangement. One mark for correct answer.)
Question 4: A solution of rubidium chloride \left(\text{RbCl}\right) is prepared by dissolving 0.004\text{ mol} of \text{RbCl} in 1.5\text{ dm}^3 of water. Calculate the concentration of this solution (to 3 d.p.). Give the unit of concentration.
[2 marks]
\begin{aligned}\text{Concentration of RbCl} &= \frac{\text{Moles of RbCl}}{\text{Volume of Water}}\\ &=\frac{0.004}{1.5}\\ &=\underline{0.003}\end{aligned}
\text{Units}=\underline{\text{mol/dm}^3}
Question 5: In an acid base reaction, 2.5\text{ dm}^3 of a 0.5\text{ mol/dm}^3 sample of phosphoric acid \left(\text{H}_3\text{PO}_4, \text{M}_r =98\right) was used to neutralize a sample of sodium hydroxide. Calculate the mass of phosphoric acid in the solution.
[3 marks]
Calculation should be broken down into steps:
Step 1: Calculation of \text{H}_3\text{PO}_4 moles.
\text{Concentratio H}_3\text{PO}_4=\frac{\text{Moles of H}_3\text{PO}_4}{\text{Volume of H}_3\text{PO}_4}
\text{Moles H}_3\text{PO}_4 = \text{Concentration H}_3\text{PO}_4 \times \text{Volume H}_3\text{PO}_4
\text{Moles H}_3\text{PO}_4 =0.5\times 2.5 =\underline{1.25\text{ mol}}
Step 2: Calculation of \text{H}_3\text{PO}_4 mass.
\text{Mass H}_3\text{PO}_4 = \text{Moles H}_3\text{PO}_4 \times \text{M}_r \text{ H}_3\text{PO}_4
\text{Mass H}_3\text{PO}_4=1.25\times98=\underline{122.5\text{ g}}
(Step 1: One mark for correct rearrangement. One mark for correct number of moles.
Step 2: One mark for correct mass)
