The Mass Spectrum and Relative Atomic Mass
The Mass Spectrum and Relative Atomic Mass Revision
The Mass Spectrum and Relative Atomic Mass
A mass spectrometer creates the mass spectrum. It can be used to find the relative atomic mass of an element.
The relative atomic mass, Ar , is the weighted average mass of an atom of an element, relative to one twelfth of the mass of an atom of carbon-12.
Calculating Relative Atomic Mass
There are two equations that can help to calculate relative atomic mass.
\text{Relative atomic mass}= \dfrac{\Sigma\left(\text{isotopic mass}\times\%\text{ abundance}\right)}{100}
\text{Relative atomic mass}= \dfrac{\Sigma\left(\text{isotopic mass}\times\text{relative abundance}\right)}{\text{total relative abundance}}
If given percentage abundance, the first equation is used, if given relative abundance the second equation is used.
Example: Calculate the relative atomic mass of this element using its % abundance values.

\begin{aligned}A_{r}&=\dfrac{\Sigma\left(\text{isotopic mass}\times\%\text{ abundance}\right)}{100}\\ &=\dfrac{\left(54\times5.8\right)+\left(56\times91.8\right)+\left(57\times2.1\right)+\left(58\times0.3\right)}{100}\\&= \dfrac{313.2+5140.8+119.7+17.4}{100}\\& = \dfrac{5591.1}{100} \\&= 55.91\end{aligned}
Using Mass Spectra to Calculate Relative Atomic Mass
You could also be asked to calculate relative atomic mass based on a mass spectrum. Mass spectra are created from data collected by the mass spectrometer. It shows the relative abundance against m/z, the mass charge ratio.
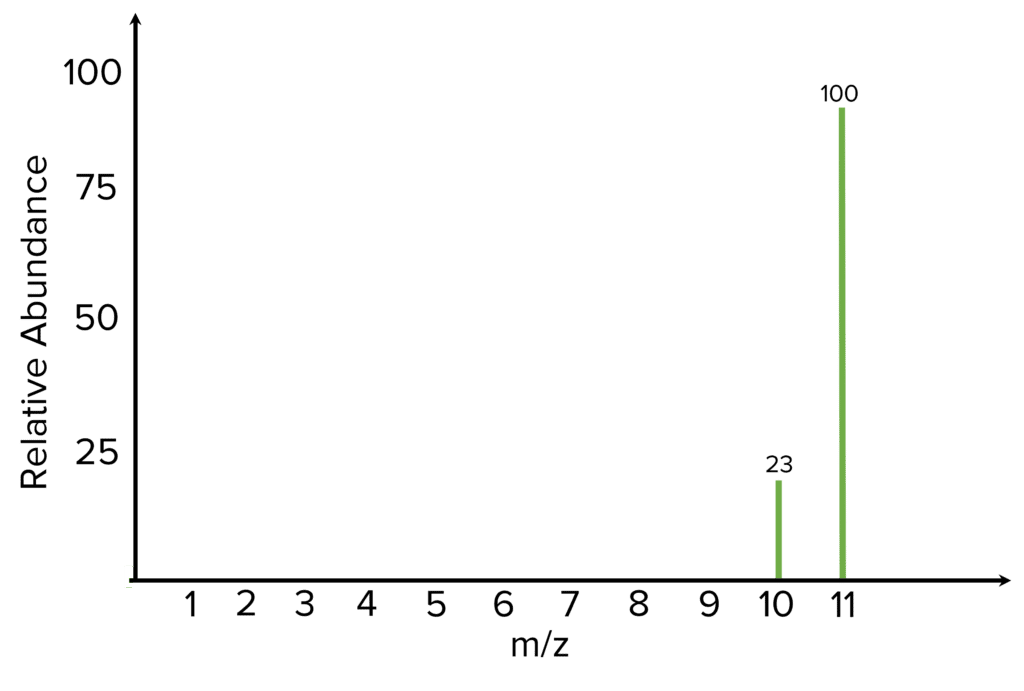

Example: Calculate the relative atomic mass of this element based on its mass spectrum.
A_{r}=\dfrac{\Sigma\left(\text{isotopic mass}\times\text{relative abundance}\right)}{\text{total relative abundance}}A_{r}=\dfrac{\left(23\times10\right)+\left(100\times11\right)}{100+23}= \dfrac{230+1100}{123}= \dfrac{2330}{123} = 10.81
Chlorine and Bromine
Chlorine and Bromine are both diatomic molecules with two isotopes.
- Chlorine: \text{Cl}^{35} \left(75\%\right) and \text{Cl}^{37} \left(25\%\right)
- Bromine: \text{Br}^{79} \left(50\%\right) and \text{Br}^{81} \left(50\%\right)
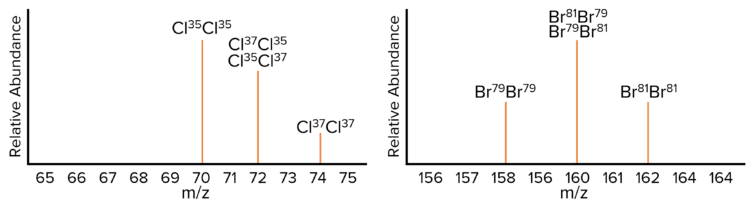
The height of the peak for bromine at \text{m/z} 160 will be due to the fact that there is double the probability of a \text{Br}^{81}\text{Br}^{79} molecule.
Fragmentation
If a molecule goes through the mass spectrometer it can be ionised by one of two processes, electron impact or electrospray ionisation.
If electron impact ionisation is used, a molecule may break up into fragments which will cause multiple peaks.
Relative molecular mass (Mr) is the average mass of a molecule of an element or a compound compared to one twelfth the mass of an atom of carbon.
To find the Mr of the molecule, you will need to find the peak with the biggest m/z value.
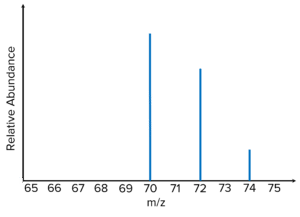
The figure below shows the mass spectra for pentane, by looking at the peak with the biggest m/z value, we can work out that the ion has an Mr of 72.
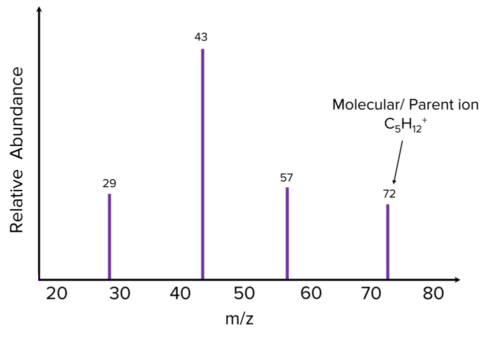
If electrospray ionisation is used, there will be no fragmentation and so there will be only one peak caused by the intact molecule. Because the molecule will have a \text{H}^+ ion added to it, to determine the Mr, 1 will need to be subtracted to account for the \text{H}^+ ion.
Example: Calculating Relative Atomic Mass Using Mass Spectra
Calculate the relative atomic mass of this element based on its mass spectrum and give the species responsible for the peak at \text{m/z }24.
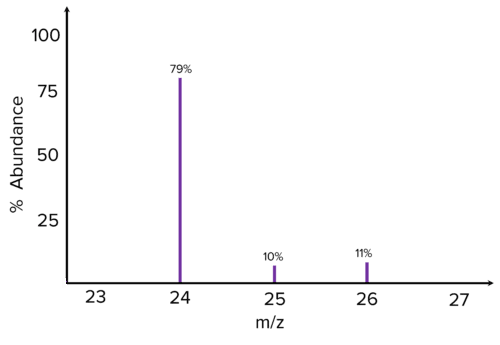
[3 marks]
\begin{aligned}A_{r}&= \dfrac{\Sigma\left(\text{isotopic mass}\times\%\text{ abundance}\right)}{100}\\&=\dfrac{\left(24\times79\right)+\left(25\times10\right)+\left(26\times11\right)}{100}\\&= \dfrac{1896+250+286}{100}\\ &= \dfrac{2432}{100} = 24.32\end{aligned}
Species responsible for peak = ^{24}\text{Mg}^+
The Mass Spectrum and Relative Atomic Mass Example Questions
Question 1: The mass spectrum shown is for chlorine \left(\text{Cl}_2\right). Identify the species that causes a peak at \text{m/z } 72.
[1 mark]
Question 2: Lithium has two isotopes of 6\text{-Li} and 7\text{-Li}. The R.A.M of lithium is 6.9. Calculate the percentage abundance of each of these isotopes.
[4 marks]
\text{Relative atomic mass} = \dfrac{\Sigma\left(\text{isotopic mass}\times\%\text{ abundance}\right)}{100}
\begin{aligned}6.90&=\frac{(6\times y)+(7\times[100-y])}{100}\\\text{}\\ 690&=6y+(7\times[100-y])\\ 690&=6y+700-7y\\690&=-y+700\\-10&=-y\\10&=y\end{aligned}
\%\text{ abundance } 6\text{-Li} = 10
\%\text{ abundance } 7\text{-Li} = 90
Question 3: Calculate the relative atomic mass for the sample and identify the element.

[3 marks]
\text{Relative atomic mass} = \dfrac{\Sigma\left(\text{isotopic mass}\times\%\text{ abundance}\right)}{100}
\text{Relative atomic mass} = \dfrac{\left(78\times0.4\right)+\left(80\times2.3\right)+\left(82\times11.6\right)+\left(83\times11.5\right)+\left(84\times57\right)+\left(85\times17.3\right)}{100}
\text{Relative atomic mass} = \dfrac{31.2+184+951.2+954.5+4788+1470.5}{100}
\text{Relative atomic mass} = \dfrac{8379.4}{100} = 83.8
The element is krypton.
You May Also Like...

MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.