Time of Flight Mass Spectrometry

Time of Flight Mass Spectrometry is a useful tool in the analysis of chemical samples. In TOF mass spectrometry, particles within a sample are ionised, the mass of the ionised particle is calculated and the element is identified.

Time of flight involves 4 different stages:

• Ionisation – This can be due to electron impact or electrospray ionisation
• Acceleration – All ions in the sample are accelerated to the same kinetic energy.
• Ion Drift/ Flight – The region of the spectrometer where the ions are separated.
• Detection – The ions are detected and recorded

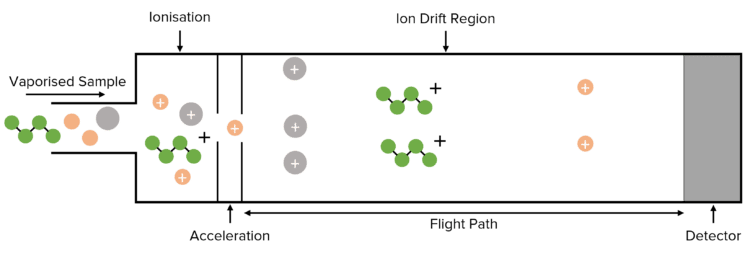
Samples are typically vaporised before being fed into the mass spectrometer. This allows for easier ionisation, and for the resulting ions to drift through the drift region.

In TOF mass spectrometry the samples are all ionised to an equal charge (usually +1). There are two ways that a sample can be ionised.

Electron Impact (Electron Ionisation)

1. An ‘electron gun’ is used to fire high-energy electrons at the sample Y.
2. The high-energy electrons remove one electron from each particle in the sample Y.
3. The loss of an electron gives the particle a +1 charge.

\text{Y}_\text{(g)} \rarr \text{Y}^+ \text{}_\text{(g)} + \text{e}^-

Electrospray Ionisation

1. Using a volatile solvent, such as ethanol, the sample Y is dissolved.
2. It is then injected through a fine, hypodermic needle which turns the sample into a mist.
3. At the tip of the needle, a very high voltage is applied, which causes the sample to become protonated (gaining an H+ ion).

\text{Y}_\text{(g)}  +  \text{H}^+ \rarr \text{ YH}^+ \text{}_\text{(g)}

Note: Electron Impact is primarily used for smaller substances with low formula masses while electrospray ionisation is used for substances with a higher mass.

Once the particles are ionised, the 1^+ ions are attracted towards the negative electric plate that generates an electric field to accelerate the ions. The electric field gives all of the particles in the sample the same kinetic energy.

The kinetic energy equation can be used to work out the kinetic energy that a particle has gained.

\text{KE} = \dfrac{1}{2}\text{mv}^2

\text{KE} = \text{Kinetic energy (J)     m} = \text{Mass (kg)     v} = \text{Velocity (ms}^{-1}\text{)}

Now that all the particles have the same kinetic energy, the velocity (the speed at which the particles travel) will depend on how heavy the particle is. Particles that are lighter, will travel faster, while those that are heavier will travel more slowly.

Note: You will need to become quite confident at rearranging equations because exam questions may not always ask you to find kinetic energy. For example, you may be asked to find distance or mass.

After moving through the electric field, the positive ions enter the flight tube. Particles will move at different velocities depending on their mass.

The velocity at which an ion moves will determine its ‘time of flight’. That is, the time it takes for the particle to move through the tube. The time of flight can be calculated by combining two equations.

Equation 1:       \text{t}=\dfrac{\text{d}}{\text{v}} 

Equation 2:      \text{KE} = \dfrac{1}{2}\text{mv}^2

Combining the Equations – Combining the equations for TOF is quite tricky. Below, is a breakdown of how to form one equation from the two to calculate TOF.

The KE equation does not include time so we have to use ‘Equation 1’ to help us find the time. We can rearrange ‘Equation 1’ to make v the subject and replace the velocity in the KE equation.

\text{v} = \dfrac{\text{d}}{\text{t}}                      \text{KE} = \dfrac{1}{2}\text{m}\left(\dfrac{\text{d}}{\text{t}}\right) ^2

We can then rearrange the equation to make t the subject, allowing us to calculate an ion’s time of flight.

\text{t} = \text{d}\sqrt{\dfrac{\text{m}}{2\text{KE}}}

\text{t} = \text{time of flight (s)}        \text{d} = \text{length of flight tube (m)}        \text{v} = \text{velocity of the particle (ms}^{-1}\text{)}

At the end of the flight tube, there is a negatively charged plate. Ionised particles collide with the negatively charged plate at different times depending on their time of flight.

When the positively charged ions collide with the detector, the detector donates electrons to the positively charged sample. The donation of an electron causes a movement of other electrons within the plate. This movement of electrons causes an electric current to be generated. The current is then measured and the size of the current used to calcualte the number of ions hitting the plate and therefore, the abundance of a given species.

The data collected from the time of flight mass spectrometer is fed into a  computer to produce a mass spectrum.

Note: Time of flight mass spectrometry has to be done inside of a vacuum because if it isn’t, the air particles would become ionised instead, which would be registered on the detector.