Empirical & Molecular Formulae

To calculate the empirical formula:

1. Find the moles of each element. This can be done by dividing the mass (or percentage mass) by the atomic mass.
2. Divide each of the moles by the smallest number of moles calculated.
3. Make sure that each of the numbers are integers.

 

Example: Calculate the empirical formula for a compound that contains 5.14\text{ grams} of Carbon, 0.86\text{ grams} of Hydrogen and 6.89\text{ grams} of Oxygen.

\text{Moles of C} = \dfrac{5.14}{12}=0.428\text{           Moles of H} = \dfrac{0.86}{1}=0.86\text{          Moles of O} = \dfrac{6.89}{16}=0.431

 

0.428 is the smallest moles calculated so all the moles will be divided by it.

 

\text{C:} \dfrac{0.428}{0.428} =1\text{          H:} \dfrac{0.86}{0.428} \approx2\text{          O:} \dfrac{0.431}{0.428} \approx1

 

Empirical Formula – \text{CH}_2\text{O}

 

To calculate the molecular formula, we use the mass of the empirical formula and \text{M}_{\text{r}} to determine how many times the mass can be divided into the \text{M}_{\text{r}}.

 

Example: Deduce the molecular formula for the compound with the empirical formula \text{C}_2\text{H}_4\text{O} and has an \text{M}_{\text{r}} of 88.

\text{Mass of C}_2\text{H}_4\text{O is }44

 

\dfrac{88}{44}= 2

So the empirical formula should be multiplied by 2.

\text{C}_4\text{H}_8\text{O}_2

 

This practical is used to measure the loss or gain of mass in different reactions such as thermal decomposition.

Water of Crystallisation is the water contained within the crystals of a hydrated salt.

In this experiment, calcium sulfate crystals are heated to remove water vapour so that the water of crystallisation in the compound can be calculated.
The equation for the reaction that takes place is \text{CaSO}_4\text{.xH}_2\text{O}_{\left(\text{s}\right)}\rightarrow\text{CaSO}_{4\left(\text{s}\right)}+\text{xH}_2\text{O}_{\left(\text{g}\right)}. 

1. Weigh an empty and dry crucible along with the lid.
2. Add 2\text{ g} of hydrated calcium sulfate to the crucible and weigh it again.
3. Heat the crucible strongly for a few minutes and then leave it to cool.
4. Weigh the crucible and its contents again.
5. Repeat steps 3-4 until the mass is constant. This would mean that the reaction is complete.

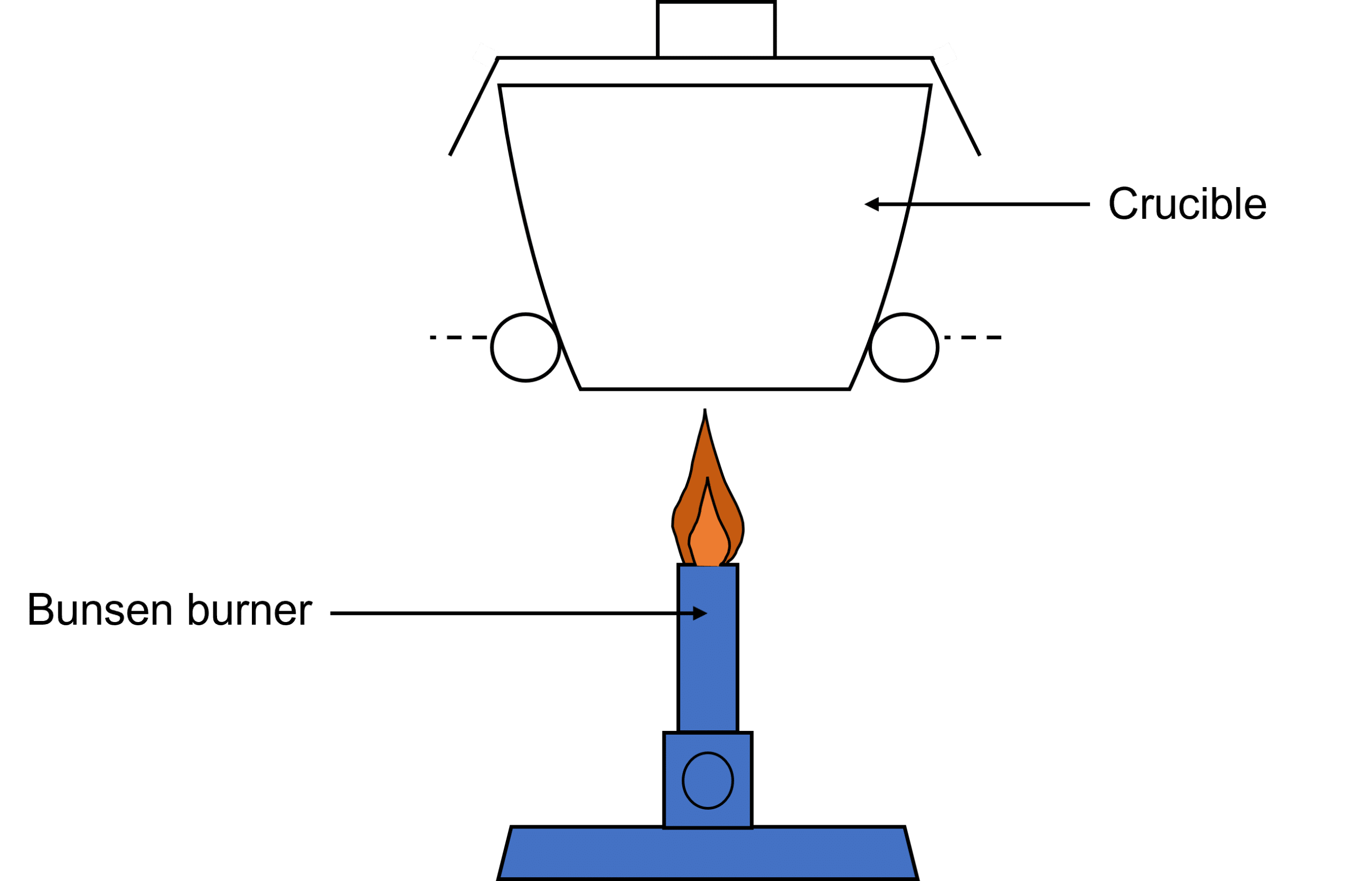
Note: When carrying out experiments in a crucible, you should not use small or large amounts of solid. If using small amounts, the weights taken will not be as accurate because of the high percentage uncertainty. For bigger amounts, there will likely be incomplete decomposition.

The water of crystallisation is the water that becomes trapped in crystalline solids when they form in solution. This water will increase the mass of the compound in which it is trapped. 

We indicate the water of crystallisation of a compound in it’s molecular formula using by writing the formula of water at the end of the compound’s formula:

\text{Na}_2\text{SO}_4\text{.H}_2\text{O}

A dot is written between the regular chemical formula and the water of crystallisation.

By heating a hydrated compound, you can work out the water of crystallisation within the compound.

Example: \textcolor{#00bfa8}{6.28\text{ g}} of sodium sulfate hydrate is heated. The mass after heating is [\textcolor{#f21cc2}{4.61\text{ g}}. Calculate the value of x in \text{Na}_2\text{SO}_4\text{.xH}_2\text{O}.

\text{Mass of H}_2\text{O}=\textcolor{#00bfa8}{6.28}-\textcolor{#f21cc2}{4.61}=\textcolor{#008d65}{1.67\text{ g}}

 

\text{Moles of Na}_2\text{SO}_4= \dfrac{\textcolor{#f21cc2}{4.61}}{142.1}=\textcolor{#008d65}{0.0324\text{ mol}}

 

\text{Moles of H}_2\text{O}=\dfrac{1.67}{18}=\textcolor{#008d65}{0.0928\text{ mol}}

 

 \text{Ratio of Na}_2\text{SO}_4\text{H}_2\text{O}=\frac{0.0928}{0.324}\approx1:3

 

\text{X}=\textcolor{#008d65}{3}