The Ideal Gas Equation

A LevelAS LevelAQA

The Ideal Gas Equation Revision

The Ideal Gas Equation

The ideal gas equation is an equation that can be used for gases and mixtures of gases. It relates the the amounts (moles and volume) of a gas to it’s physical conditions (pressure and temperature) through a physical constant (the ideal gas constant, R).

The Ideal Gas Equation

The ideal gas equation is an important formula that represents the relationship between a gases pressure, volume ,number of moles, temperature and the molar gas constant $\left(8.31\text{J K}^{-1}\text{ mol}^{-1} \right)$ .

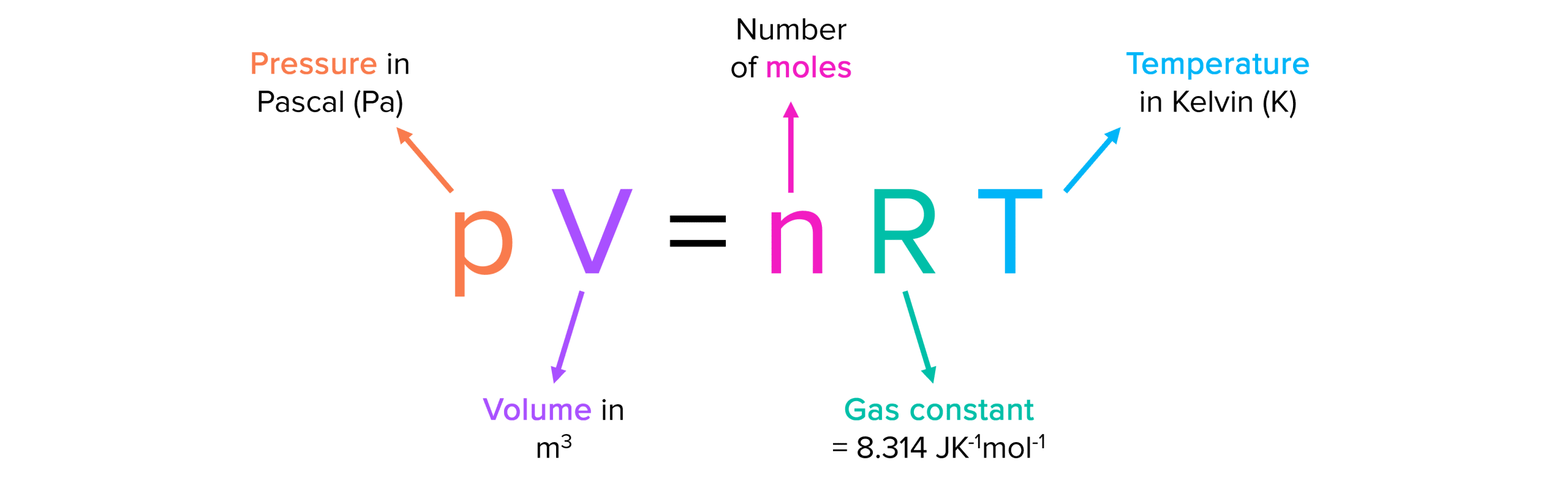
Sometimes, temperature needs to be converted from degrees Celsius $\left(\text{°C}\right)$ to kelvin $\left(\text{K}\right)$ .

To do this you must add $273$ .

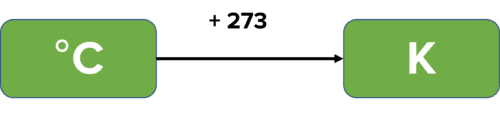
Gas Syringe

Gas syringes are usually used to measure the volume of gas produced in an experiment. The gasses produced are fed into a gas syringe by using a delivery tube. As the gas fills the syringe, it pushes back the stopper, allowing us to read off the volume of gas produced by the reaction. To prevent any loss of gas and to measure the most accurate possible volume, a bung should be placed in the top of the reaction vessel. The delivery tube is then inserted into the vessel through the bung.

Issues with Using Gas Syringes

Some gas may escape before the bung is placed on the flask.
The syringe may get stuck.
Some gases are soluble in water so it is not possible to measure the true amount of gas.

Changing Conditions

In some questions, the same amount of a gas can be put under different conditions.

An equation can be used to carry out calculations involving changing conditions:

$\dfrac{\text{p}_1\text{V}_1}{\text{T}_1}=\dfrac{\text{p}_2\text{V}_2}{\text{T}_2}$

Example: At $300\text{K}$ and $\textcolor{#00bfa8}{100\text{ kPa}}$ , $\textcolor{#f21cc2}{80 \text{ cm}^3}$ of oxygen and $\textcolor{#a233ff}{120\text{ cm}^3}$ of carbon dioxide are placed into a $\textcolor{#eb6517}{1.5\text{ dm}^3}$ evacuated flask. Calculate the pressure of the gas mixture at $300\text{K}$ in $\text{kPa}$ .

First we calculate the value of $\text{V}_1$ .

$\text{V}_1=\textcolor{#a233ff}{0.120\text{ dm}^3} + \textcolor{#f21cc2}{0.080\text{ dm}^3}=\textcolor{#008d65}{0.200\text{ dm}^3}$

Now we calculate the value of $\text{p}_2$

$\dfrac{\text{p}_1\text{V}_1}{\text{T}_1}=\dfrac{\text{p}_2\text{V}_2}{\text{T}_2}$

We can cancel out the temperature since it does not change.

$\text{p}_1\text{V}_1=\text{p}_2\text{V}_2$

Then rearrange the equation to make $\text{p}_2$ the subject and substitute in the numbers from the question.

$\begin{aligned}\text{p}_{2}&= \dfrac{\text{p}_1\text{V}_1}{\text{V}_2}\\&=\dfrac{\textcolor{#00bfa8}{100000}\times2\times10^{-4}}{1.5\times10^{-3}}\\&=13333\text{ Pa}\\&=\textcolor{#008d65}{13\text{ kPa}}\end{aligned}$

Note: The variables in the last equation have been converted to SI units before subsitution.

Reacting Volumes of Gas

$1 \text{ mol}$ of any gas at room temperature $\left(25\text{°C}\right)$ and pressure $\left(1 \text{ atm}\right)$ will have a volume of $24\text{ dm}^3$ .

In the same temperature and pressure, equal volumes of gases have an equal number of moles.

Due to this, the volume of gases reacting can be calculated by using ratios in the balanced equation.

Example: $730\text{ cm}^3$ of propane is combusted at $1\text{ atm}$ and $300\text{ K}$ . Calculate the volume of oxygen needed to react under the same conditions.

$\text{C}_3\text{H}_8 + 5\text{O}_2 \rightarrow 3\text{CO}_2 + 4\text{H}_2\text{O}$

$\text{Ratio of Propane to Oxygen}- 1:5$

$\text{Volume of oxygen}= 730\times5= 3650\text{cm}^3$

Example 1: pV=nRT

Calculate the moles of $\text{N}_2$ gas at a pressure of $\textcolor{#00bfa8}{100\text{kPa}}$ , temperature $\textcolor{#f21cc2}{30\text{ °C}}$ , volume $\textcolor{#a233ff}{450\text{ cm}^3}$ .

The molar gas constant is $8.31\text{ J K}^{-1}\text{ mol}^{-1}$

[3 marks]

$\begin{aligned}\text{pV}&=\text{nRT}\\\text{n}&=\dfrac{\text{pV}}{\text{RT}}\\&=\dfrac{\textcolor{#00bfa8}{100000}\times\textcolor{#a233ff}{0.00045}}{8.31\times\textcolor{#f21cc2}{303}}\\&=\textcolor{#008d65}{0.0178\text{ mol}}\end{aligned}$

Example 2: pV=nRT

The moles of gas in a flask of $\textcolor{#00bfa8}{12\text{dm}^3}$ is $\textcolor{#f21cc2}{0.725}$ . Use the ideal gas equation to determine the temperature $\left(\text{T}\right)$ in $\text{°C}$ , at which the pressure in the flask is $\textcolor{#a233ff}{3.3\times10^5\text{Pa}}$ .

[4 marks]

$\begin{aligned}\text{pV}&=\text{nRT}\\\text{T}&=\dfrac{\text{pV}}{\text{nR}}\\&=\dfrac{\textcolor{#a233ff}{3.3\times10^5}\times\textcolor{#00bfa8}{12\times10^{-3}}}{\textcolor{#f21cc2}{0.724}\times8.31}\\&=657\text{K}\\&=\textcolor{#008d65}{384\text{°C}}\end{aligned}$

The Ideal Gas Equation Example Questions

Question 1: A $1.48\text{g}$ sample of ethanol vapour $\left(\text{C}_2\text{H}_5\text{OH}\right)$ is at a pressure of $100\text{ kPa}$ and a temperature of $95\text{ °C}$ . Calculate the volume, in $\text{cm}^3$ , occupied by the ethanol vapour under these conditions.

[5 marks]

$\text{Number of moles}=\dfrac{1.48}{46}= 0.03217$

$\text{p}= 100000\text{ Pa and T}= 368\text{ K}$

$\begin{aligned}\text{V}&=\dfrac{\text{nRT}}{\text{p}}\\ &= \dfrac{0.03217\times8.31\times368}{100000}\\&=9.84\times10^{-4}\text{ m}^{3}\\=984\text{ cm}^3$

Save your answers with

Gold Standard Education

Question 2: In the reaction, $4\text{NH}_{3\left(\text{g}\right)}+5\text{O}_{2\left(\text{g}\right)}\rightarrow4\text{NO}_{\left(\text{g}\right)}+6\text{H}_2\text{O}_{\left(\text{g}\right)}$ , the gases formed occupy a total volume of $5.07\text{ m}^3$ at $25\text{ °C}$ and $100\text{ kPa}$ .

Calculate the amount, in moles, of $\text{NO}$ produced.

(The molar gas constant, R = $8.31\text{ J K}^{-1}\text{ mol}^{-1}$ )

[4 marks]

$\text{P}=100000\text{Pa and T}=298\text{ K}$

$\begin{aligned}\text{n}&=\dfrac{\text{pV}}{\text{RT}}\\&=\dfrac{100000\times5.07}{8.31\times298}\\&=205\text{ mol}\end{aligned}$

$\text{Moles of NO}=\dfrac{4}{10}\times 205=81.9\text{ mol}$

Save your answers with

Gold Standard Education