Concentrations and Dilutions

Concentration can be calculated using the following equation:

\text{Concentration}=\dfrac{\text{Number of moles}}{\text{Volume}}  

Concentration: \text{mol dm}^{-3} \text{or M}

Number of moles: \text{mol}

Volume: \text{dm}^3

Example: Calculate the concentration of a solution made by dissolving 0.0974\text{ moles} of \text{NaCl} in 1.5 \text{ dm}^3 of water.

\begin{aligned}\text{Concentration}&=\dfrac{\text{Number of moles}}{\text{Volume}}\\&=\dfrac{\text{0.0974}}{1.5}\\&=0.065\text{ mol dm}^{-3}\end{aligned}

 

Sometimes, you may be given a volume that is not in \text{dm}^3 and you will need to convert between the different units.

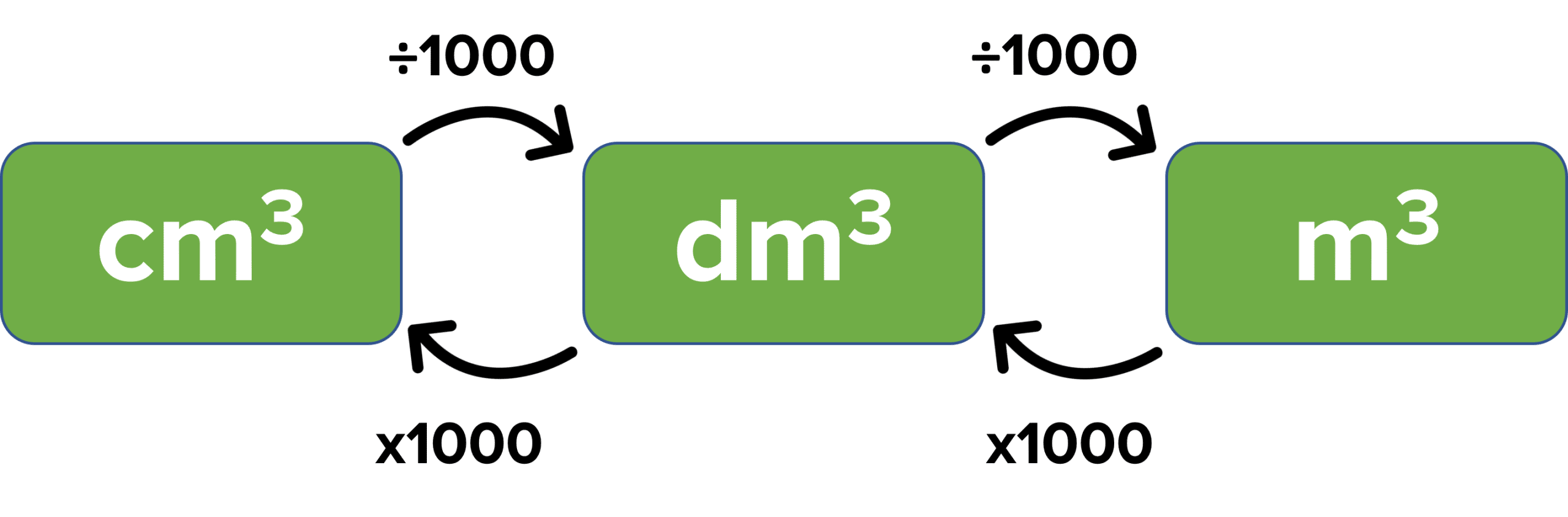
Example: A 0.826\text{ mol dm}^{-3}solution was formed by dissolving \text{CaO} in 430\text{ cm}^3 of water. Calculate the number of moles of\text{CaO} dissolved in water.

\begin{aligned}\text{Volume in dm}^3 &= 430\div 1000 =0.430\text{ dm}^3\\\text{Concentration} &= \dfrac{\text{Number of moles}}{\text{Volume}}\\\text{Number of moles}&= \text{Concentration}\times\text{Volume}\\\text{Number of moles}&=0.823\times0.430\\ &=0.360\text{ mol}\end{aligned}

 

Concentrations of solutions can also be measured using mass rather than moles so the units are \text{g dm}^{-3} instead of \text{mol dm}^{-3}.

Equation 1:

\text{Mass concentration}=\dfrac{\text{Mass}}{\text{Volume}}

 

To convert \text{mol dm}^{-3} to \text{g dm}^{-3} we can multiply the concentration in \text{mol dm}^{-3} by the \text{M}_{\text{r}} of the substance.

Equation 2: 

\text{Concentration }\left(\text{g dm}^{-3}\right)=\text{Concentration }\left(\text{ mol dm}^{-3}\right)\times\text{M}_{\text{r}}

Making a Solution

1. Weigh the container containing the required mass of solid on a balance that measures up to at least 2 decimal places.
2. Pour the required mass into a beaker and reweigh the container used. Then calculate the difference between the two recorded weights.
3. Add 100\text{cm}^3 of distilled water to the beaker and use a glass rod to stir the solution. If the solute does not dissolve, the beaker may need to be heated gently so all the solute can dissolve.
4. Using a funnel, pour the solution into a 250 \text{cm}^3 volumetric flask.
5. Rinse the beaker, glass rod and funnel and add any rinsed material to the flask.
6. With distilled water, fill the flask up to the mark.
7. Then invert the flask multiple times to allow the solution to mix well.

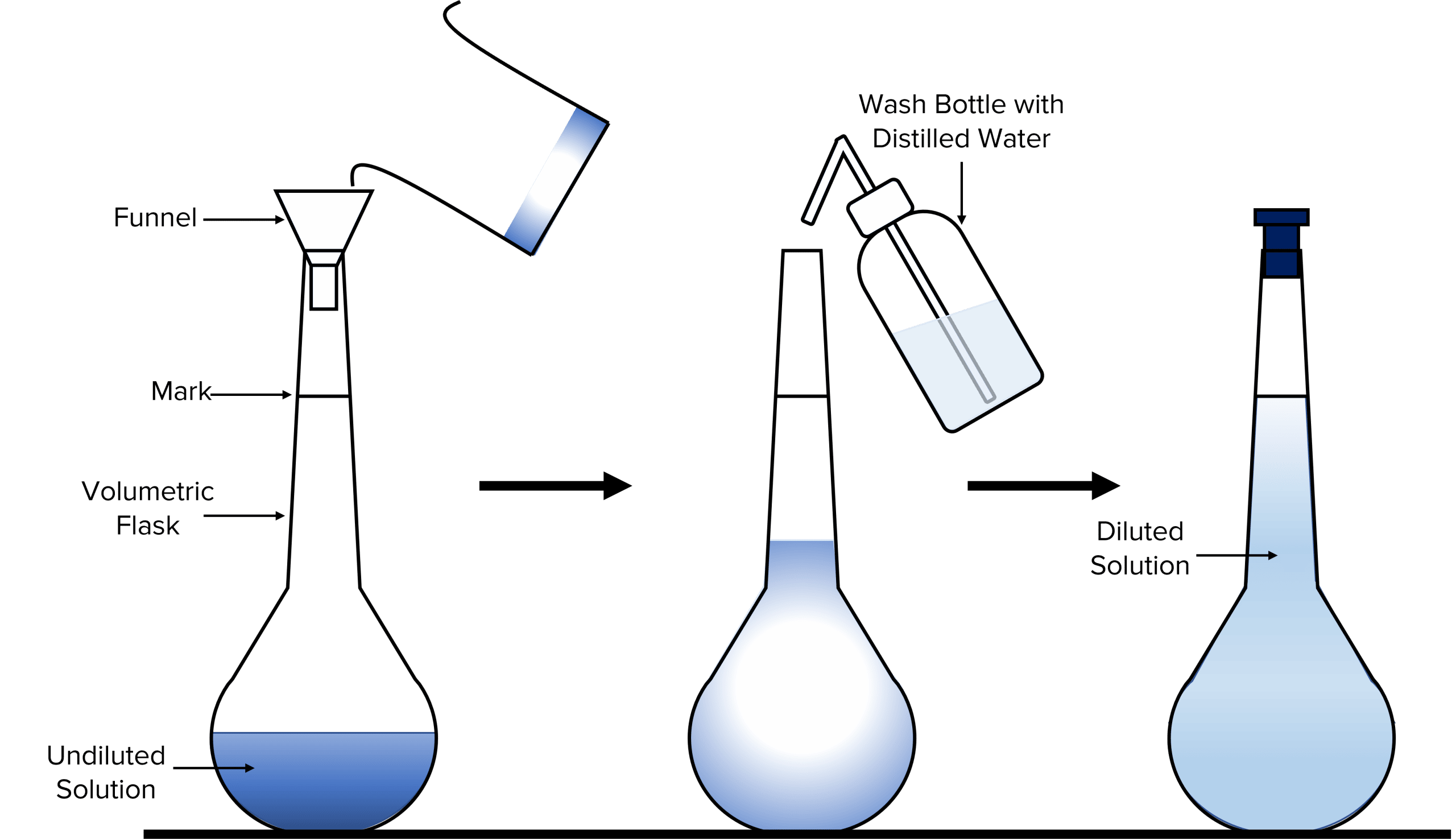
Making a Dilution

1. Using a volumetric pipette, measure out 25.0\text{ cm}^3 of the original solution into a volumetric flask of 250\text{ cm}^3.
2. Fill the rest of the flask (up to the mark) with distilled water. Use a dropping pipette for the last few drops.
3. Turn the flask upside down several times to allow the solution to mix well.

Note: We use volumetric pipettes instead of measuring cylinders because they have a smaller uncertainty which means they are more accurate.

Diluting solutions means increasing the volume of a solution and decreasing the concentration without altering the amount of moles.

Since the amount of moles stays the same we can use the concentration equation to create an equation for dilutions:

\text{C}_1\text{V}_1=\text{C}_2\text{V}_2

\text{C}_1= Original Concentration
\text{V}_1= Original Volume
\text{C}_2= New Concentration
\text{V}_2= New Volume

 

Example: 80\text{ cm}^3 of water is added to 250\text{ cm}^3 of a 0.90\text{ mol dm}^{-3} solution of \text{KOH} . Calculate the concentration of the diluted solution.

\text{C}_1\times\text{V}_1=\text{C}_2\times\text{V}_2

 

\begin{aligned}\text{C}_2&= \dfrac{\text{C}_1\times\text{V}_1}{\text{V}_2}\\&=\dfrac{0.90\times0.250}{0.330}\\&=0.682 \text{ mol dm}^{-3}\end{aligned}