Orbits of Satellites and Planets
Orbits of Satellites and Planets Revision
Orbits of Satellites and Planets
Previously we looked at circular motion. Any object in circular motion is held at a fixed radius by a centripetal force. For a satellite in orbit we need to consider where the centripetal force is coming from. We may also need to calculate the time period of an orbit or the speed of the moving object.
Orbits
When looking at the orbits of planets and satellites, it is the gravitational force that acts as the centripetal force keeping the planet or satellite at a fixed radius of orbit.
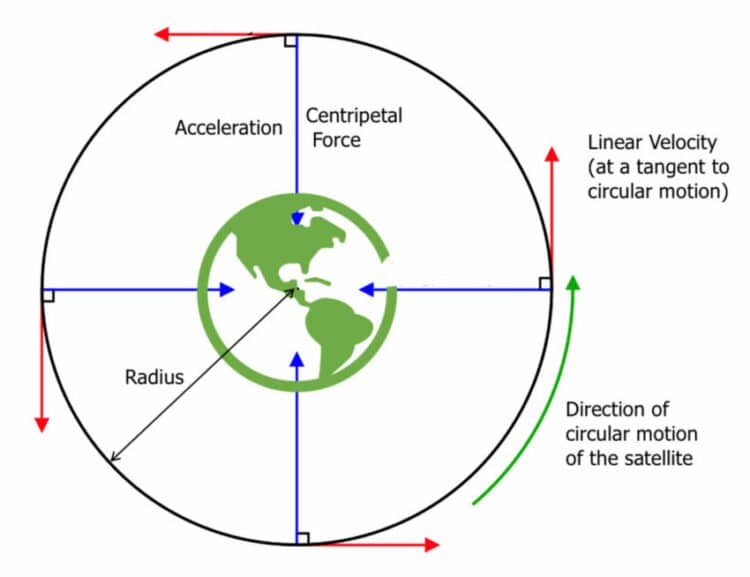
Therefore because the forces are balanced, we can say that the centripetal force is equal to the gravitational force on the satellite. From this statement we can equate the equation for gravitational force to the centripetal force.
\dfrac{GMm}{r^2} = \dfrac{mv^2}{r}
Recall that G is the gravitational constant, M is the mass of the planet, m is the mass of the satellite, v is the linear velocity of the satellite and r is the distance from the centre of the planet to the satellite.
The mass of the satellite m cancels out as it is on both sides of the equation:
\dfrac{GM}{r^2} = \dfrac{v^2}{r}
v^2 = \dfrac{GM}{r}
v = \sqrt{GM/r}
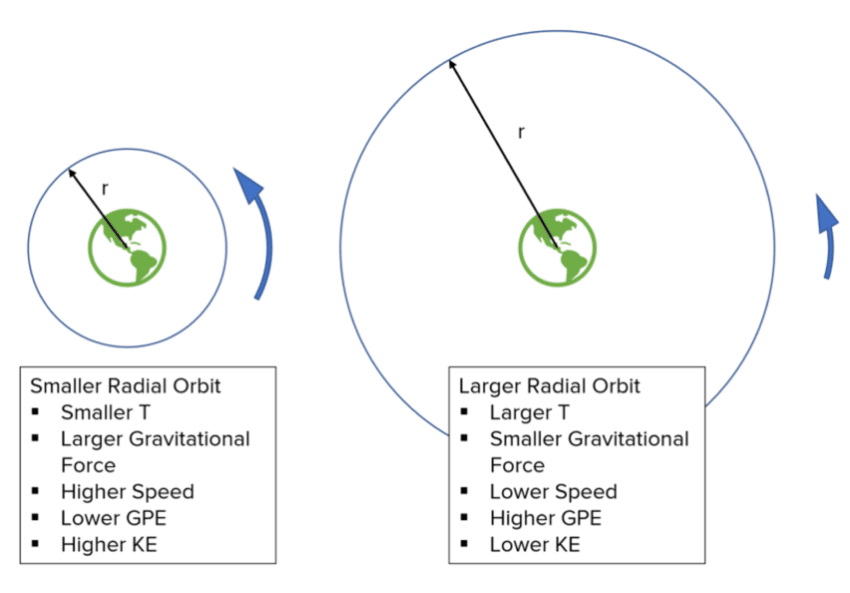
This equation can be used to calculate the exact velocity needed by a satellite to maintain a constant orbit. Less than this velocity would cause the radius of orbit to decrease, and more than this would cause the satellite to escape orbit. Also, notice that this equation is independent of the mass of the satellite.
Example: A satellite orbits the Earth at a height of 2500 \: \text{m} above the Earth’s surface. Calculate the speed of the satellite.
[3 marks]
Radius of orbit \left(r\right) = radius of Earth + height above surface
r = 6.37 \times 10^6 + 2500 = 6372500 \: \text{m}
\begin{aligned} v^2 &= \dfrac{GM}{r} \\ v^2 &= \dfrac{\left(6.67 \times 10^{-11} \times 5.97 \times 10^{24}\right)}{6372500} \\ v &= 7900 \: \text{ms}^{-1} \left(\text{to} \: 2 \: \text{s.f}\right) \end{aligned}
Time Period of Orbit
We know \: \text{velocity} = \dfrac{\text{distance}}{\text{time}}. The circumference of a satellite in circular motion is equal to 2 \pi r where r is the radius of orbit. So we can say that the velocity of a satellite in circular orbit is:
v = \dfrac{2 \pi r}{T}
where T is the time it takes the satellite to orbit once (the period). We can substitute this into our previous equation for the velocity needed by a satellite to maintain a constant orbit:
\left(\dfrac{2 \pi r}{T}\right)^2 = \dfrac{GM}{r}
This rearranged becomes:
T^2 = \dfrac{4 \pi^2 r^3}{GM}
Kepler’s third law can be derived from this equation which states that the square of the time period of a planet in circular motion is proportional to the cube of the radius:
T^2 \propto r^3
Example: Calculate the time period of the satellite that orbits the Earth at a height of 2500 \: \text{m} above the Earth’s surface.
[3 marks]
r = 6.37 \times 10^6 + 2500 = 6372500 \: \text{m}
T^2 = \dfrac{4 \pi^2 r^3}{GM}
T = \sqrt{\dfrac{4 \pi ^2 \times 6372500^3}{6.67 \times 10^{-11} \times 5.97 \times 10^{24}}}
T = 5070 \: \text{s} \left(\text{3 s.f}\right)
Energy of an Orbiting Satellite
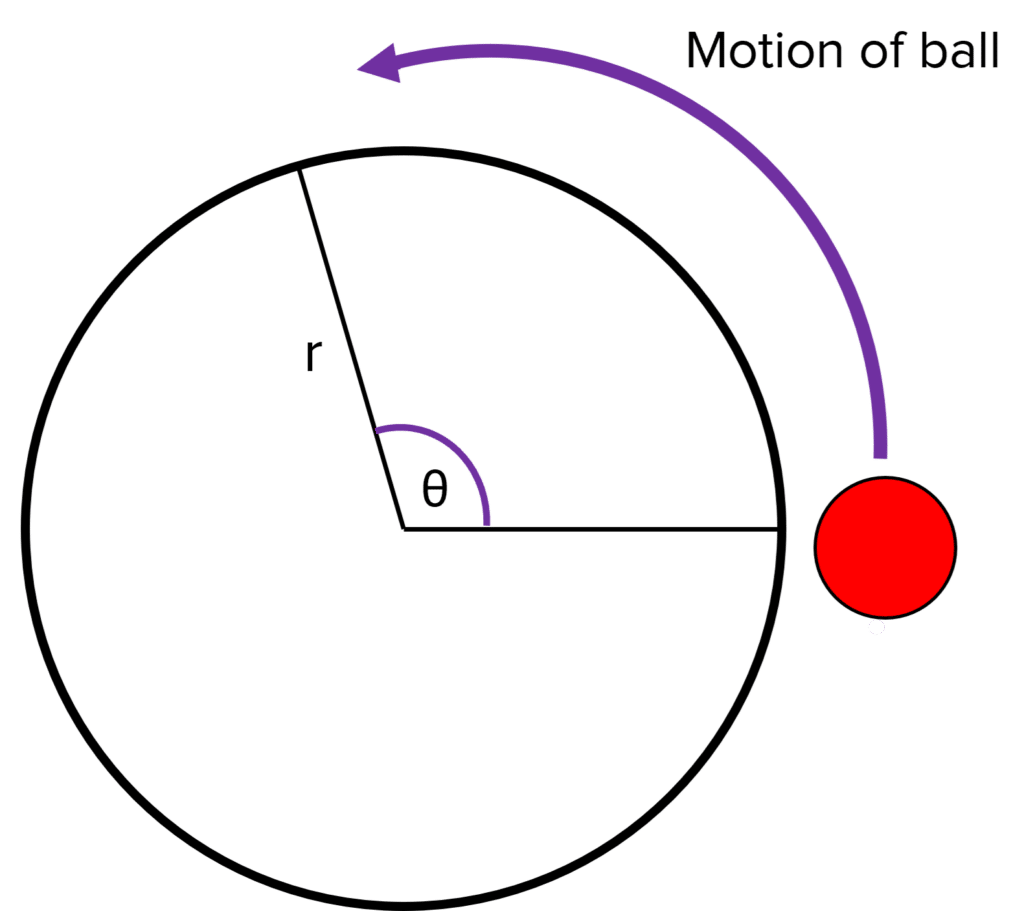

A satellite moving in circular motion possesses kinetic energy and gravitational potential energy. Combined, these give the satellite the total amount of energy needed to stay in orbit.
Imagine a ball moving in circular motion around your head on a piece of string with radius r and about an angle \theta.
If you adjust the length of the string (the radius), the speed of the ball changes. The shorter the string (the radius), the faster the ball appears to spin. This is also true for a satellite in orbit, except the string is replaced by gravitational force keeping the satellite in orbit.
As the distance from the satellite to the centre of the Earth increases (or length of string), the speed of the satellite decreases. This is because as gravitational potential energy increases, the kinetic energy must decrease as the total energy must be constant. If the kinetic energy decreases, then so must the speed (as long as the mass is constant).
Escape Velocity
Escape velocity can be defined as the velocity needed by an object to escape the gravitational field that the object is within.
The escape velocity is independent of the mass of the object but dependent upon the mass of the planet and distance away from the centre of the Earth.
It is important to note that the escape velocity calculation is for objects that do not receive an energy input once leaving the surface of the planet. Therefore, a conventional rocket which has boosters, would not need to be calculated in this way. An object’s escape velocity can be calculated by equating its kinetic energy to gravitational potential energy:
\text{Kinetic Energy} = \text{Gravitational Potential Energy}
\dfrac{1}{2} m v^2 = \dfrac{GMm}{r}
Rearranging these equations and cancelling out the mass of the object \left(m\right) gives:
v = \sqrt{\dfrac{2GM}{r}}
Example: An object is leaving the Earth’s surface. Given that the radius of the Earth is 6.37 \times 10^{6} \: \text{m} and mass 5.97 \times 10^{24} \: \text{kg} and the gravitational constant \left(G\right) is 6.67 \times 10^{-11}, calculate the escape velocity needed for the object.
[2 marks]
v = \sqrt{\dfrac{2GM}{r}}
v = \sqrt{\dfrac{2 \times 6.67 \times 10^{-11} \times 5.97 \times 10^{24}}{6.37 \times 10^6}}
v = 11.2 \times 10^3 \: \text{ms}^{-1}
Types of Orbit
Different satellites have different types of orbit depending upon their purpose.
Synchronous Orbits:
If an orbit is synchronous, the orbiting object such as a satellite orbits with the same time period and in the same direction as the planet it is orbiting. To achieve this, the velocity of the satellite must be greater than the velocity of the planet and the greater the radius of the satellite, the greater the velocity would need to be.
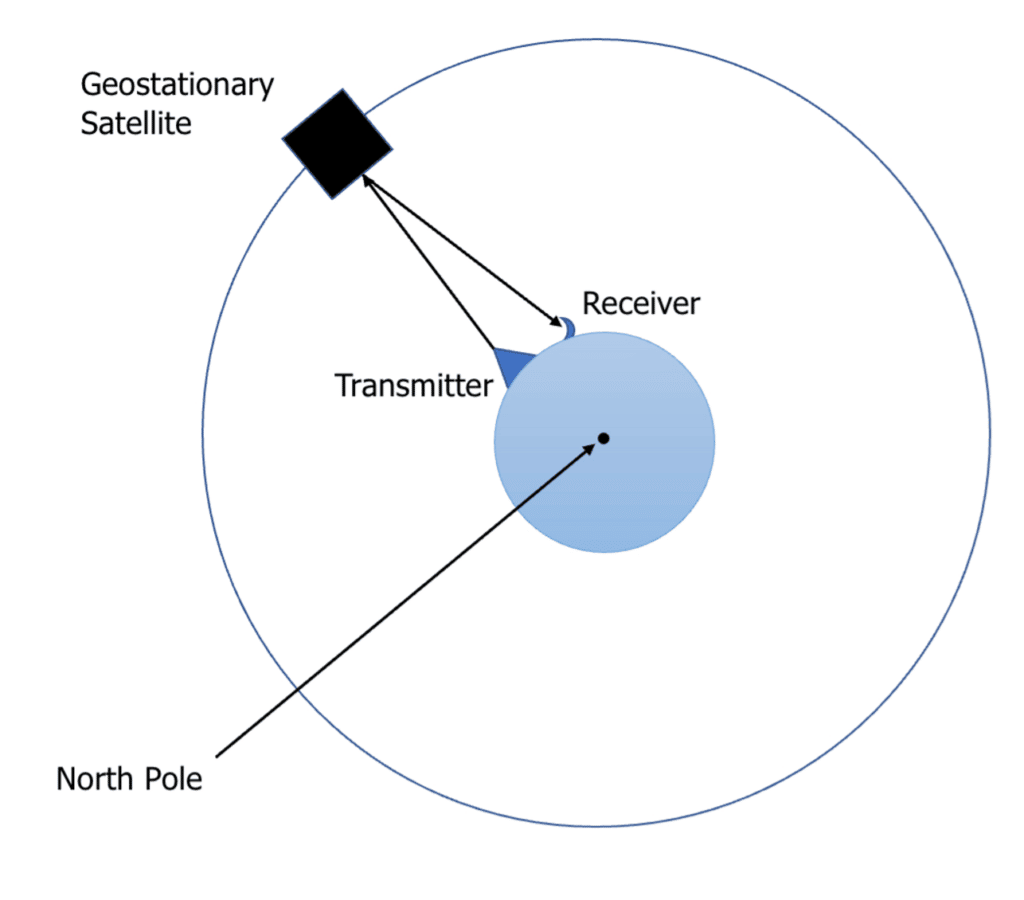

Geostationary Orbits:
A geostationary orbit is a specific type of synchronous orbit. The satellite orbits the Earth with the same time period (24 hours), above the equator and in the same plane as the equator. This causes the satellite to remain directly above the same point on the Earth at all times.
The most common purpose of a geostationary satellite is for communications. The diagram below shows a geostationary satellite used for broadcasting television.
A transmitter produces and transmits a signal to a satellite which is always in a fixed position above the transmitter. The satellite then amplifies and broadcasts the signal to the area below it. The receiver needs to be in a fixed position so that it is facing the satellite at all times to receive the signal.
Low Orbits:
A low orbiting satellite is much closer to the Earth and therefore, must be travelling at a much greater speed. As the satellite is closer to the Earth, it has the potential to get clearer and more detailed images of the Earth. This is useful for mapping the weather or taking images of the Earth.
A low orbit does not need to be geostationary. An example is a polar orbit in which the satellite orbits above the north and South Pole, perpendicular to the equator.
Orbits of Satellites and Planets Example Questions
Question 1: Calculate the velocity of a geostationary satellite orbiting 1500 \: \text{m} above the Earth.
Earth’s radius = 6.37 \times 10^6 \: \text{m}.
[3 marks]
Question 2: Explain what is meant by escape velocity.
[2 marks]
The escape velocity is the velocity needed by an object at the surface of a planet to escape the gravitational field of the planet it’s on. The object must not be propelled once leaving the surface.
Question 3: Describe the difference between geostationary and low orbits and state a use of each.
[4 marks]
A geostationary orbit requires the satellite to remain at the same point above the Earth and therefore needs to have the same time period as the Earth.
However, a low orbit can orbit in any direction and with any time period as it does not need to remain at the same point above the Earth.
Geostationary – Communications
Low orbit – Imaging or mapping the weather








