Conservation of Energy

A LevelAS LevelAQA

Conservation of Energy Revision

Conservation of Energy

Energy can take many forms around us. It gives objects the ability to do everyday things like produce heat, move, make sounds etc. This section looks at the different energy types you need to recall and the transfer of energy from one form to another.

Law of Conservation of Energy

The law of conservation of energy states “energy cannot be created nor destroyed, only transferred from one form to another”.

Therefore, in a closed system the total energy will remain the same. However, it may change from one energy form to another.

A closed system is a group of objects or devices that work together without the input of any energy or power from external sources.

Energy Types

There are several forms of energy that we need to know, describe and give examples of. These can be summarised as:

Kinetic (KE) – the energy store of an object that is moving with a specific mass at a given velocity.
Gravitational Potential (GPE) – the energy store an object has due to its mass being held at a height above the ground.
Elastic (EPE) – the energy store a stretched or compressed object has due to its elastic deformation.
Chemical – the energy stored in the bonds holding a chemical together.
Nuclear – the energy stored in the nucleus of an atom.
Internal (Thermal) – the energy stored inside an object due to its temperature.

Kinetic and Gravitational Potential Energy

Kinetic energy is the energy store an object has due to its mass and velocity. It is given by the equation:

$E_{KE} = \dfrac{1}{2} \times m \times v^2$

$E_{KE}$ is the kinetic energy in joules $\left(\text{J}\right)$
$m$ is the mass in kilograms $\left(\text{kg}\right)$
$v$ is the velocity in metres per second $\left(\text{ms}^{-1}\right)$

Gravitational Potential Energy is the energy stored by an object by its mass being held at a height above the ground. It is given by the equation:

$\Delta E_{GPE} = m \times g \times \Delta h$

$\Delta E_{GPE}$ is the change in gravitational potential energy in joules $\left(\text{J}\right)$ .
$m$ is the mass of the object in kilogram $\left(\text{kg}\right)$ .
$g$ is the gravitational field strength in Newtons per kilogram $\left(\text{N/kg}\right)$ . On earth the gravitational field strength is $9.81 \: \text{N/kg}$ .

Often objects held at a height fall to the ground. In this instance the object transfers its gravitational potential energy (GPE) store to kinetic energy (KE).

Example: A $50 \: \text{kg}$ mass falls from a height of $20 \: \text{m}$ . Describe its energy transfer and calculate the velocity of the object as it hits the ground.

[3 marks]

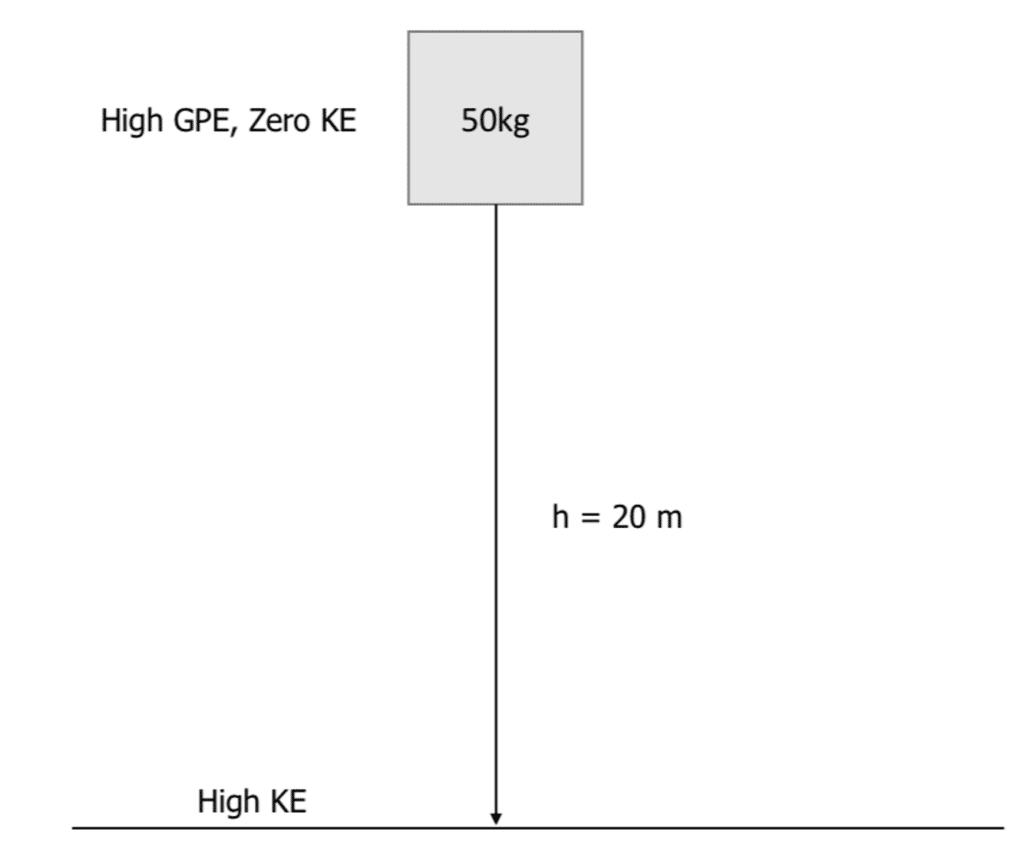
The energy transfer in this example is the object’s GPE converting to KE. In reality, small quantities of heat and sound would be produced but we are often told these are negligible and can be ignored.

As GPE converts to KE, assuming $100 \%$ efficiency, we can conclude;

$\text{GPE (at the top)} = \text{KE (at the bottom)}$ as all the GPE has transferred to KE.

Therefore:

$m \times \ g \times \Delta h = \dfrac{1}{2} \times m \times v^2$

$v^2 = \dfrac{m \times g \times \Delta h}{\dfrac{1}{2} \times m}$

$v^2 = \dfrac{2 \times m \times g \times \Delta h}{0.5 \times m}$

$v^2 = \dfrac{2 \times \textcolor{2730e9}{50} \times 9.81 \times \textcolor{cf2929}{20}}{0.5 \times \textcolor{2730e9}{50}}$

$v = \sqrt{392.4} = 19.81 \: \text{ms}^{-1}$