Work, Energy and Power
Work, Energy and Power Revision
Work, Energy and Power
One way in which energy can be transferred is when work is done. Work can be done when pushing an object, for example. Power is the rate at which this energy is transferred when work is done.
Work Done
Work done is defined as “the amount of energy transferred when a force causes an object to move”. The equation for work done is:
W = F \times s
- W is the work done in joules \left(\text{J}\right).
- F is the force in Newtons \left(\text{N}\right).
- s is the distance in metres \left(\text{m}\right).
We can see from this equation that an alternative unit for energy is \text{Nm}.
When an object is moved over a certain distance, work is done to overcome the forces of friction, air resistance and any other drag forces. For this calculation to be applied, the measurement of distance must be parallel to the direction the force is applied.
Example: If an object is moved 20 \: \text{m} with a constant force of 1500 \: \text{N}, how much work is done?
\begin{aligned} W &= F \times s \\ W &= \textcolor{bd0000}{1500} \times \textcolor{7cb447}{20} = \boldsymbol{30000} \: \textbf{J}\end{aligned}
However, often the force being applied is not parallel to the direction of motion. To calculate the work done, we need to resolve the force into its components to find the component in the direction of motion. This gives us 2 new equations:
W = F \cos \theta \times s
W = F \sin \theta \times s
Example: Calculate the work done moving the object below.
[2 marks]
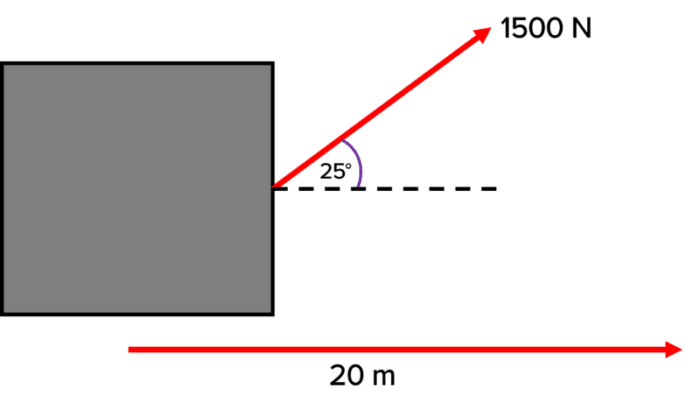
W = F \cos \theta \times s
\boldsymbol{W = 1500 \times \cos 25 \times 20 }
\boldsymbol{W = 27190} \: \textbf{J}
Power
Power and work done are related.
Power is the rate of energy transfer from one form of energy to another or from one object to another. It is also the rate of work done. Therefore it can defined using the equation:
P = \dfrac{\Delta W}{\Delta t}
- P is the power in watts \left(\text{W}\right).
- \Delta W is the work done in joules \left(\text{J}\right).
- \Delta t is the time taken for the work to be done, in seconds \left(\text{s}\right).
Example: A cyclist does 12000 \: \text{J} of work on a bicycle to move for 30 seconds. What is the cyclist’s power?
\begin{aligned} P &= \dfrac{\Delta W}{\Delta t} \\ \\ P &= \dfrac{12000}{30} = \boldsymbol{400} \: \textbf{W} \end{aligned}
Alternatively, we can use another equation to calculate power if we know the force and velocity of a moving object:
P = F \times v
- v is the velocity of the object in metres per second \left(ms^{-1}\right).
This is because:
P = \dfrac{\Delta W}{\Delta t} = \dfrac{Fs}{\Delta t} = Fv
Example: A man is moving house and carries a box, using a force of 200 \: \text{N}. He moves the box 20 metres in 10 seconds. Calculate the power.
[2 marks]
V = \dfrac{s}{t} = \dfrac{20}{10} = \boldsymbol{2} \: \textbf{ms}^{-1}
P = F \times v = 200 \times 2 = \boldsymbol{400} \: \textbf{W}
Force-Displacement Graphs
A force-displacement graph can be used to show how the force applied to an object changes over the displacement it has been moved. This is useful as forces are not always constant.
For example, a person pushing an object along the floor will need to vary their force to overcome changes in friction with the floor surface.
Work done can be calculated using a force-displacement graph by calculating the area under the graph. This is the equivalent of \text{Work} = \text{Force} \times \text{Displacement}.
Example: The graph below shows how the force of carrying an object changed with displacement. Calculate the work done carrying the object 3 metres.
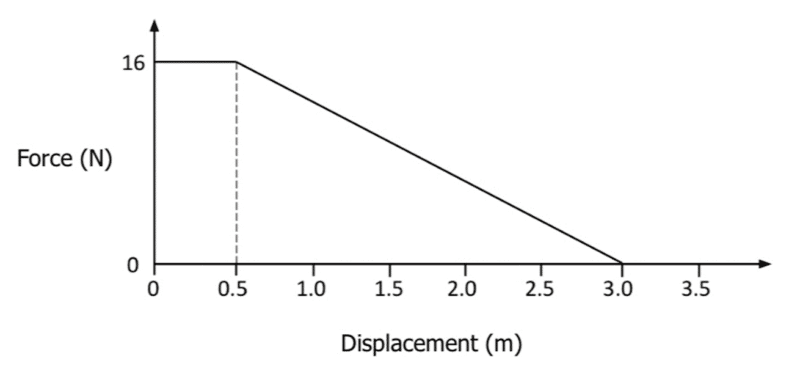
[3 marks]
Firstly, we need to split the graph into sections so that we can calculate the area of each section. This is because work done is equal to the area under a force-displacement graph.
\text{Area of rectangle} = 16 \times 0.5 = \boldsymbol{8} \: \textbf{J}
\text{Area of triangle} = \dfrac{1}{2} \times 16 \times 2.5 = \boldsymbol{20} \textbf{J}
\text{Total work done} = 8 + 20 = \boldsymbol{28} \: \textbf{J}
Efficiency
The efficiency of a system or a device is a measure of its ability to transfer the input energy into useful output energy. This can be expressed as a decimal between 0 and 1 or as a percentage from 0 to 100%. The equation for calculating efficiency as a percentage is:
\text{Efficiency} = \dfrac{\text{Useful energy output}}{\text{Total energy input}} \times 100
Or we can also use:
\text{Efficiency} = \dfrac{\text{Useful power output}}{\text{Total power input}} \times 100
No device or system can be 100 \% efficient but the more efficient a device, the less energy is wasted. If you wanted to calculate efficiency as a decimal instead of a percentage, simply don’t multiply by 100.
Example: A television requires a power input of 200 \: \text{W}. It transfers this power into 75 \: \text{W} of sound, 75 \: \text{W} of light and 50 \: \text{W} of heat. Calculate the efficiency of the TV.
[2 marks]
\text{Total input energy} = 200 \: \text{w}
\text{Total useful power output} = 75 + 75 = 150 \: \text{W}
\text{Efficiency} = \dfrac{\text{Useful power output}}{\text{Total power input}} \times 100
\text{Efficiency} = \boldsymbol{\dfrac{150}{200} \times 100 = 75 \% }
Work, Energy and Power Example Questions
Question 1: A wind turbine does 3.1 \times 10^7 \: \text{J} of work converting kinetic energy into electrical energy in one day. What is the power output of the wind turbine?
[2 marks]
Firstly, convert 1 day to seconds:
1 \times 24 \times 60 \times 60 = \boldsymbol{86400} \: \textbf{s}
\begin{aligned} P &= \dfrac{\Delta W}{\Delta t} \\ \\ P &= \dfrac{3.1 \times 10^7 \: \text{J}}{86400} = \boldsymbol{360} \: \textbf{W} \end{aligned}Question 2: A winch pulls an object with a force of 2700 \: \text{N} at 60 \degree to the horizontal. It moves 150 \: \text{m} horizontally. Calculate the work done.
[3 marks]
A diagram can be drawn to represent the information in the question:
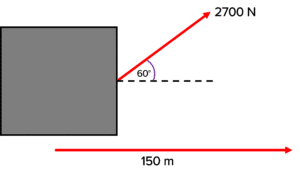
\begin{aligned} W &= F \cos \theta \times s \\ W &= 2700 \cos 60 \times 150 \\ W &= \boldsymbol{202500} \: \textbf{J} \: \text{or} \: \boldsymbol{0.2} \: \textbf{MW} \end{aligned}
Question 3: A bicycle motor produces 5 \: \text{kW} of power. The motor is 85 \% efficient at converting its power into kinetic energy. What is the maximum useful power output of the bicycle?
[3 marks]
You May Also Like...

MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.