Momentum
Momentum Revision
Momentum
Momentum is a property of all moving objects. It depends on mass and velocity. In particular we will look at Linear Momentum in this.
Linear Momentum
Momentum \left(\text{kg ms}^{-1}\right) is the quantity given by the product of mass \left(\text{kg}\right) and velocity \left(\text{ms}^{-1}\right) of a moving object.
As momentum is a vector quantity, the direction of motion usually determines if the momentum is positive or negative. Conventionally, motion to the left or downwards is considered negative, and to the right or upwards is positive.
Recall the equation for momentum:
\textcolor{aa57ff}{p = mv}
- \textcolor{aa57ff}{p} is the momentum in kilogram metres per second \left(\text{kg m/s}\right).
- \textcolor{aa57ff}{m} is the mass in kilograms \left(\text{kg}\right).
- \textcolor{aa57ff}{v} is the velocity in metres per second \left(\text{m/s}\right).
Heavy, fast moving objects, such as a lorry, have higher momentum whilst slow and light objects have lower momentum. Remember if an object is stationary then it has no momentum, because it has no velocity.
Conservation of Momentum
The law of conservation of momentum states that the total momentum before a collision is equal to the total momentum after a collision (provided no external forces act during the collision).
When two objects collide, both of their momentums need to be considered before and after the collision. In general we can write this as an equation:
\begin{aligned} \text{Momentum before} &= \text{Momentum after} \\ m_1 u_1 + m_2 u_2 &= m_1 v_1 + m_2 v_2 \end{aligned}
Example:
Two carts are moving towards each other as shown below. They collide causing the carts to move off separately in the same direction to the right. Using the information below, find the missing speed.
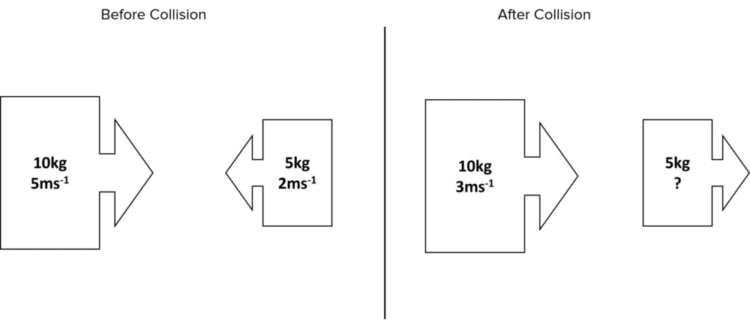
[3 marks]
\begin{aligned} \text{Momentum before} &= \text{Momentum after} \\ m_1 u_1 + m_2 u_2 &= m_1 v_1 + m_2 v_2 \\ \left(10 \times 5 \right) + \left(5 \times -2\right) &= \left(10 \times 3\right) + \left(5 \times v_2 \right) \\ 50 - 10 &= 30+ \left(5 \times v_2 \right) \\ 10 &= 5 \times v_2 \\ v_2 &= \dfrac{10}{5} = 2 \: \text{ms}^{-1} \end{aligned}Therefore, the speed is 2 \: \text{ms}^{-1} to the right.
Impulse
Impulse is a term that gives a quantity to the effect a force has on an object over a given time. It is defined in the equation:
I = F \times t
- I is the impulse in Newton-seconds \left(\text{Ns}\right).
- F is the force in Newtons \left(\text{N}\right).
- t is the time in seconds \left(\text{s}\right).
Impulse is also equal to the change in momentum during a collision. Therefore, impulse can also be written as:
I = mv - mu
mv represents the final momentum, and mu represents the initial momentum.
Because I = F \times t, we can find the impulse from a force-time graph. Here, impulse is equal to the area underneath the graph:
Example: Calculate the impulse using over the whole collision, using the force-time graph below.
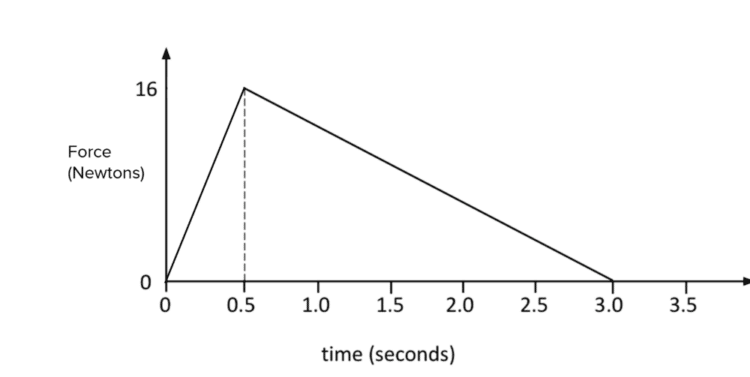
[3 marks]
\text{Impulse} = \text{Area under graph}
\text{Smaller section:} \: \boldsymbol{\left(0.5 \times 0.5 \times 16\right)}
\text{Bigger section:} \: \boldsymbol{\left(0.5 \times 2.5 \times 16\right)}
Therefore:
\text{Impulse} = 4 + 20 = \boldsymbol{24} \: \textbf{Ns}
We know that impulse is the effect a force has on an object over a given time, and it can also be defined as the change in momentum. To help understand this, let’s consider these two equations for impulse:
\begin{aligned} I &= F \times t \\ I &= mv-mu \end{aligned}Equating these:
F \times t = mv - muFor a given object, mass usually remains constant so we can rewrite this as:
F \times t = m \Delta v F = \dfrac{m \Delta v}{t}Therefore, we have used impulse to define force as the rate of change of momentum.
From this equation we can conclude that force is inversely proportional to time. So if a collision happens over a longer period of time, the force is reduced. This has many practical implications in safety and forms the basis for concepts like airbags in cars, cushioned and padded clothing etc. They all act to increase the contact time a collision occurs over. So the longer you are in contact with an air bag, the more the force on you is reduced, hence decreasing the chance of any injuries.
Collisions
Collisions can be classified as elastic or inelastic.
We have previously looked at an example of an elastic collision. This is when kinetic energy is conserved and usually occurs when the two objects remain separated after a collision.
However, an inelastic collision is where kinetic energy is not conserved and usually happens when the two objects combine as a result of the collision, forming one mass moving at one velocity.
Recall the equation for kinetic energy:
E_k = \dfrac{1}{2} \times m \times v^2
- E_k is the kinetic energy in joules \left(\text{J}\right)
- m is the mass in kilograms \left(\text{kg}\right)
- v is the velocity in metres per second \left(\text{ms}^{-1}\right)
So, for an elastic collision where kinetic energy is conserved:
\begin{aligned} \text{Kinetic Energy Before} &= \text{Kinetic Energy After} \\ \dfrac{1}{2} \times m \times v^2 &= \dfrac{1}{2} \times m \times v^2 \end{aligned}Example: Two objects collide as shown below. After the collision they move off to the right as one mass. Estimate their velocity after the collision assuming that the collision is inelastic.
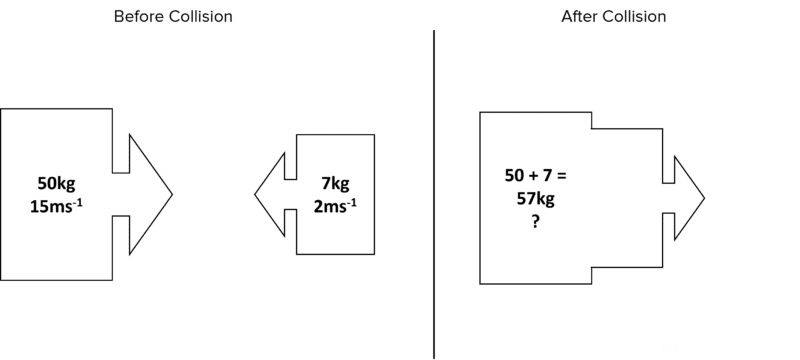
[4 marks]
- The collision is inelastic, so the kinetic energy is not conserved. However, momentum is still conserved:
\begin{aligned} m_1 u_1 + m_2 u_2 &= \left(m_1 + m_2 \right) \times v \\ \left(50 \times 15\right) + \left(7 \times -2\right) &= \left(50 + 7 \right) \times v \\ 750 - 14 &= 57 \times v \\ 736 &= 57 \times v \\ v &= \dfrac{736}{57} = 12.9 \: \text{ms}^{-1} \end{aligned}
- We can confirm ourselves that kinetic energy is not conserved in this collision and that it is inelastic:
Therefore some kinetic energy is lost in the collision and the collision inelastic.
Momentum Example Questions
Question 1: Describe the concept of the conservation of momentum and give an example of it in action.
[3 marks]
The law of conservation of momentum states that the momentum before a collision is equal to the momentum after a collision.
An example of this is when a gun is fired. When a gun is fired, a low mass bullet is fired at high speed in one direction. To conserve momentum, the gun recoils causing a small velocity of a high mass in the opposite direction.
Question 2: Explain how momentum is conserved in an explosion.
[3 marks]
When an object explodes it fires fragments off in all directions. Because momentum is a vector, some fragments would be considered to have positive momentum whilst those fired in the opposite direction, would have negative momentum. These positive and negative momentums when added together will cancel each other out and sum to zero, which is the momentum the object before the explosion. Hence, momentum is conserved.
Question 3: Describe the difference between an elastic and inelastic collision.
[2 marks]
An elastic collision is where kinetic energy is conserved, whilst an inelastic collision is where some kinetic energy is lost in the collision.
Momentum Worksheet and Example Questions
Momentum Questions
A LevelOfficial MMEYou May Also Like...

MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.