Scalars and Vectors

A LevelAS LevelAQA

Scalars and Vectors Revision

Scalars and Vectors

Quantities can be broken down into two categories, scalars and vectors. In this section we look at the difference between scalars and vectors and some examples of each. We also look at methods of resolving and combining vectors.

Difference between Scalars and Vectors

A scalar is a quantity which only has a magnitude. The magnitude is the size of the measurement.

Some examples of scalar quantities include (but are not limited to):

Temperature
Charge
Distance
Speed
Time
Energy
Volume
Density
Length

A vector quantity has a magnitude and direction. Both must be stated for vector quantities.

Some vector quantities include:

Displacement
Velocity
Force
Momentum
Acceleration

Some of the quantities above are often used incorrectly. For example, distance and displacement are often used interchangeably when they are two different quantities.

Distance is the actual distance an object has moved along the route it has travelled.
Displacement is the distance an object has travelled directly from start to finish in a straight line. This should include direction of magnitude.

Addition of Vectors

The best way to represent a vector is by using a scaled arrow. The length of the arrow represents the magnitude whilst the direction of the arrow represents the direction.

The best way to show multiple vectors is by using a diagram of all the vectors in one. The vector arrows should be placed top to tail as seen in the example below. The resultant vector is found using a straight line from the tail of the first vector, to the head of the final vector. If the two points are in the same place, then the resultant vector has zero magnitude.

Example: A jogger runs $500\: \text{m}$ east, then $200 \: \text{m}$ south. What is their displacement?

[2 marks]

As this example uses two vectors at right angles to each other, we can use calculations to work out the vector:

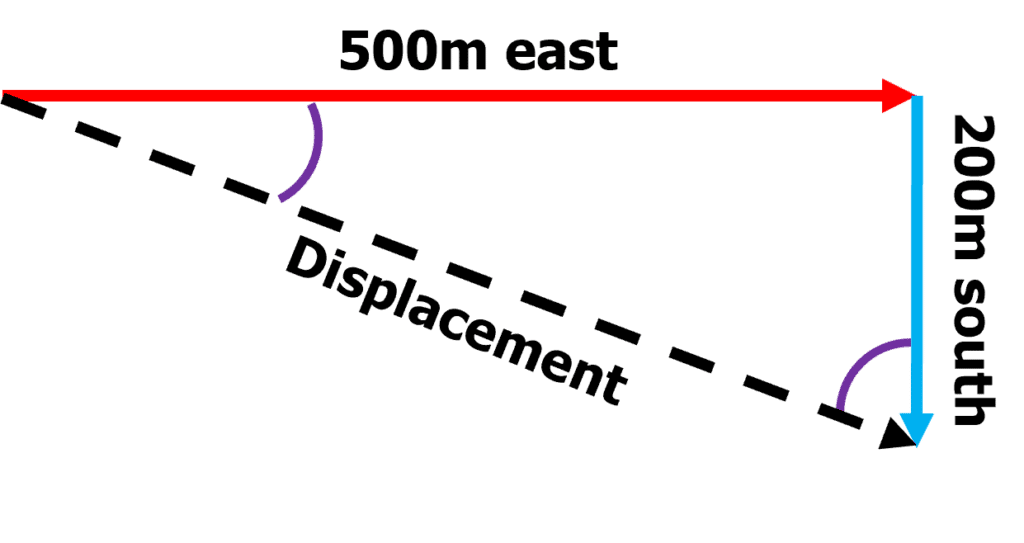
As the two vectors are acting at right angles to each other, Pythagoras’ theorem can be used to calculate the length of the arrow whilst trigonometry can be used to calculate either angle in the triangle.

$A^2 + B^2 = C^2$

$200^2 + 500^2 = C^2$

$\boldsymbol{C = 538.5 \:} \textbf{m}$

If the vectors are not acting at right angles to each other, then a scale diagram may be used. It is important to note that if this method is used, scales, lengths of arrows and measured angles need to be measured and drawn carefully. The final magnitude of the vector can be measured using a ruler and the direction measured with a protractor.

Resolving Vectors

In the opposite process from above, a vector can be resolved (separated) into two components; the horizontal and vertical components.

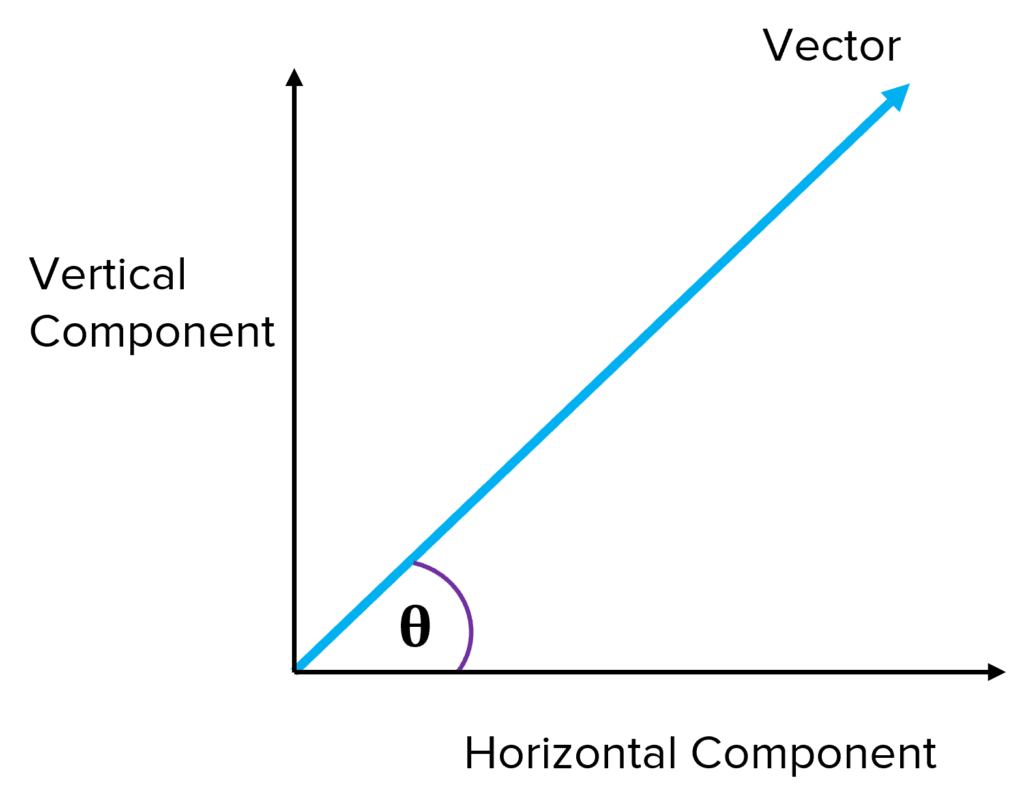
In the vector above, we could split the vector into its horizontal and vertical components. We can see that if we were to put the vertical and horizontal arrows top to tail, the blue vector is formed.

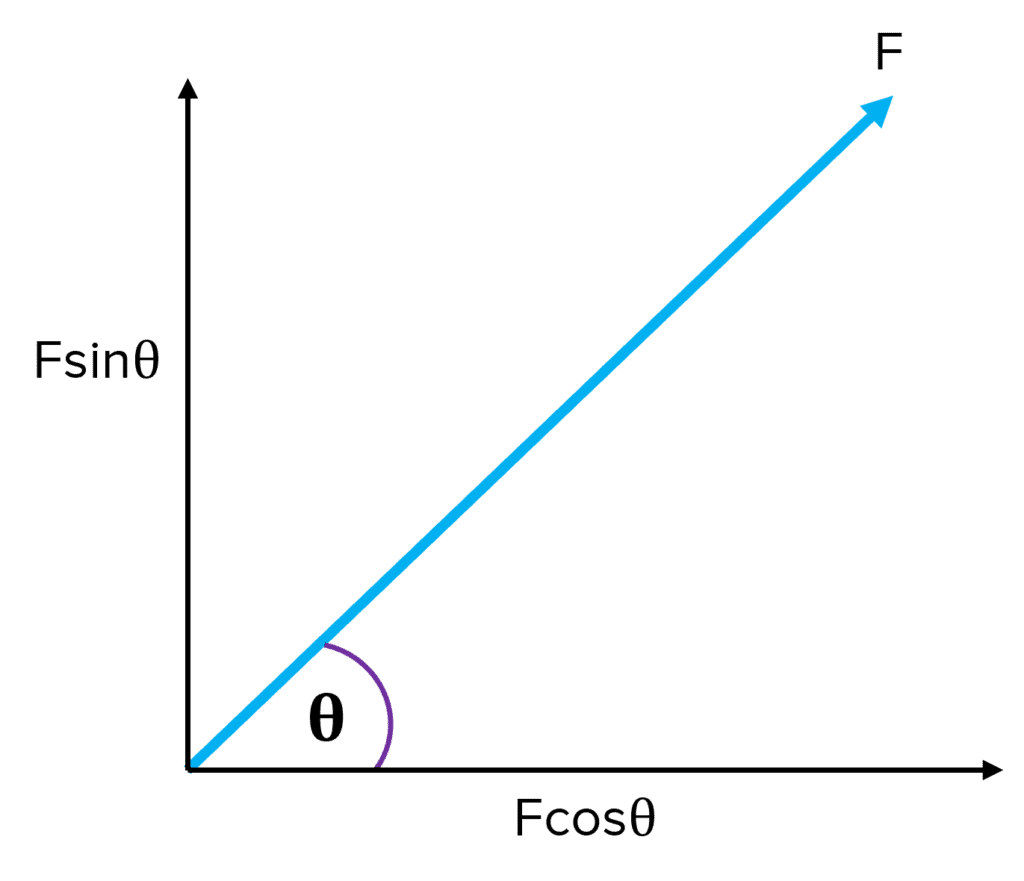
The horizontal and vertical components of this vector can be calculated using the trigonometry above, where F is the vector and theta (θ) the angle.

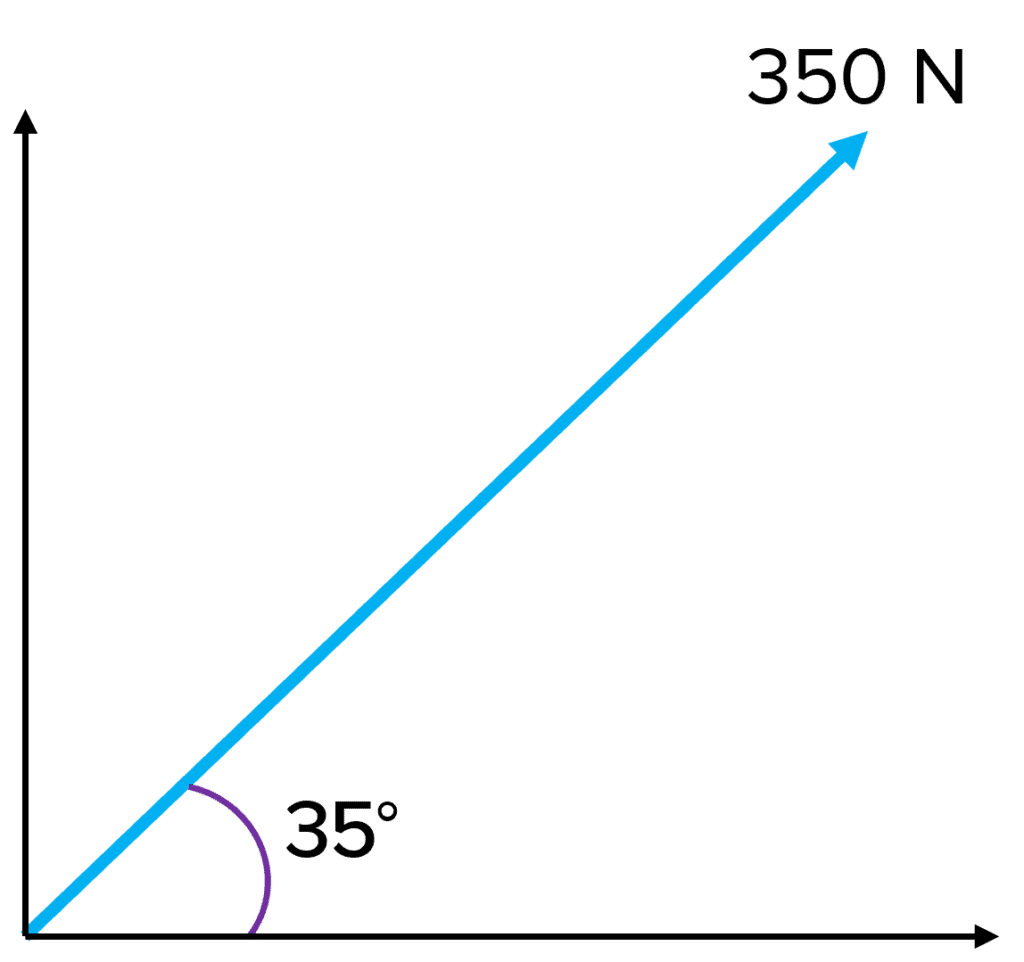
Example: Resolve the vector on the right into it’s horizontal and vertical components

[2 marks]

Using trigonometry:

$\text{Horizontal component} = 350 \times \cos\left(35\right) = \boldsymbol{290 \:} \textbf{N}$
$\text{Vertical component} = 350 \times \sin\left(35\right) = \boldsymbol{200 \:} \textbf{N}$