Refraction of Waves

A LevelAS LevelAQA

Refraction of Waves Revision

Refraction of Waves

Refraction is the process of where waves change direction as a result of moving from one medium to another. This section looks into the idea of refraction and how to calculate the refractive index of a medium.

Refraction

When light passes from one media to another it changes direction and speed. When describing the change in direction we refer to an invisible line called the normal which is at right angles to the boundary between the two media. This normal line is usually redrawn on a diagram as a dotted line.

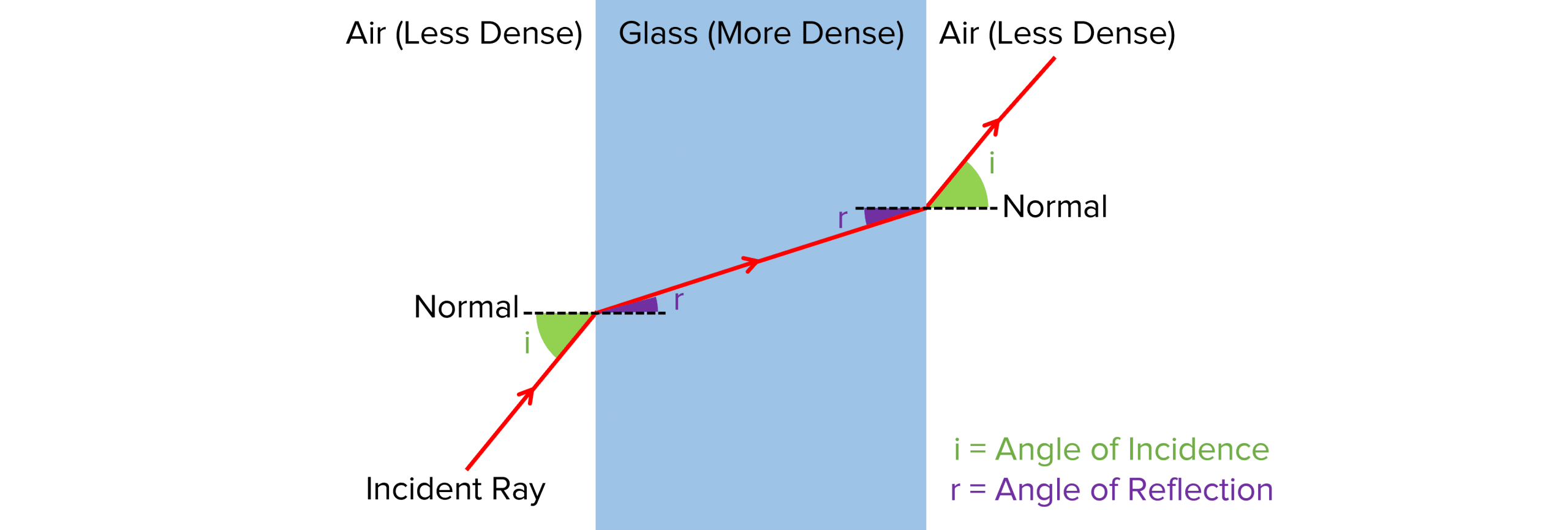
As seen in the diagram above:

When light passes from air to glass (less optically dense to more optically dense) the light bends towards the normal.
When light passes from glass to air (more optically dense to less optically dense) the light bends away from the normal.

Refraction occurs because light travels at different speeds in materials with different optical densities. In a more dense medium, the light slows down whereas in a less dense medium it speeds up. When the speed changes, the wavelength also changes but frequency remains constant. Because $v=f\lambda$ , as $v$ changes, $\lambda$ changes proportionally. This keeps $f$ constant.

The refractive index of a medium is the ratio of the speed of light in a vacuum to the speed of light in that medium. It does not have any units as it is a ratio of one speed against another. The equation for refractive index is:

$n = \dfrac{c}{c_s}$

$n=$ the refractive index (no units)
$c=$ the speed of light in a vacuum $(3\times 10^8 \text{ms} ^{-1})$
$c_s=$ the speed of light in the medium in metres per second $(\text{ms}^{-1})$

The greater the refractive index, the more the medium slows the light down and the greater the effect of refraction.

For example:

The refractive index of water is $1.333$ . Calculate the speed of light in water.

[2 marks]

$\bold{n = \dfrac{c}{c_s}}$

Rearrange for $c_s$ :

$\begin{aligned} c_s &= \dfrac{c}{n} \\ &= \dfrac{3\times 10^8}{\textcolor{00d865}{1.333}} \\ &= \bold{2.25 \times 10^8} \textbf{ms} \bold{^{-1}} \end{aligned}$

Snell’s Law

Snell’s law is an equation that allows us to calculate the refractive index of a medium or the angle at which light is refracted. The equation states:

$n_1 Sin\Theta_1 = n_2 Sin\Theta_2$

$n_1=$ the refractive index of medium $\bold{1}$
$\Theta_1=$ the angle of incidence in degrees $(\degree)$
$n_2=$ the refractive index of medium $\bold{2}$
$\Theta_2=$ the angle of refraction in degrees $(\degree)$

For example:

If the incoming ray is passing through a medium of refractive index $1.1$ into a media of refractive index $1.3$ at an angle of incidence of $45 \degree$ , what is the angle of refraction?

[3 marks]

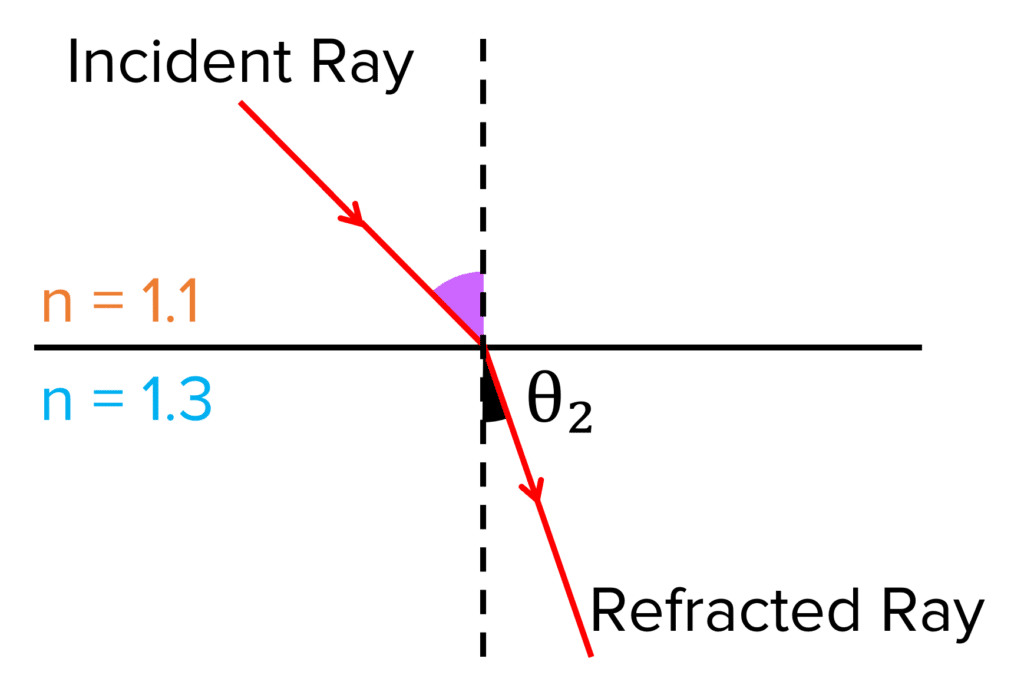
$n_1Sin\Theta_1 = n_2Sin\Theta_2$

Rearrange for $Sin\Theta_2$ :

$\begin{aligned} Sin\Theta_2 &= \dfrac{n_1}{n_2}Sin\Theta_1 \\ &= \dfrac{\textcolor{f95d27}{1.1}}{\textcolor{10a6f3}{1.3}}\times Sin(\textcolor{aa57ff}{45}) \\ &= \bold{0.598} \end{aligned} \\ \Theta_2=Sin^{-1}(0.0598) = \bold{37 \degree}$

Total Internal Reflection

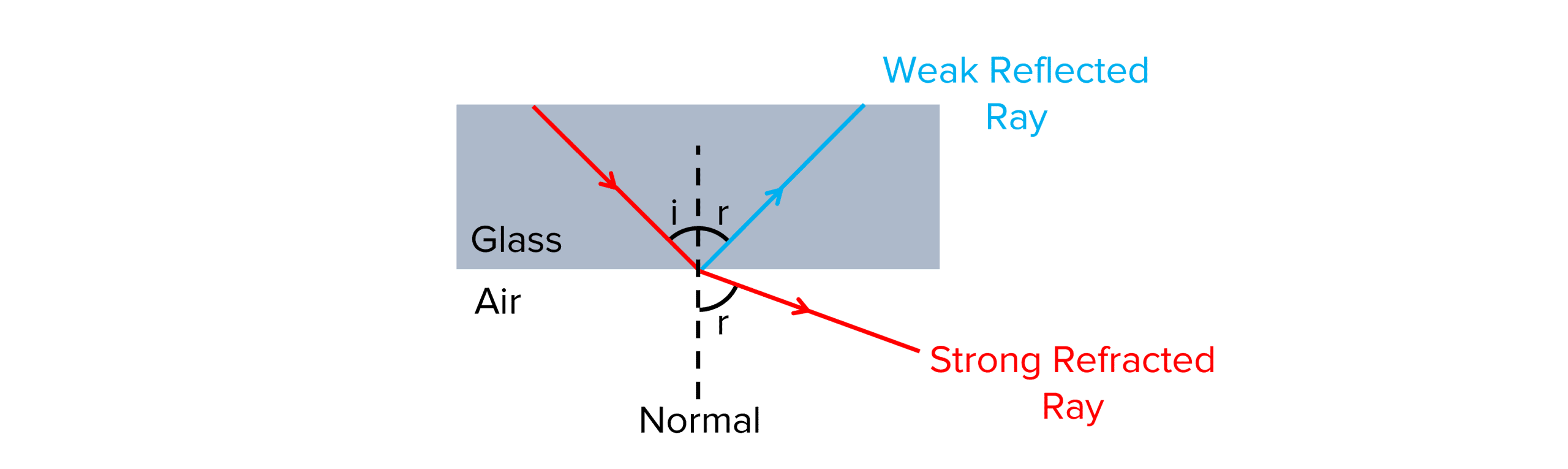
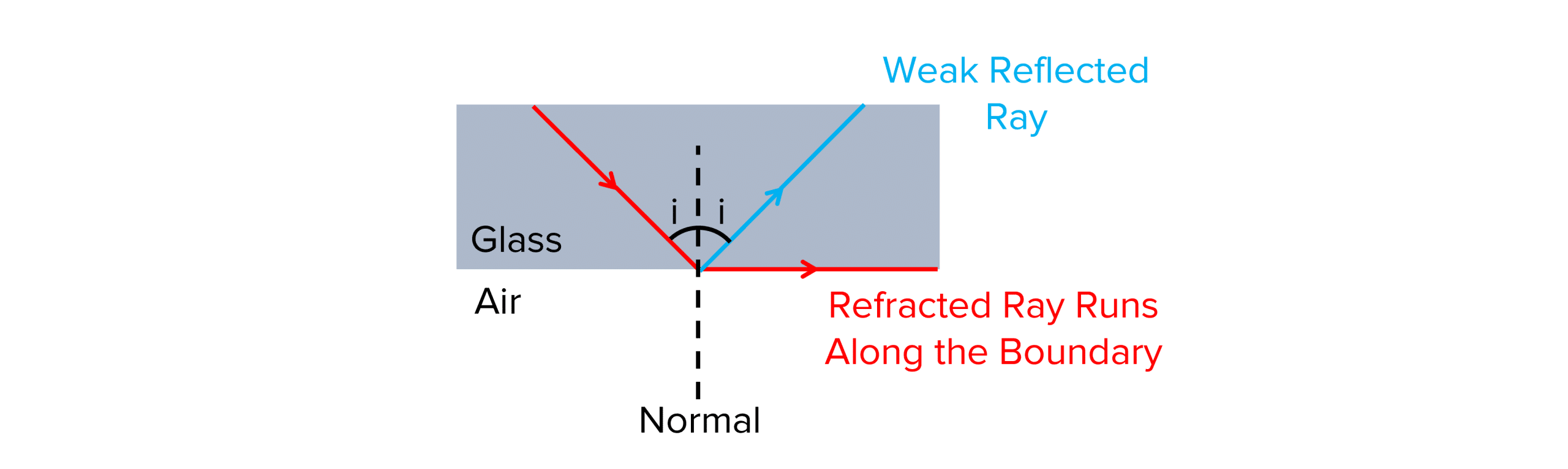
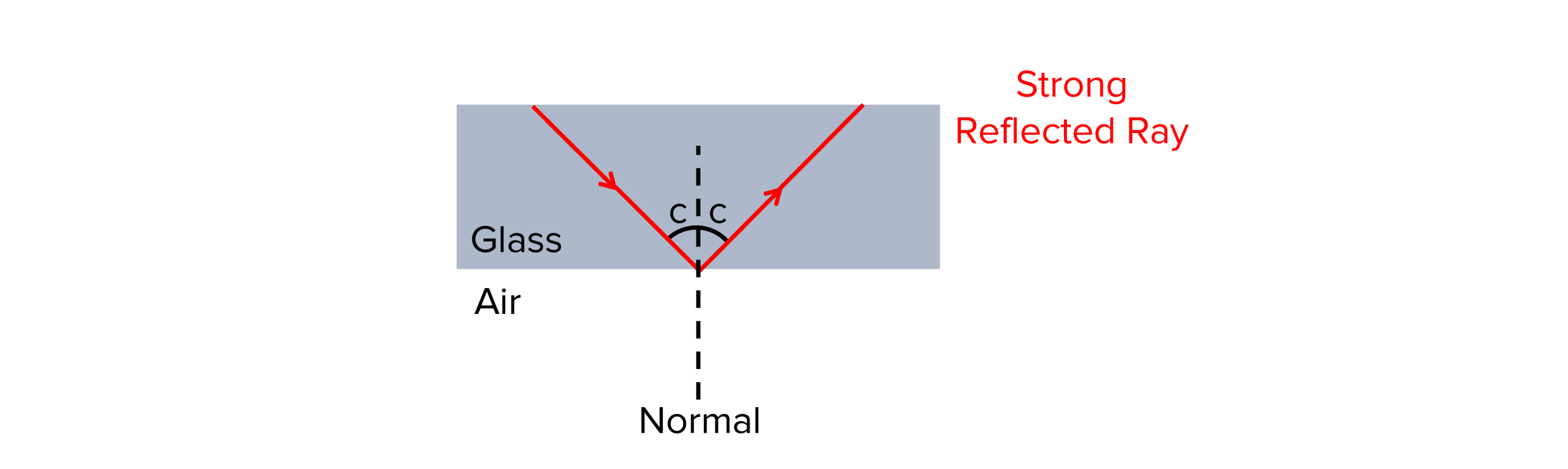
Total internal reflection occurs when all the light reflects off a boundary without allowing any light to pass through from one medium to the other.

For total internal reflection to occur, certain conditions need to be met:

The refractive index of the medium must be less than the refractive index of the next medium at the boundary.
The angle of incidence must be greater than the critical angle of the media.

The process of total internal reflection is shown below:

The idea of total internal reflection can be used in a variety of ways. The main use is in fibre optic cabling which is found inside endoscopes and internet cables.