Diffraction of Waves
Diffraction of Waves Revision
Diffraction of Waves
Whenever waves pass through an opening they diffract. Diffraction is the process of waves spreading out and the extent of the diffraction is dependent on the wavelength of the wave and the size of the opening they are passing through.
Single Slit Diffraction
When the width of the opening is appropriately the same size as the wavelength of the wave, the greatest extent of diffraction can be seen. The bigger the opening in comparison to the wavelength, the less his effect is noticed.
Diffraction can be seen in the diagram below:
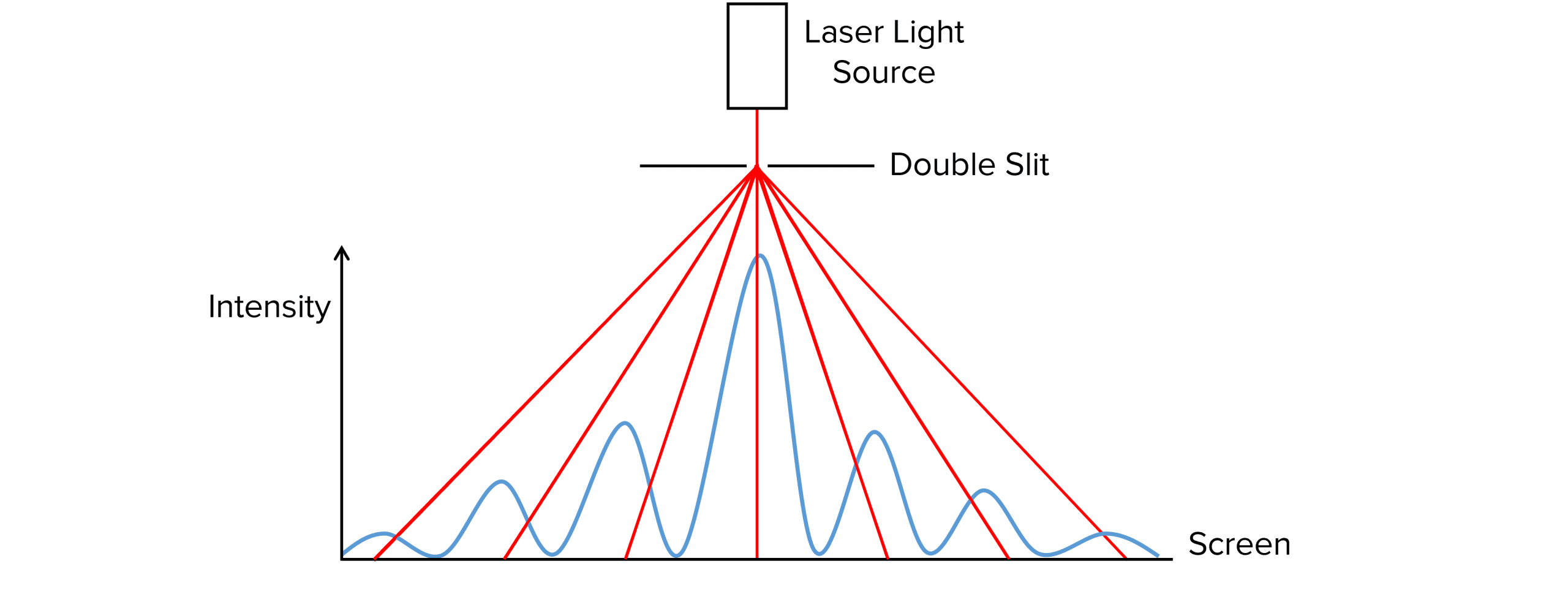
A laser can be passed through a single slit of opening similar to that of the wavelength of light from the laser. The diffracted light is projected onto a screen for analysis. A distinct diffraction pattern is seen on the screen.
If we conduct the same experiment but with light of a greater wavelength, we would see the same pattern but each fringe would be wider and the fringes further apart. This is because longer wavelengths diffract more than shorter ones.
If we kept the same blue laser with the same wavelength but narrowed the slit, the fringe spacing would be wider as more diffraction would occur and the intensity of all the fringes would decrease.
Diffraction Gratings
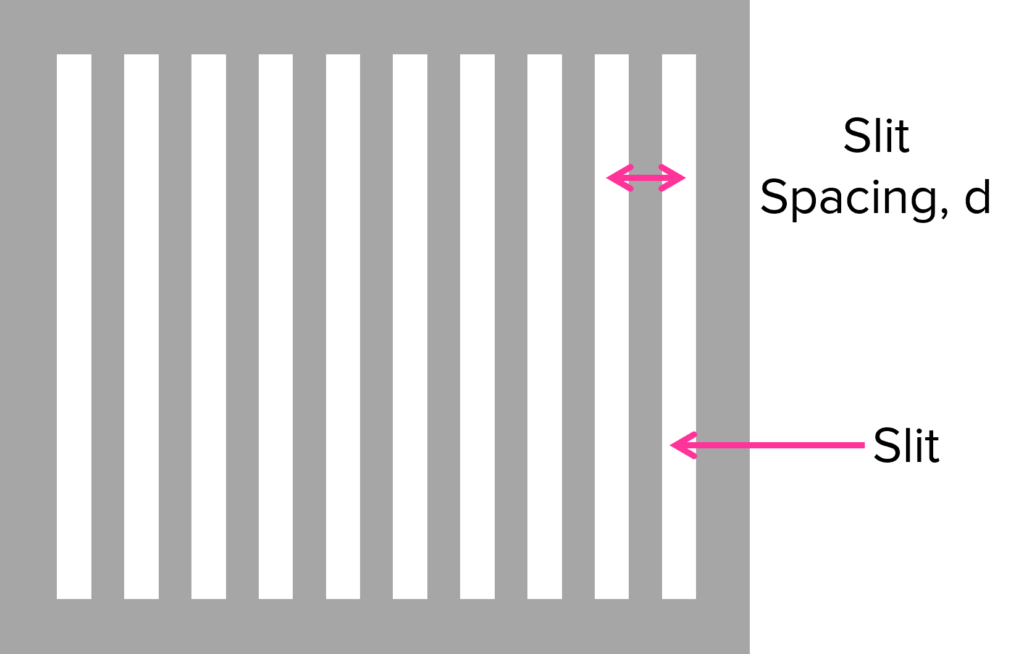

A diffraction grating is a plate with a large number of slits in it. The slits are very close together and the size of each slit is very narrow.
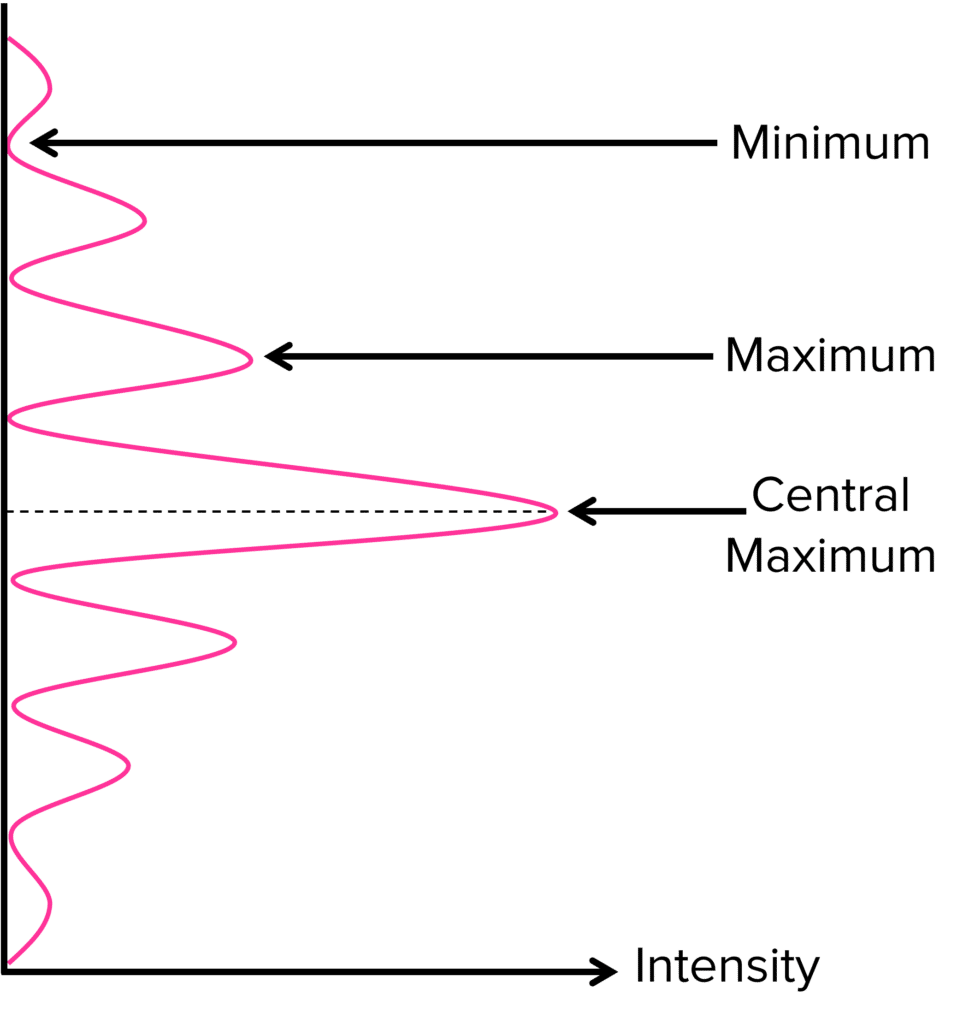

A diffraction grating also can be used to produce a diffraction pattern on a screen, as seen with the single slit. Areas of maxima (constructive interference) and minima (destructive interference) can be seen on a screen away from a central maxima.
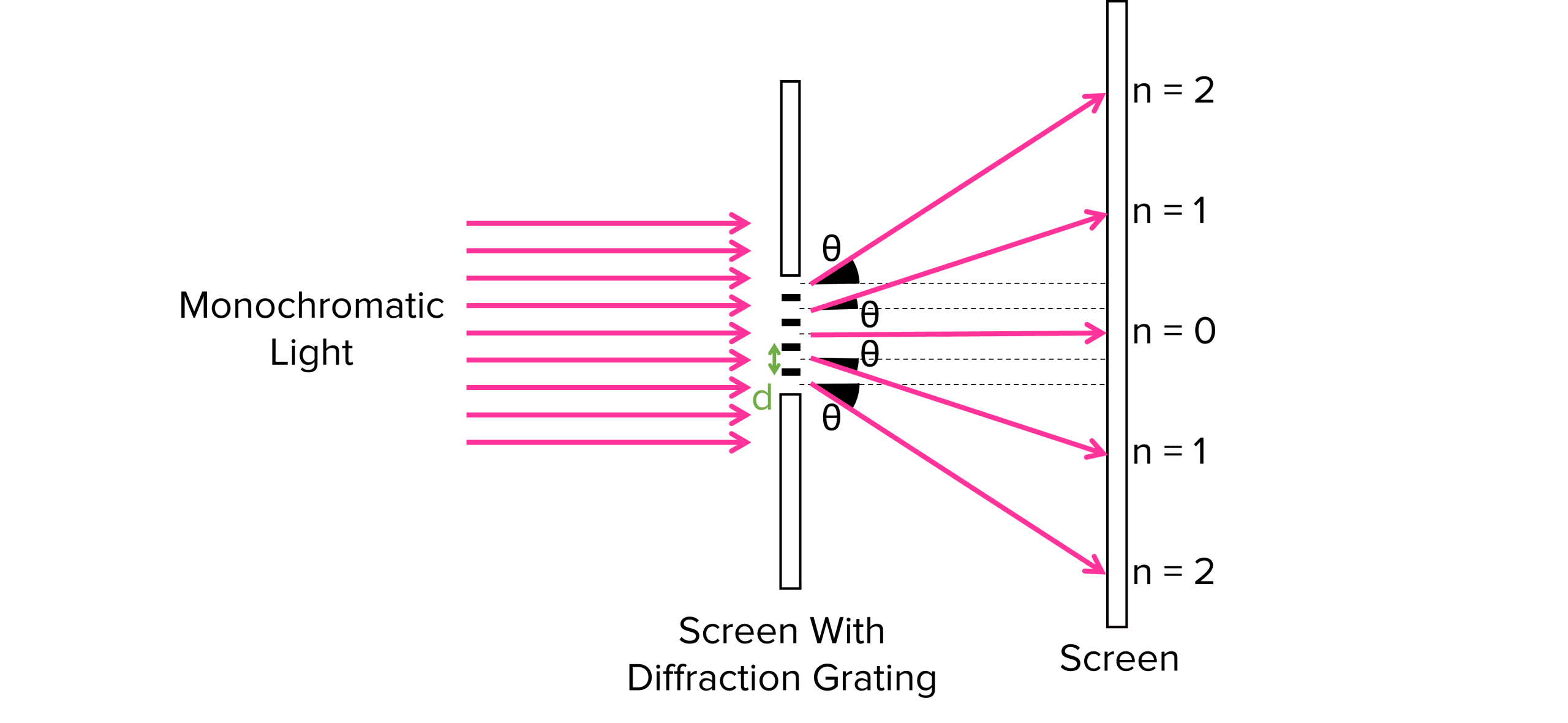
An equation can be used for diffraction gratings which gives us the angle to the normal of each maximum:
dSin\Theta = n \lambda
- d= the space between each slit in metres \text{(m)}
- \Theta= the angle between the normal and the path to the maximum in degrees (\degree) or radians \text{(rad)}
- n= the order of maxima, 0 being the central maximum, 1 being the first maximum etc
- \lambda= the wavelength of light in metres \text{(m)}.
Example:
A diffraction grating has slit separation of 1.5 \,\mu\text{m}. Monochromatic light of 400 \text{ nm} is passed through the diffraction grating to produce a diffraction pattern on a screen. Calculate the angle to the first maximum.
[2 marks]
\bold{dSin\Theta} = \bold{n\lambda}
Rearrange to find Sin\Theta:
\begin{aligned} Sin\Theta &= \dfrac{n\lambda}{d} \\ &= \dfrac{1 \times 400 \times 10^{-9}}{1.5 \times 10^{-6}} \\ &= 0.2667 \end{aligned} \\ \begin{aligned} \Theta &= Sin^{-1}(0.2667) \\ &= \bold{15.5 \degree} \end{aligned}
Diffraction gratings have many purposes:
- Produce spectrometers (devices used to separate light of different wavelengths)
- Analyse light from stars
- Analyse the composition of stars
- X-ray crystallography
Diffraction of Waves Example Questions
Question 1: What is diffraction and what conditions would cause the most diffraction to occur?
[2 marks]
Diffraction is the spreading out of a wave as it passes through a small gap. This occurs most when the wavelength of the wave and the gap are similar in size.
Question 2: Describe some of the uses of diffraction gratings.
[3 marks]
Any 3 uses from:
- Producing spectrometers (devices used to separate light of different wavelengths)
- Analysing light from stars
- Analyse the composition of stars
- X-ray crystallography.
Question 3: A diffraction grating has slit separation of 2.1 \, \mu\text{m}. Monochromatic light of 600 \text{ nm} is passed through the diffraction grating to produce a diffraction pattern on a screen. Calculate the angle to the second maximum.
[2 marks]








