Interference

Coherent waves are often used when observing interference. Two waves are coherent if they have the same frequency, same wavelength and are kept at a constant phase difference.

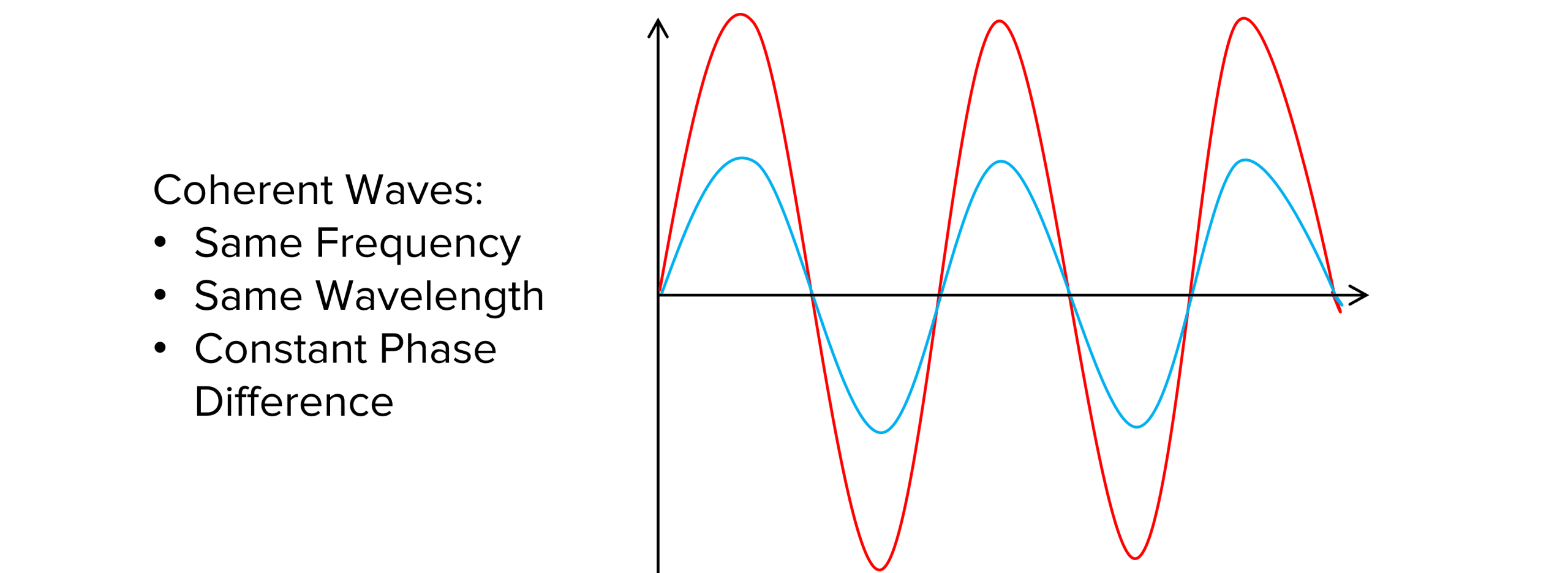
We do not often study interference using white light because it is a spectrum of colours, each with a different frequency and wavelength. It is therefore, not coherent.

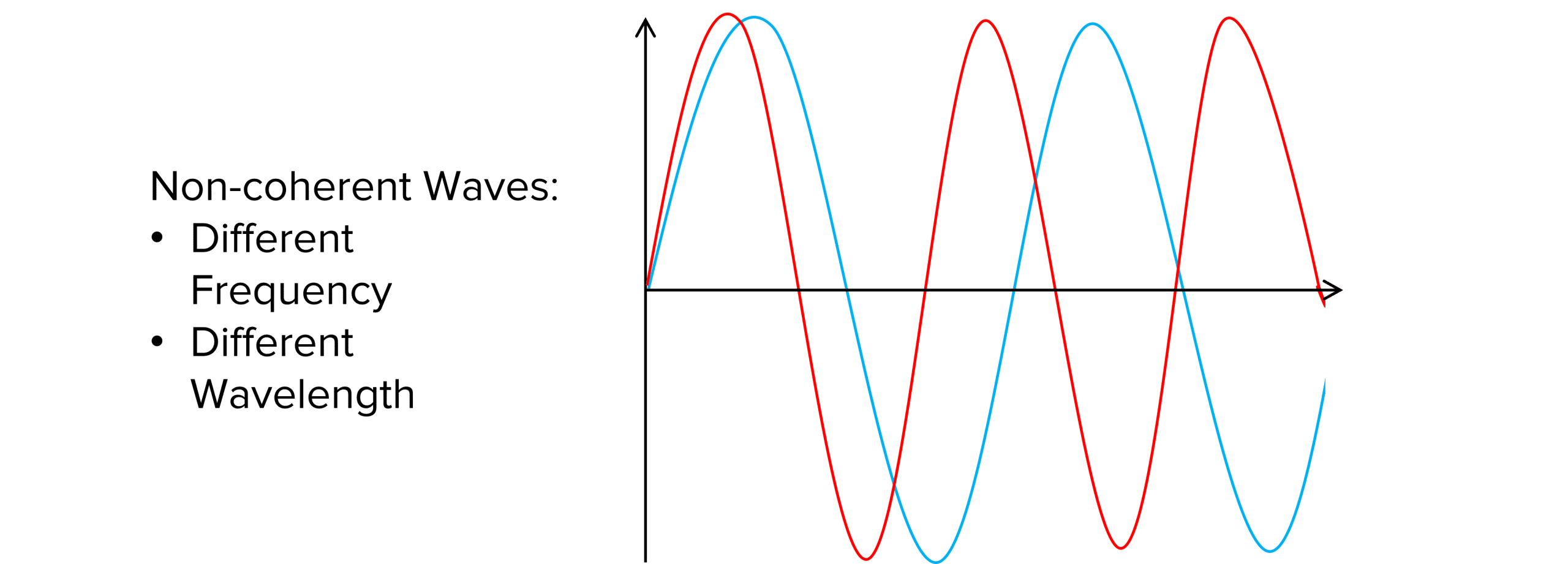
The best source of coherent light is a laser. A laser produces light of a single frequency, wavelength and at a constant phase difference. When using lasers it is important to consider the safety implications of using the laser:

• Only use the recommended power laser. Schools are only permitted to use lasers of maximum power 1\text{ mW} which minimises the risk to students.
• Ensure suitable warnings are placed around the room and outside of the room to make people aware of the danger. 
• Appropriate eye-wear should be worn and the laser should never be pointed toward someone’s face/eyes. 
• Stand behind the laser unless completely necessary to move in front. 
• Avoid shiny reflective materials that may reflect the laser as even the reflection may cause permanent damage.

The path difference of two waves can be defined as:

The difference in the distance travelled by two waves to a given point.

This is measured in metres and each distance should be measured from the source to the point where the two waves meet, usually in a screen for most experiments. However, this measurement is usually expressed in terms of the wavelength of the wave e.g 10 \lambda meaning 10 times the wavelength. 

If the path difference of two coherent waves is a whole number of wavelengths (n \lambda), constructive interference occurs. This occurs as the peaks and troughs of the waves line up and superposition occurs. 

If the path difference is a whole number and a half wavelength (n+\dfrac{1}{2})\lambda, then complete destructive interference occurs as the peaks line up with the troughs of each wave, completely cancelling each other out. 

Interference:

When two waves meet and interfere, they form a wave with the amplitude of the two waves combined. 

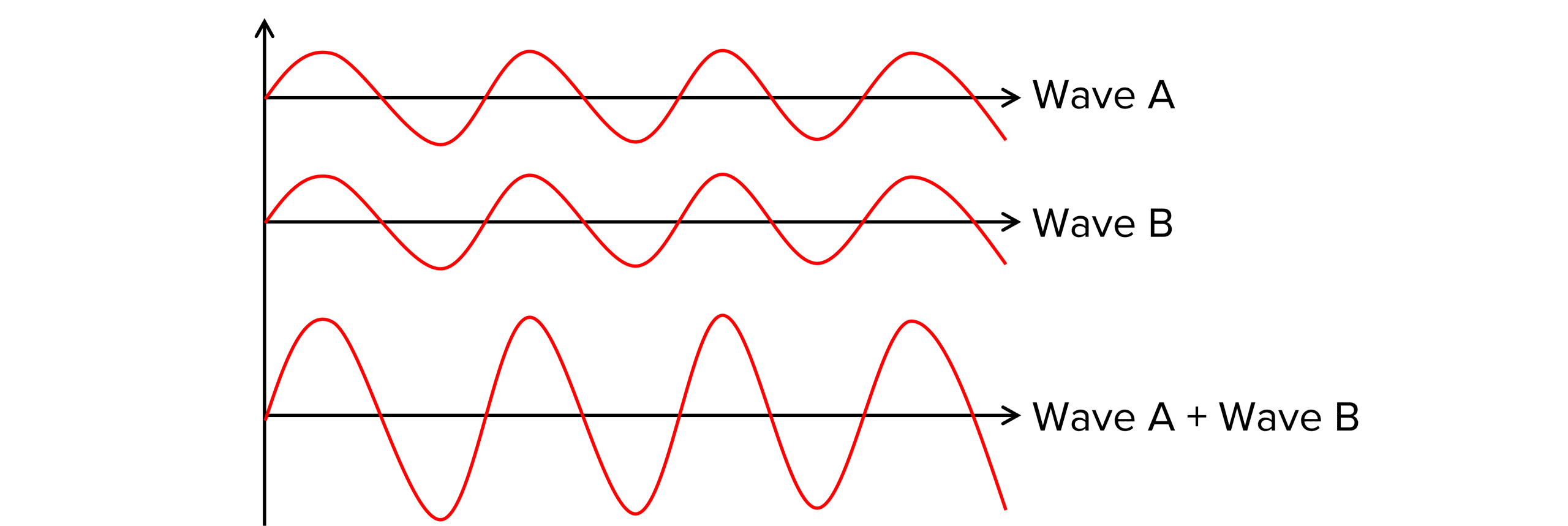
Constructive interference – The diagram above shows constructive interference. The two waves on the bottom are in-phase and therefore constructively interfere producing a wave with the amplitude of both waves combined. When the waves are completely in-phase, a new wave of maximum amplitude is formed.

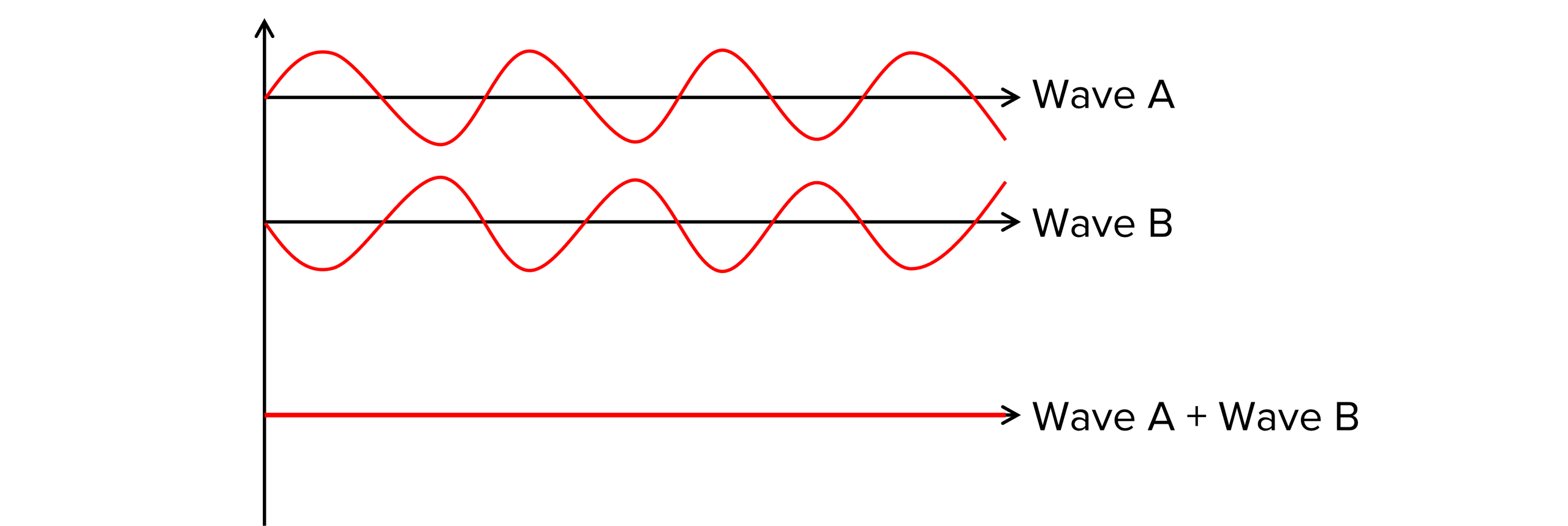
Destructive Interference – the diagram above shows destructive interference. The two waves at the bottom are in anti-phase and therefore destructively interfere. When the two wavelengths are combined, they cancel each other out forming a wave with zero amplitude throughout. 

Diffraction occurs any time a wave passes through a slit of past an object comparable to the wavelength of the wave. When the light from the diffraction grating or double slit is displayed in a screen, a distinctive pattern is shown.

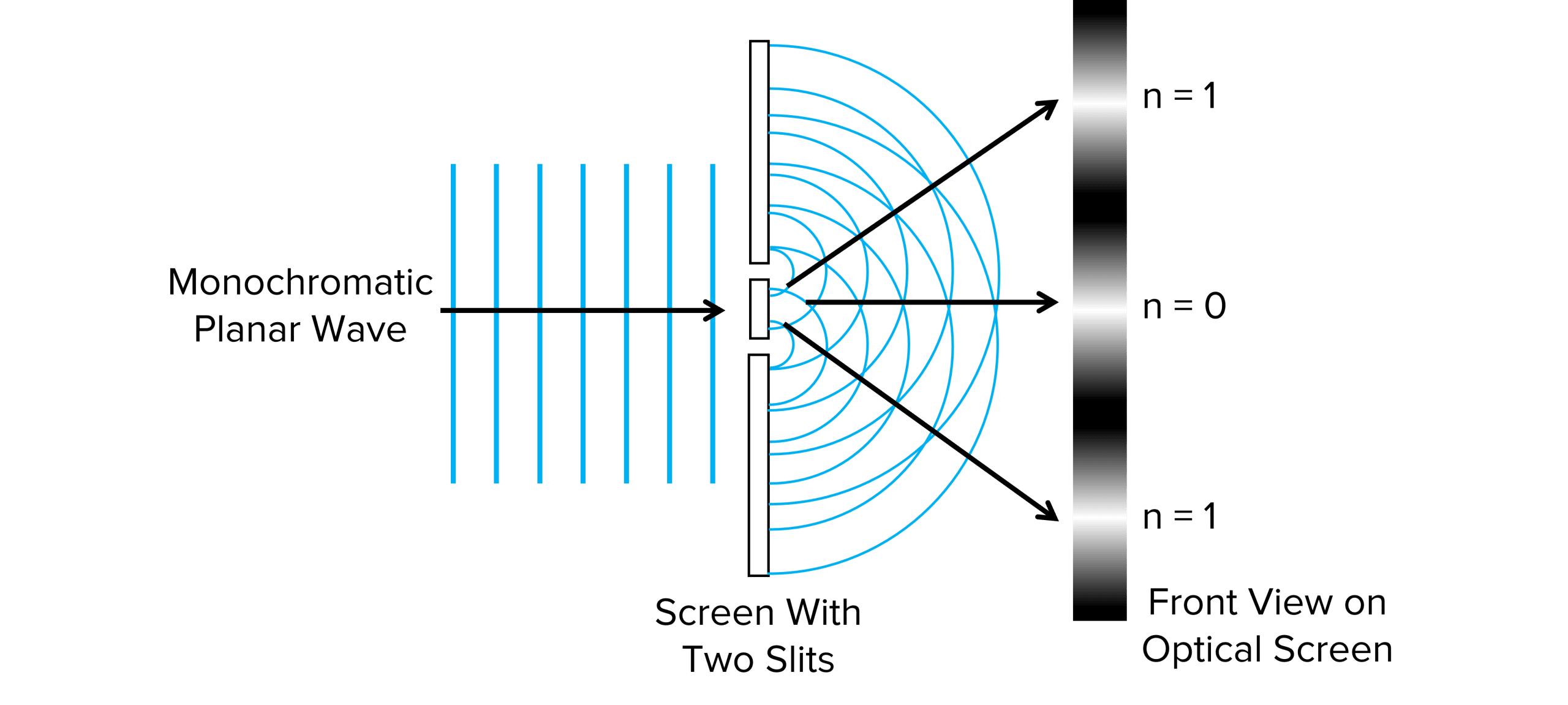
The light fringes displayed in the screen show areas where the waves have hit the screen with a whole number of wavelengths path difference. Therefore, constructive interference occurs, resulting in a bright maxima of light.

The dark fringes displayed in the screen show areas where the waves have hit the screen with a whole number and a half of wavelengths path difference. Therefore, destructive interference occurs, resulting in a dark minima of light.

The central bright fringe is the brightest of the maxima and is where there is no path difference. We label this n=0. Outwards from the centre in both directions, each bright fringe appears at each time the path difference is a whole number of wavelengths out. At n=1, the path difference is exactly one wavelength, n=2 is where the path difference is 2 wavelengths etc. The maxima gradually get dimmer as you move out from the centre due to the light intensity decreasing with distance

The fringe spacing equation allows us to calculate the distance between the centre of each bright fringe. The equation is:

w=\dfrac{\lambda D}{s}

• w= the fringe spacing in metres (m)
• \lambda= the wavelength in metres (m)
• D= the distance between the double slit and the screen in metres (m)
• s= the distance between the centre of the two slits in metres (m).

Doing the experiment:

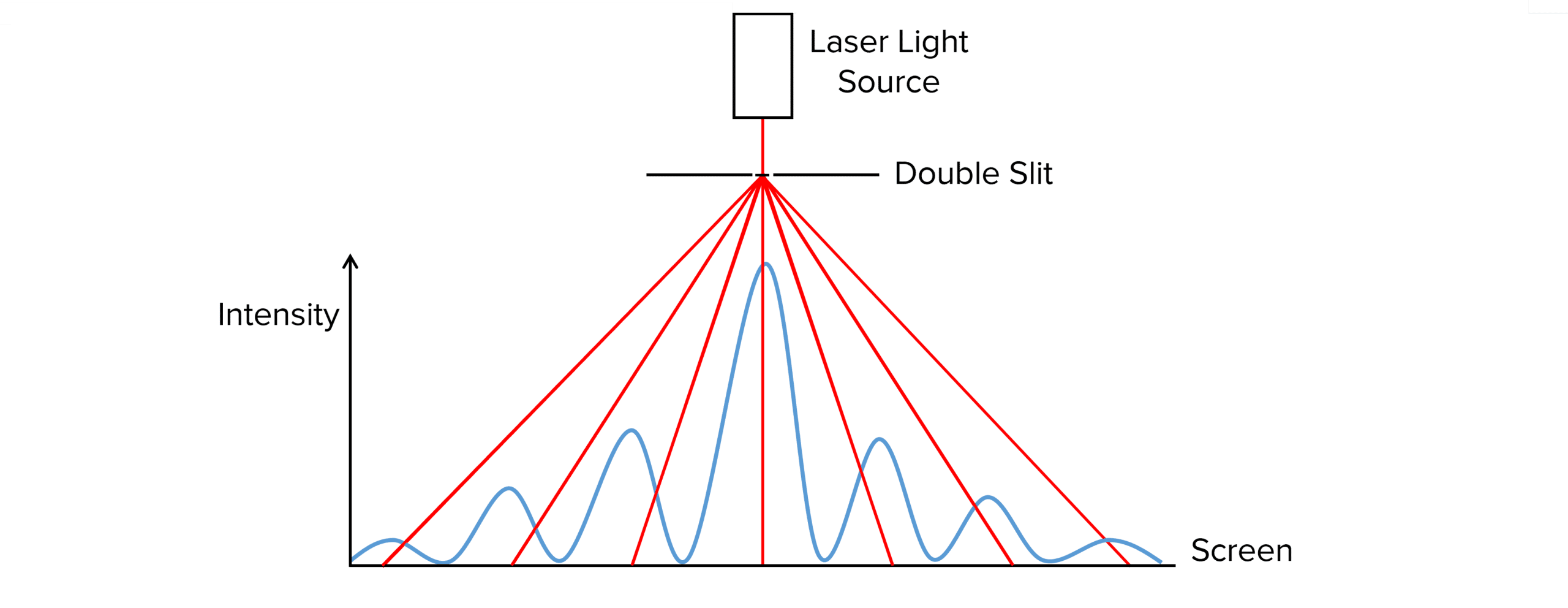
1. Set up the experiment as shown in the diagram above. 
2. Set the distance D at a fixed distance such as 1 \text{ m}. 
3. Ensure the room is dark and safety labels are put around the room before turning the laser on. 
4. Using vernier callipers, measure the fringe spacing of multiple bright fringes then divide by the number of fringes to give an accurate measure of w_1. 
5. Repeat the experiment, increasing the distance D by 0.1 \text{ m} each time.
6. Repeat until you have at least 3 sets of results for each value of D

Analysing the results:

The results collected can be compared to our expected results using the equation:

w=\dfrac{\lambda D}{s}

• w= the fringe spacing in metres \text{(m)}
• \lambda = the wavelength of light in metres \text{(m)}
• D = the distance between the double slit and the screen in metres \text{(m)}
• s= the distance between the centre of the two slits in metres \text{(m)}

A graph of w against D may be drawn where w is on the y-axis and D is on the x-axis. The graph formed will be a linear graph where the gradient is equal to \dfrac{\lambda}{s} . Therefore multiplying the gradient of the graph by the slit spacing (s) will give you the wavelength of light.

We may expect to have a degree of error in our measurements of small distances. This can be reduced by taking multiple readings and by measuring the fringe spacing over multiple fringes.