Stationary Waves

The most common way a stationary wave is formed between two fixed ends. An example of this is a string fixed at both ends, such as a guitar string. 

For a stationary wave to form, the waves travelling in each direction must be of the same frequency, wavelength and amplitude. 

A stationary wave stores energy unlike a progressive wave.

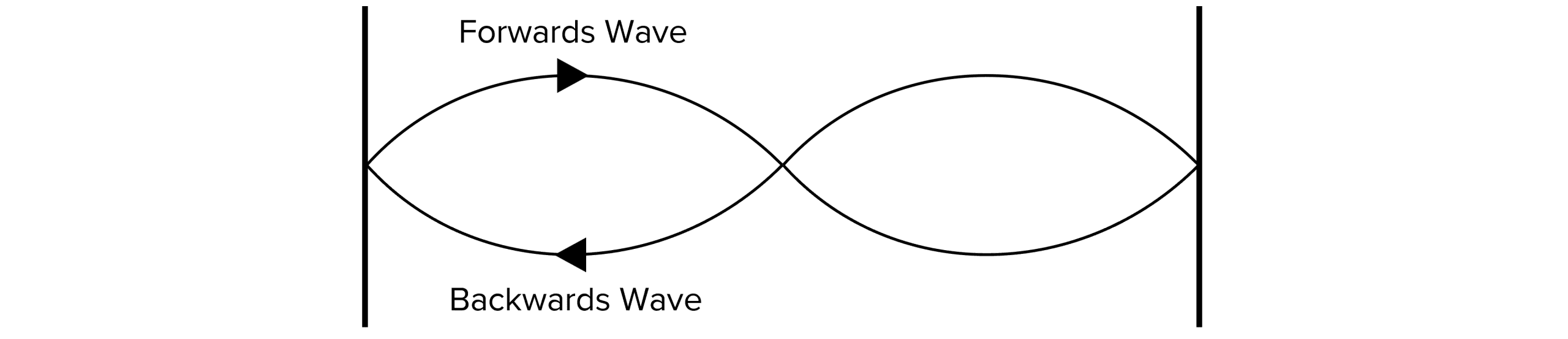
In the above example, a stationary wave is formed by a full wavelength in the forwards direction, followed by a full wavelength in the reflected direction. Both directions have the same amplitude, frequency and wavelength. We can also see that energy is stored within the system as it has no place to exit as the wave is bound between fixed points at each end of the wave.

These two terms are used a lot when discussing stationary waves, especially in written questions. They describe specific points on a wave. 

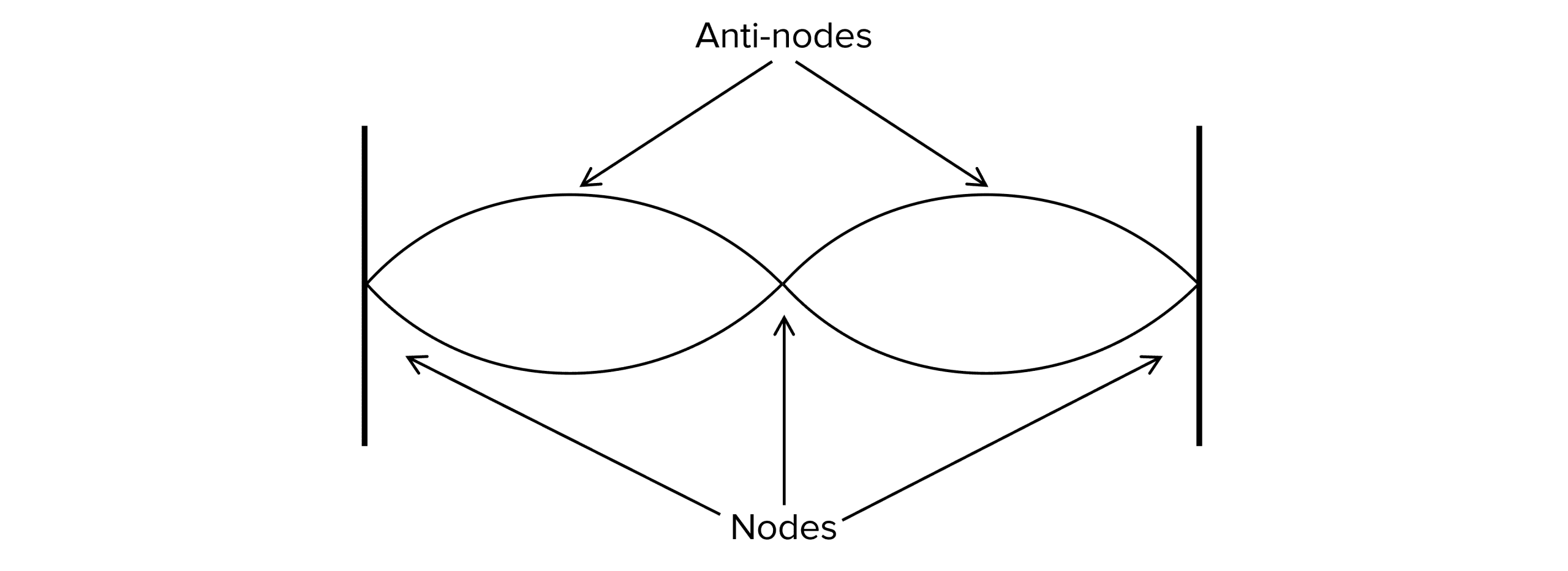
A node is a point on a stationary wave where there is zero amplitude.

An anti-node is a point on a stationary wave where there is maximum amplitude.

In a stationary wave with two closed ends (like the string above), the stationary wave will always have one more node than anti-node.

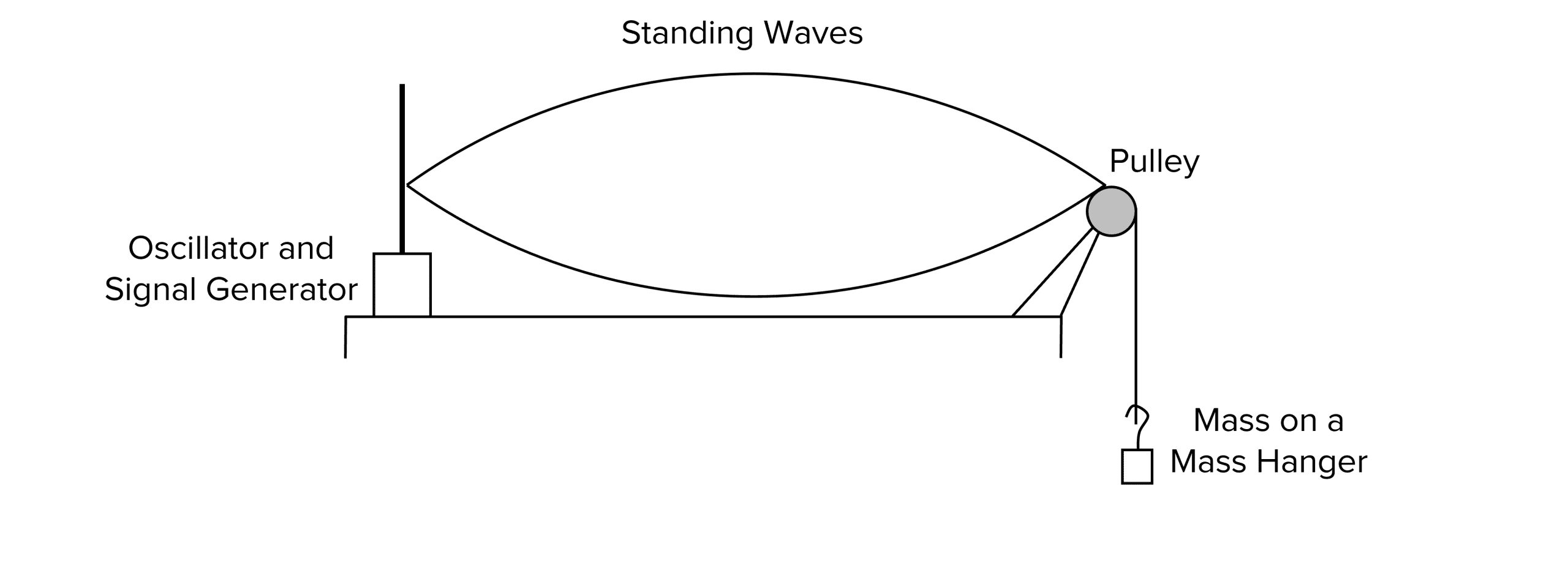
To produce a stationary wave in a string, the string must be held under tension. The equipment below may be used to keep the string under tension. It can also be used to investigate the effects of tension on the stationary wave produced.

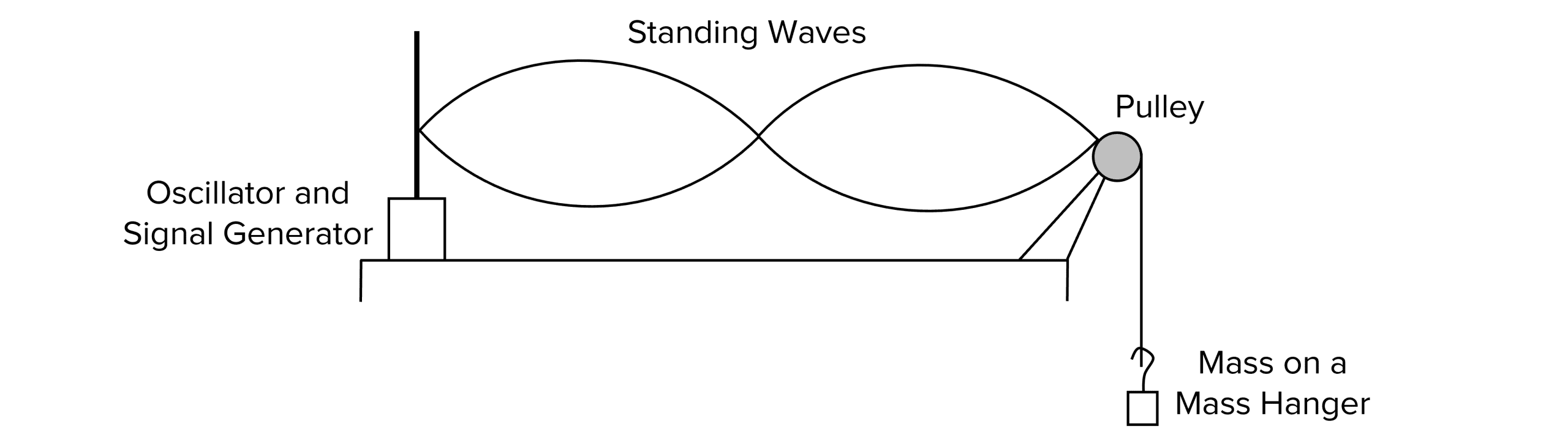
The oscillator can be set at different frequencies until a stationary wave is formed. The type of string, tension on the string and length between the two fixed points can be changed to create a variety of different investigations. 

It’s not just waves on a string that form stationary waves. Other examples include:

Microwaves

A similar experiment to the one above can be completed for microwaves. A microwave transmitter is used to emit microwaves at different frequencies. The microwave source is directed towards a shiny metal surface which acts as a reflector to reflect the microwaves back towards the transmitter. Finally, a microwave detector can be used to find the areas between the reflector and the source where there are nodes and anti-nodes to allow the waves to be sketched. 

Sound waves

Some musical instruments use sound to form stationary waves. These waves form inside a tube like that of a recorder or clarinet. If sound passes along the tube at the right frequencies, stationary waves form along the tube.

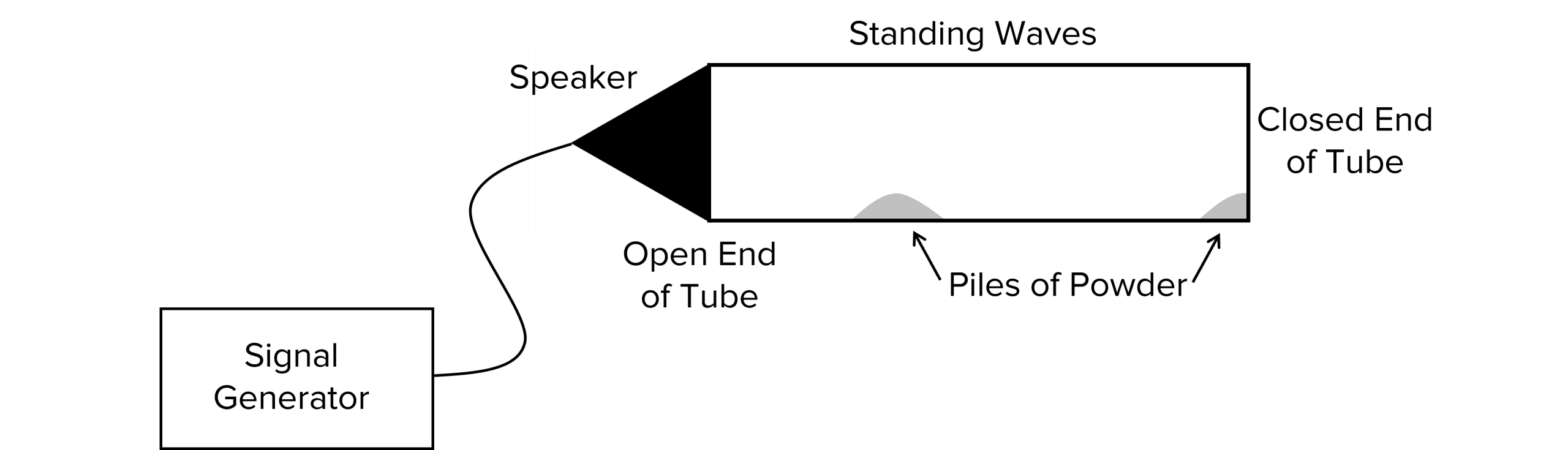
Because sound waves are not visible to the eye, a fine powder can be inserted into a tube in order to visualise the nodes and anti-nodes. When a stationary wave is formed, the powder moves into evenly distributed piles. These piles represent the nodes of the stationary wave. The frequency of the sound being produced can be adjusted to investigate how the position and number of piles changes. As the frequency increases, the number of nodes increases and the piles of powder move closer together.

Harmonics form along a wave when stationary waves are formed. The easiest way to observe this is along a string under tension but harmonics form in any stationary wave. 

The first harmonic forms in a stationary wave where the wave has two nodes and one anti-node. This is the first harmonic or the simplest stationary wave formed. This harmonic will form at specific frequencies depending upon the material, length and tension of the string.

For the first harmonic, if the length of the string is L, the wavelength would be 2L as the wave needs to reach the end of the string and reflect back again. The first harmonic is formed at the lowest frequency and as the frequency is increased, other harmonics are formed.

To calculate the frequency of the first harmonic we can use the wave speed equation, replacing the wavelength with \bold{2L}:

f = \dfrac{v}{2L}

• f= the frequency in hertz \text{(Hz)}
• v= the wave speed in metres per second \text{(ms}^{-1})
• L= the length of the string in metres \text{(m)}.

However, this equation is not the most useful on its own as it is hard to determine the speed of a wave along a string. Instead, we can combine this with another equation:

v=\dfrac{\sqrt{T}}{\mu}

• T= the tension in the string in newtons \text{(N)}
• /mu = the mass per unit length of the wire in kilograms per metre \text{(kgm}^{-1})

Substituting v into our original equation gives us:

f=\dfrac{1}{2L} \times \dfrac{\sqrt{T}}{\mu}

This is a much more usable equation as tension and mass per unit length are easily measured.

Harmonics form whenever a whole number of stationary waves form along the string. In the first harmonic one full wave is formed. We can use the general equation below to calculate the frequency of any harmonic:

f=\dfrac{1}{\lambda} \times \dfrac{\sqrt{T}}{\mu}

The second harmonic:

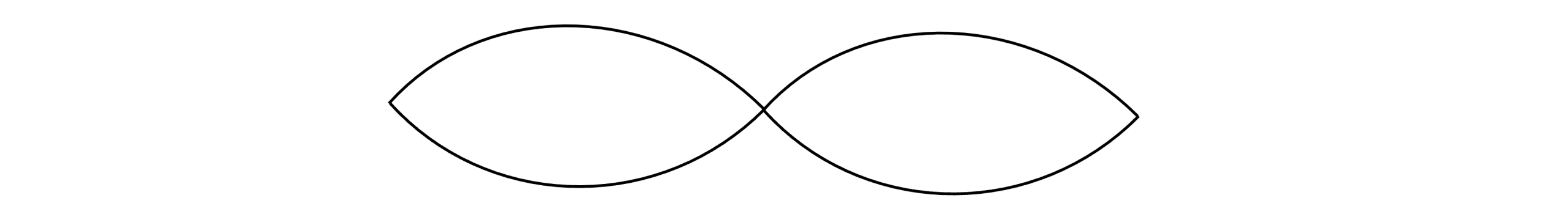
This produces \bold{3} nodes and \bold{2} anti-nodes. The wavelength is now  \dfrac{2L}{2} which simplifies to be L, and therefore the equation for the second harmonic is:

f=\dfrac{1}{L} \times \dfrac{\sqrt{T}}{\mu}

The third harmonic forms \bold{4} nodes and \bold{3} anti-nodes:

The wavelength is now \dfrac{2L}{3} and the equation for frequency becomes:

f=\dfrac{3}{2L} \times \dfrac{\sqrt{T}}{\mu}

You can now see a pattern between the harmonic number, wavelength and the number of nodes and anti-nodes.

Aim: To identify how the frequency of the first harmonic of a standing wave is affected by changing the length, tension or mass per unit length of a vibrating string.

Doing the experiment:

1. The equipment should be set up as shown in the diagram above.
2. Start with a low mass on the mass hanger. Calculate the tension using the equation, T=mg , where T is tension in newtons, m is mass in kilograms and g is gravitational field strength in newtons per kilogram. Record the tension in a results table.
3. Start the oscillator at a low frequency and gradually increase the frequency until the first harmonic can be observed. Record this frequency in your results table. 
4. Repeat with different masses hung on the mass hanger.
5. Repeat each mass at least three times and calculate the average frequency for each tension.