Moments

A LevelAS LevelAQA

Moments Revision

Moments

When a force acts on an object at a distance away from a pivot point, a turning effect is caused. These turning effects are known as moments. Moments cause an object to rotate about a pivot point. Understanding moments is crucial as their application is used in daily life.

Calculating Moments

A moment is a turning force and the SI unit for a moment is $\text{Nm}$ (Newton metre). A moment can be calculated using the following equation:

$\textcolor{aa57ff}{M = F \times d}$

$\textcolor{aa57ff}{M}$ is the moment in Newton-metres $\left(\text{Nm}\right)$
$\textcolor{aa57ff}{F}$ is the force in Newtons $\left(\text{N}\right)$
$\textcolor{aa57ff}{d}$ is the perpendicular distance from the pivot to the mass in metres $\left(\text{m}\right)$

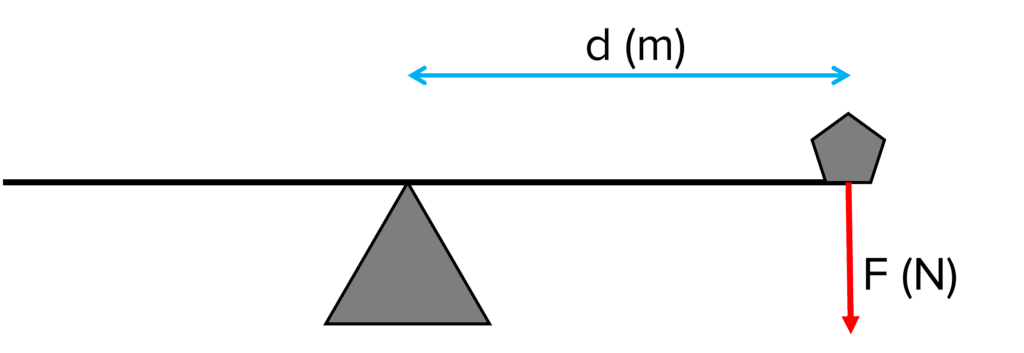
In this example on the right, the distance is easily measured from the centre of the pivot point to the centre of the force acting on it.

In this example we have not considered the mass of the beam holding the object but we will look at this in other examples.

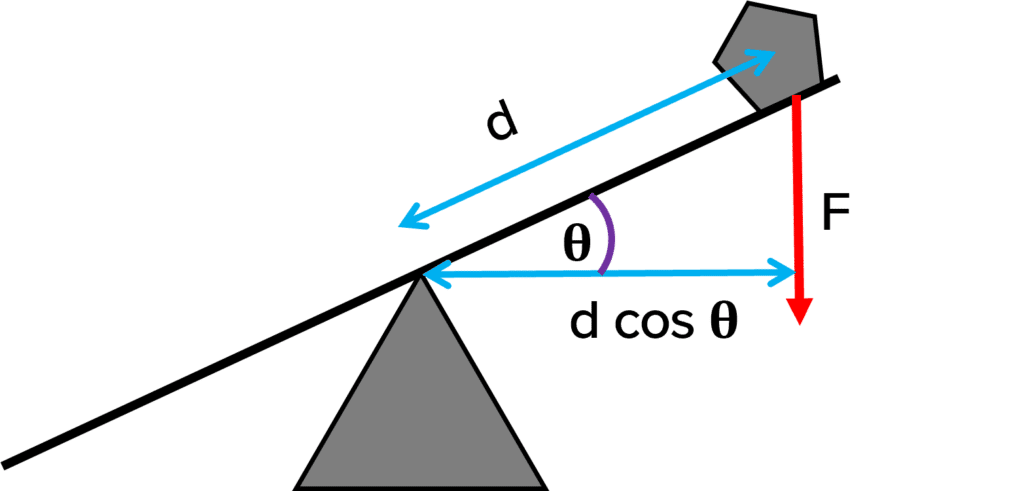
Sometimes we find examples where the rotating beam is at an angle to the horizontal, just as in the example on the right.

This time we are going to need to use some trigonometry to calculate the perpendicular distance from the pivot to the object:

$\textcolor{aa57ff}{\text{Moment} = F \times d \cos θ}$

Moments are all around us. We often consider the idea of moments without realising it. For example, if we are trying to release a tight bolt, we may pick a longer spanner. Or when opening a door, the door handle is on the far side of the door, furthest away from the pivot point to allow it to be opened easily.

In general, the greater the distance from the pivot, the greater the moment or turning effect as moments and the distance from the pivot are directly proportional.

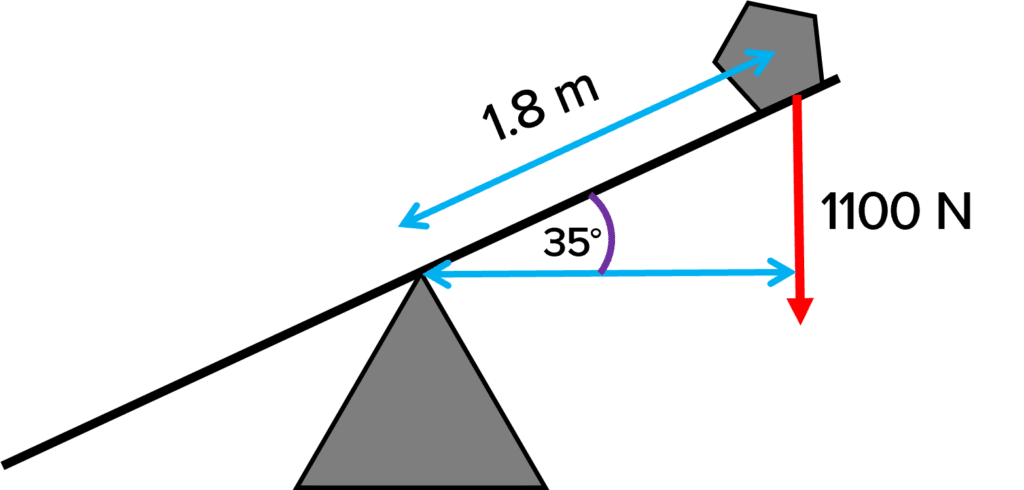
Example: Calculate the clockwise moment produced in the diagram on the right.

[3 marks]

$\text{Perpendicular distance} = d \cos θ = \boldsymbol{1.8 \cos 35 = 1.474} \: \textbf{m}$

$\text{Moment} = \text{force} \times \text{perpendicular distance} = \boldsymbol{1100 \times 1.474} = 1621.4 \: \text{Nm}$

$\text{Moment} = \boldsymbol{1600} \: \textbf{Nm} \left(2 \: \text{sf} \right)$

The Principle of Moments

Often moments are experienced in opposite directions. Picture the scenario below.

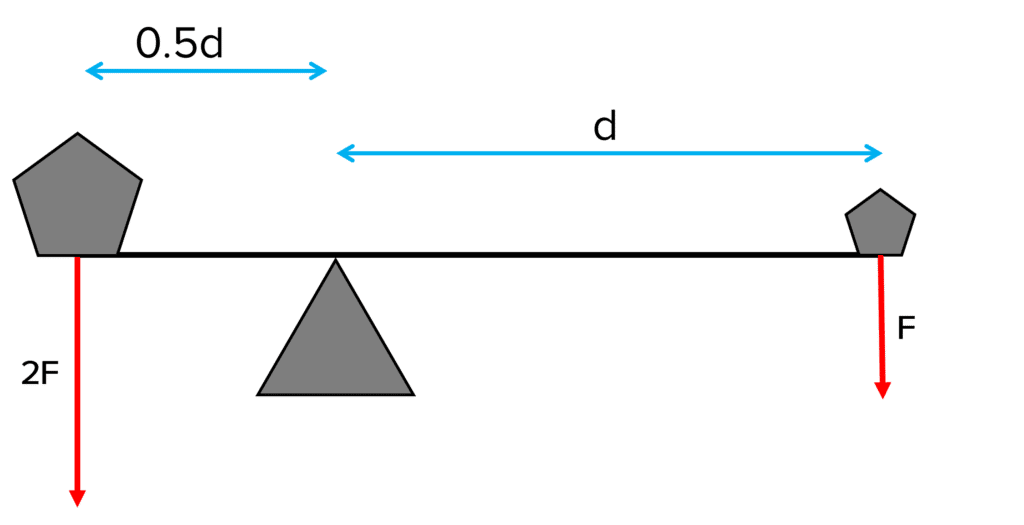
The object on the left is causing an anti-clockwise turning effect whilst the object on the right is causing a clockwise turning effect.

If these two moments are equal, we can say that the moments are in equilibrium.

If the moments are in equilibrium, no rotation will occur.

In our example the moments are in equilibrium. We can prove this:

$\text{Anti-clockwise moment} = 2F \times 0.5d = Fd$
$\text{Clockwise moment} = F \times d = Fd$

Therefore the moments are in equilibrium, because $\text{Anti-clockwise moment} = \text{Clockwise moment} = Fd$

Example: Two people are on opposite sides of a seesaw. Person A is $2 \: \text{m}$ away from the pivot and weighs $300 \: \text{N}$ . Person B sits $1.2 \: \text{m}$ away from the pivot. What must person B weigh if they are in equilibrium?

[3 marks]

$\text{Anti-clockwise moment} = \text{Clockwise moment}$

$F_A \times d_A = F_B \times d_B$

$\boldsymbol{300 \times 2 = F_B \times 1.2}$

So the force due to person B (in other words, their weight) is:

$F_B = \boldsymbol{\dfrac{300 \times 2}{1.2}}$

$F_B = \boldsymbol{500} \: \textbf{N}$

Couples

A couple is a pair of forces, acting in opposite directions which together cause a turning effect.

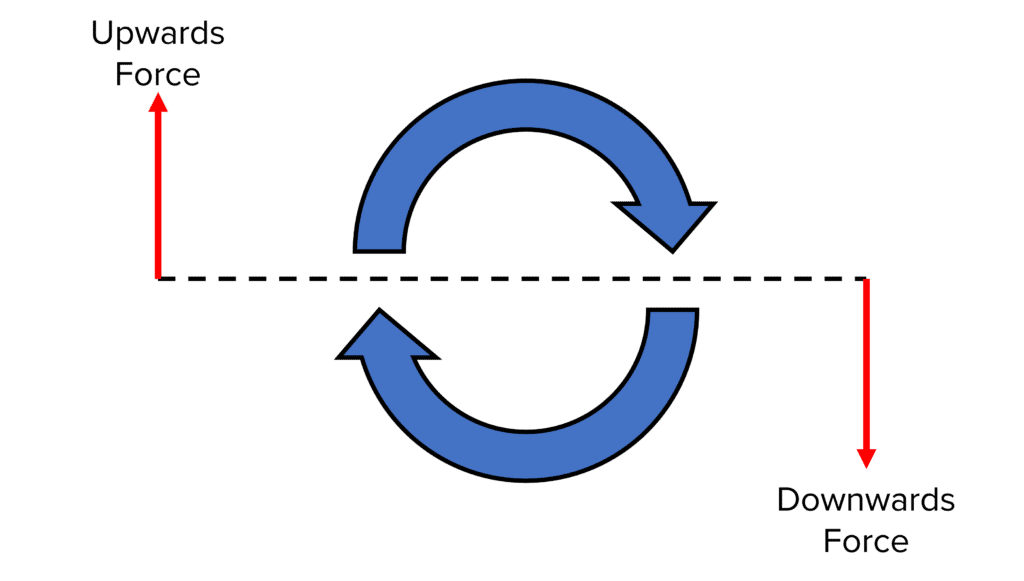
For the forces to be a couple, the forces must be coplanar and equal and opposite in magnitude. For forces to be coplanar, they must be acting in the same plane (but may be acting opposite in direction).

This pair of forces can cause a rotation without the need of a pivot. As the forces are equal and opposite, the resultant force is zero. Therefore there is no net movement other than the rotation of the object.

Centre of Mass

The centre of mass of an object is the point at which all of the object’s mass could be considered to act. For our calculations, this allows us to consider objects as point masses where the full mass of the object acts in one position.

For an object of uniform density (has the same density throughout), its centre of mass is at the centre of the object.

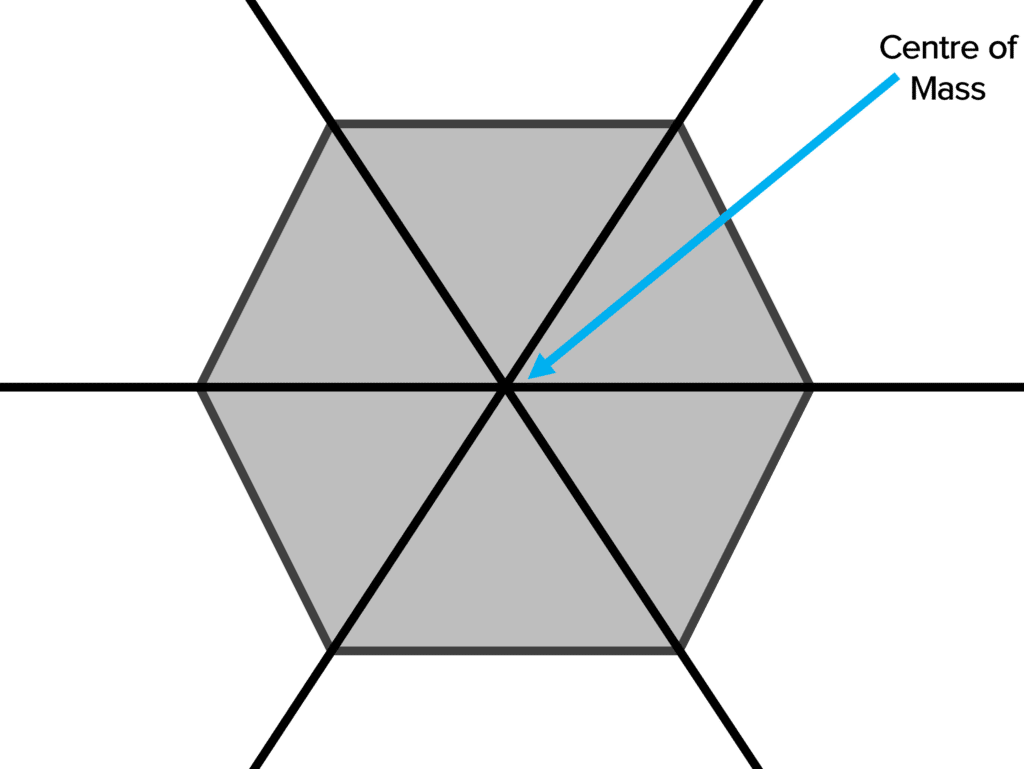
If the object is symmetrical this can easily be found. If you take more than one line of symmetry, the centre of mass will be at the point where the lines of symmetry intersect.

The centre of mass of this regular hexagon can be seen where all of its lines of symmetry meet.

The centre of mass for an Irregular shaped object is trickier to identify:

To find the centre of mass, you take the object and hang it from a fixed point next to a plum line.
Next, draw a straight line where the plumb line touches the object.
Repeat this by hanging the object from another point. The centre of mass is where the lines intersect.

Stability

For objects that can change shape, like people, the centre of mass will move depending on their position. As a standing person bends their knees, their centre of mass becomes closer to the ground. The closer the centre of mass is to the ground, the more stable you are.

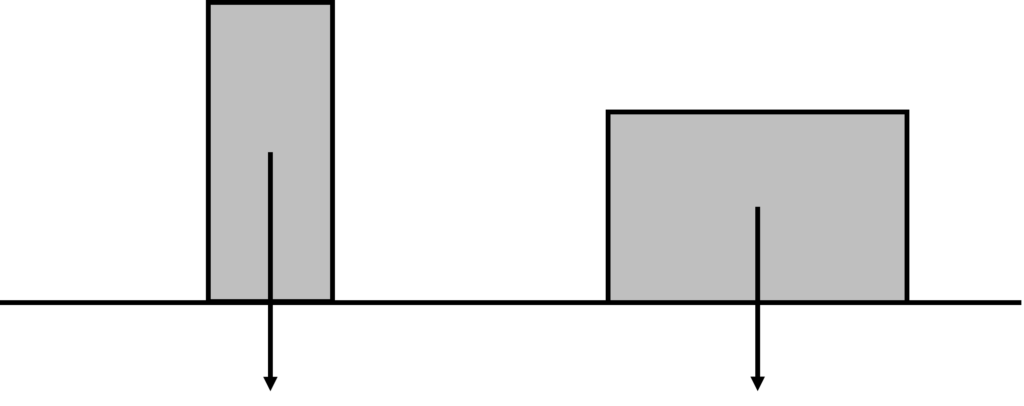
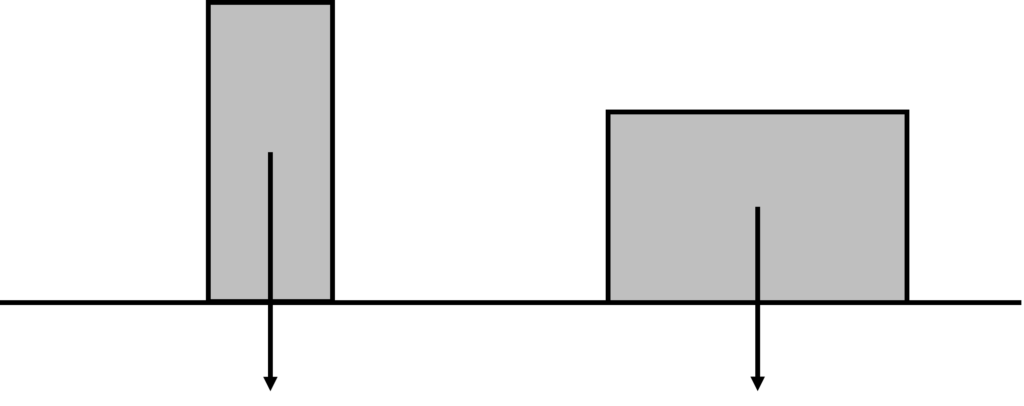
In the diagram on the right, both objects above are currently stable. This is because their centre of mass (indicated by the arrows) are acting above the base of the object. However, we would consider the right hand object to be more stable as it would take more effort to move the object enough so that it’s centre of mass moved outside of its base:

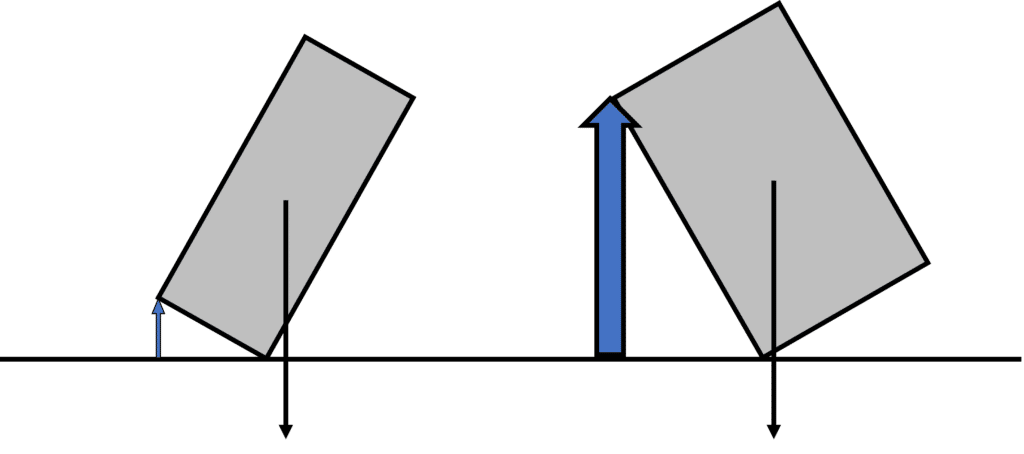
Both objects are now unstable as their centre of mass is no longer above their base. However, it has taken a much greater movement to cause the left object to become unstable when compared to the right object. This is because of the large base of the right hand object.

Moments Example Questions

Question 1: Calculate the resultant moment from the diagram below:

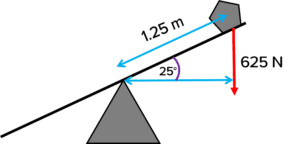
[3 marks]

\begin{aligned} \text{Perpendicular distance} &= \boldsymbol{1.25 \cos 25 = 1.13} \: \textbf{m} \\ \text{Moment} &= \boldsymbol{625 \times 1.13 = 708} \: \textbf{Nm} \end{aligned}

Save your answers with

Gold Standard Education

Question 2: Two people are on opposite sides of a seesaw. Person A is $1 \: \text{m}$ away from the pivot and weighs $500\: \text{N}$ . Person B weighs $700\: \text{N}$ . How far from the pivot would person B need to sit to ensure they are in equilibrium?

[3 marks]

\begin{aligned} \text{Anti-clockwise moment} &= \text{Clockwise moment} \\ F_A \times d_A &= F_B \times d_B \\ \boldsymbol{500 \times 1} &\boldsymbol{= 700 \times d_B} \\ \boldsymbol{d_B }&\boldsymbol{= \dfrac{500}{700}} \\ \boldsymbol{d_B} &\boldsymbol{= 0.7} \: \textbf{m} \end{aligned}

Save your answers with

Gold Standard Education

Question 3: Using your knowledge of the centre of mass, explain why would a forklift truck be better carrying its load close to the ground, rather than higher up in the air.

[2 marks]

As the mass of the load is lowered towards the ground, the centre of mass of the load and the truck moves towards the ground. This improves the stability of the load and forklift truck.

Save your answers with

Gold Standard Education