Revise
Bulk Properties of Solids
Bulk Properties of Solids Revision
Bulk Properties of Solids
For this section we will look at the bulk properties that make up solids. “Bulk” just means looking at a materials properties overall, as opposed to at an atomic level. Specifically we will look at density and how the solids behave when they are exposed to compressive or extensive forces.
Density
Density is defined as the mass per unit of volume of a material. When calculating density it is important to try to stick with standard units. Therefore, most commonly you will see density expressed with the units \text{kgm}^{-3}. However, you may also see density expressed on other units such as \text{gm}^{-3} or \text{gcm}^{-3}.
The equation to calculate density is:
\rho = \dfrac{m}{V}
- \rho is the density in kilograms per metres cubed\left(\text{kgm}^{-3}\right)
- m is the mass in kilograms \left(\text{kg}\right)
- V is the volume in metres cubed \left(\text{m}^3\right)
A material with high density has a large amount of mass concentrated in a small volume such as a brick or cube of lead.
A material with lower density has a smaller amount of mass for the same amount of volume such as a sponge or a balloon filled with air.
Example: A cylinder of a gas of volume 1.5 \: \text{m}^3 and mass 0.02 \: \text{kg}. What is the density of the cylinder?
[1 mark]
\rho = \dfrac{m}{V}
\rho = \dfrac{0.02}{1.5} = 0.013 \: \text{kgm}^{-3}
Hooke’s Law
A material obeys Hooke’s law if the extension or compression of the material is directly proportional to the force applied to it \left( F \propto x \right). So, for example, when the force applied to the material doubles, the extension of the material doubles.
This can be given in the equation:
F = kx
- F is the force applied to the spring in Newtons \left(\text{N}\right)
- k is the spring constant in Newtons per metre \left(\text{Nm}^{-1}\right)
- x is the extension of the spring in metres \left(\text{m}\right)
The spring constant \left(Nm^{-1}\right) is a property of a material. It is a way of describing how easy or hard it is to stretch or compress the object.
A high spring constant means a large force is required for a small extension or compression.
A low spring constant means a bigger force is required for the same amount of extension.
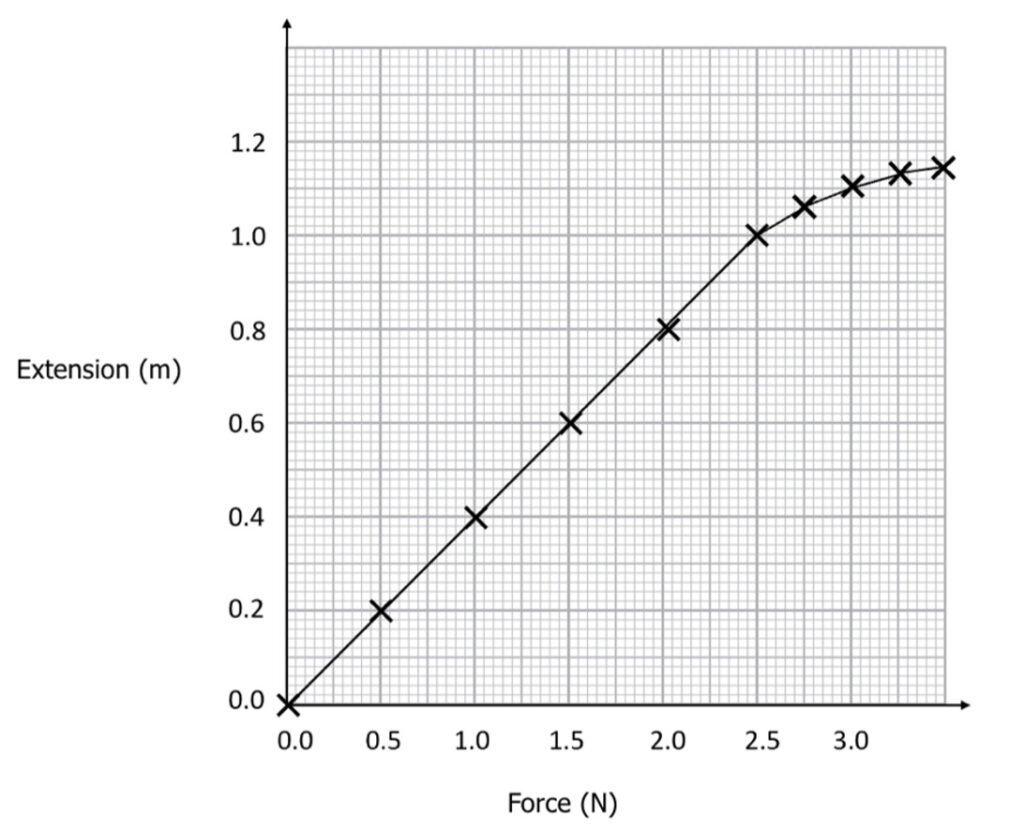
On a force-extension graph, Hooke’s law can be seen as the linear section of the graph. We can see this on the graph here:
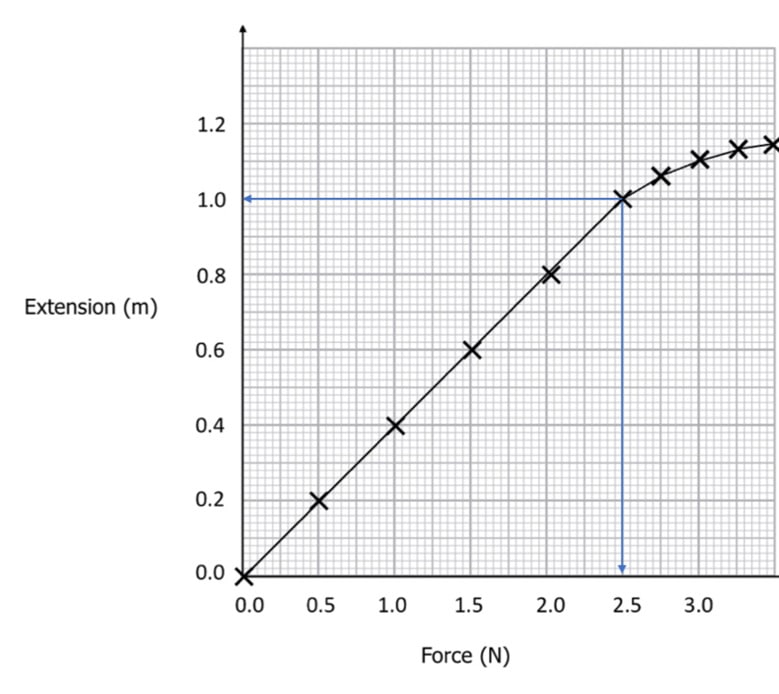
The graph can be used to calculate the spring constant.
- We know that \text{Spring constant} = \dfrac{\text{Force}}{\text{Extension}}.
- The gradient of the graph is \dfrac{\text{Extension}}{\text{Force}}.
- So to find k, we calculate \dfrac{1}{\text{gradient}} = \dfrac{\text{Force}}{\text{Extension}}.
- \text{Spring constant}, \: k = \dfrac{2.5-0}{1-0} = 2.5 \: \text{Nm}^{-1}
However, not all materials obey Hooke’s law for all sizes of force. Notice in the above graph, after the linear section of the graph the line begins to curve. At this point the material is no longer obeying Hooke’s law. We say that the material has reached its limit of proportionality. Beyond this point the material will no longer return to its original shape.
Elastic behaviour: this is shown by the linear section of the graph. Elastic behaviour results in the material returning to its original shape.
Plastic behaviour: this is shown by the curved section of the graph. The material will no longer return to its original shape. It has been plastically deformed.
Springs and Energy
It is important to note how energy transfers occur in a spring with a load place on it. Say a mass is place on a spring. This mass is a force doing work in the spring. This work done is stored as elastic potential energy. This can then be converted into other forms. For example, if the mass is removed then some of this elastic potential energy will be converted to kinetic energy and the spring will move.
Bulk Properties of Solids Example Questions
Question 1: A cube of an unknown material has a density of 0.5 \: \text{kgm}^{-3} and a mass of 0.1 \: \text{kg}. Calculate the volume of the cube.
[2 marks]
Rearranges to:
\begin{aligned} V &= \dfrac{m}{\rho} \\ \\ V &= \dfrac{0.1}{0.2}= 0.2 \: \text{m}^3 \end{aligned}
Question 2: Calculate the spring constant of this spring using the graph given below:
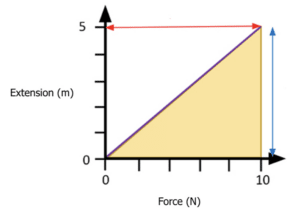
[2 marks]
Question 3: Describe the difference between elastic deformation and plastic deformation and how would you identify each in a force-extension graph?
[4 marks]
- Elastic deformation occurs when a spring extends but returns back to its original length and shape once the load is removed. This is identified by the straight line section (before the limit of proportionality)of the graph.
- Plastic deformation occurs when a spring extends but does not return back to its original length and shape once the load is removed. This is identified by the curved line section of the graph (after the limit of proportionality).
