Young's Modulus
Young's Modulus Revision
Young’s Modulus
This section looks at some other terms that can be used to describe and quantify the effects of a force upon a material. We will look at stress, strain and Young’s modulus and how they are calculated.
Tensile Stress and Strain
For a material put under load, the tensile stress is equal to the force applied per unit of cross-sectional area. Tensile forces are applied to an object when a force is applied in opposite directions to each end of the object, causing a stretching effect.
Tensile stress can be calculated using the equation:
\sigma = \dfrac{F}{A}
- \sigma is the tensile stress in pascals \left(\text{Pa}\right)
- F is the force in Newtons \left(N\right)
- A is the cross-sectional area in metres squared \left(m^2\right)
The tensile strain of an object under load is defined as the extension per unit of original length. As an equation, this is written as:
\epsilon = \dfrac{\Delta L}{L}
- \epsilon is the tensile strain of the material. It is unitless.
- \Delta L is the change in length of the material in metres \left(m\right).
- L is the original length of the material in metres \left(m\right).
Example: A wire of radius 0.01 \: \text{m}, original length of 2 \: \text{m} is put under a tensile force of 75 \: \text{N}. The wire extends by 1.5 \: \text{m}. Calculate the tensile stress and strain of the wire.
[2 marks]
Finding the stress:
\begin{aligned}\sigma &= \dfrac{F}{A} \\ \\ \sigma &= \dfrac{75}{\pi \times 0.01^2} = \boldsymbol{238853.5} \: \textbf{Pa} \: \text{or} \: \boldsymbol{0.24} \: \textbf{MPa} \end{aligned}
Finding the strain:
\begin{aligned} \epsilon &= \dfrac{\Delta L}{L} \\ \\ \epsilon &= \dfrac{1.5}{2} = \boldsymbol{0.75} \end{aligned}So the tensile stress =\boldsymbol{0.24} \: \textbf{MPa} and the tensile strain = \boldsymbol{0.75}
Stress-Strain Graphs
A lot can be interpreted when stress is plotted against strain in a stress-strain graph. Here is an example:
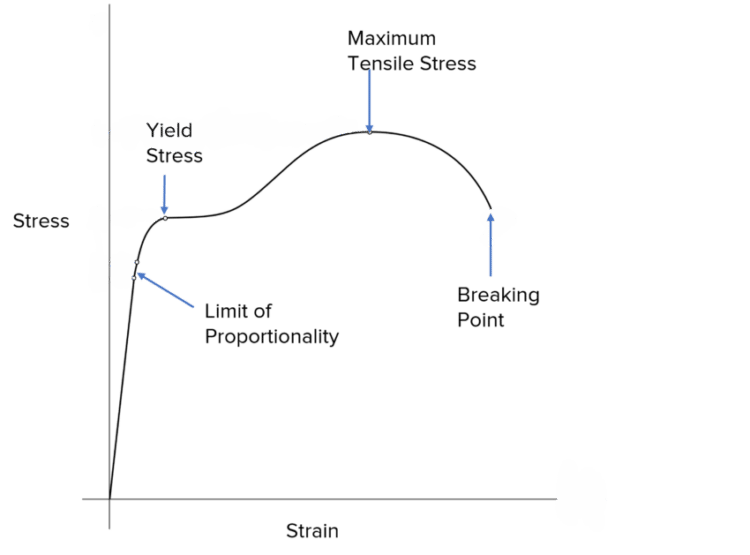
As labelled, there are several distinguishable features of a stress-strain graph:
Limit of proportionality – the point at which the graph first starts to curve. This shows the point where the material no longer obeys Hooke’s law.
Yield strength– this is the first turning point of the graph and represents where the material yields. At this point an increase in strain can be seen without an increase in stress showing the material yielding.
Maximum tensile stress – the highest point on the graph. This shows the maximum force per unit cross sectional area.
Breaking point – the endpoint of the curve. At this point the material has snapped and therefore has no stress being applied.
On a stress-strain graph a brittle material could be identified as a material that has no or very little curved area of the graph. It would also tend to be displayed as a steep line with very low maximum strain as brittle materials do not stretch or bend very well without snapping. A ductile material would be represented by a long curved graph as ductile materials can be stretched well without.
Elastic Strain Energy
The elastic strain energy is the energy stored in the material due to the work being done on the material in stretching it. The elastic strain energy can be calculated in two ways:
First method:
- If the material obeys Hooke’s law (anytime the graph is linear) we can use an equation:
\text{Elastic Strain Energy} = \dfrac{1}{2} F \Delta L or \text{Elastic Strain Energy} = \dfrac{1}{2} k \Delta L^2
- F is the force applied in Newtons \left(\text{N}\right).
- \Delta L is the change in the length in metres \left(\text{m}\right)
- k is the spring constant in Newtons per metre \left(\text{Nm}^{-1}\right)
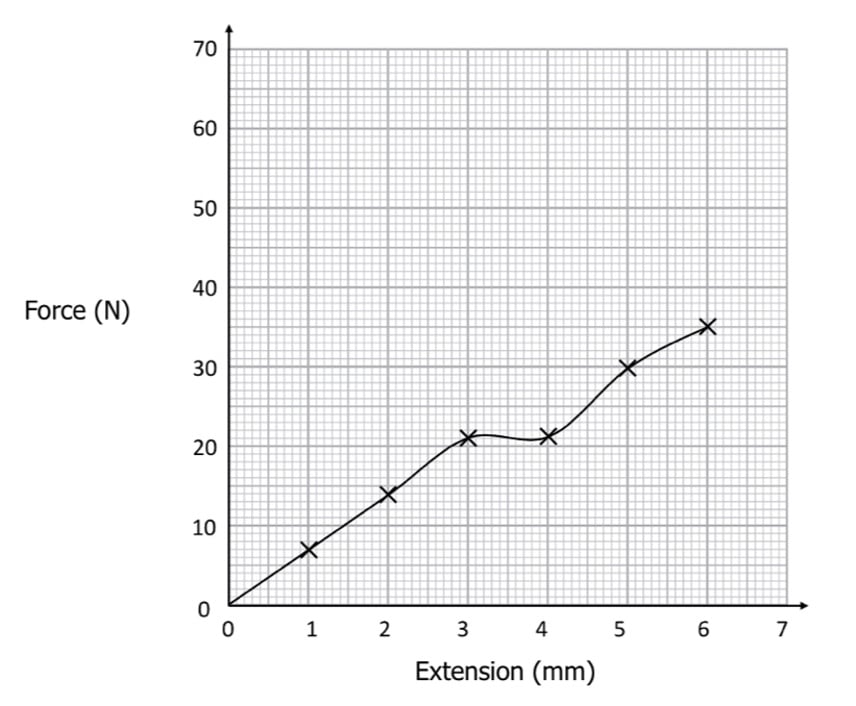
Example: Using the graph, calculate the elastic strain energy in the part of the graph that obeys Hooke’s Law
[1 mark]
The linear section is approximately from 0 \: \text{mm} to 2 \: \text{mm} of extension. So this part of the graph obeys Hooke’s Law.
\text{Elastic strain energy} = \dfrac{1}{2} F \times \Delta L
\text{Elastic strain energy} = \dfrac{1}{2} \times 14 \: \text{N} \times 0.002 \: \text{m} = \boldsymbol{0.0014} \: \textbf{J}
Second method:
The second method below can be applied to both instances where a material obeys Hooke’s law or if it has passed its limit of proportionality and is behaving plastically.
- The elastic strain energy can be determined by calculating the area under a Force-extension graph.
Example: Estimate the total amount of elastic strain energy stored in the material over the whole graph.
[4 marks]
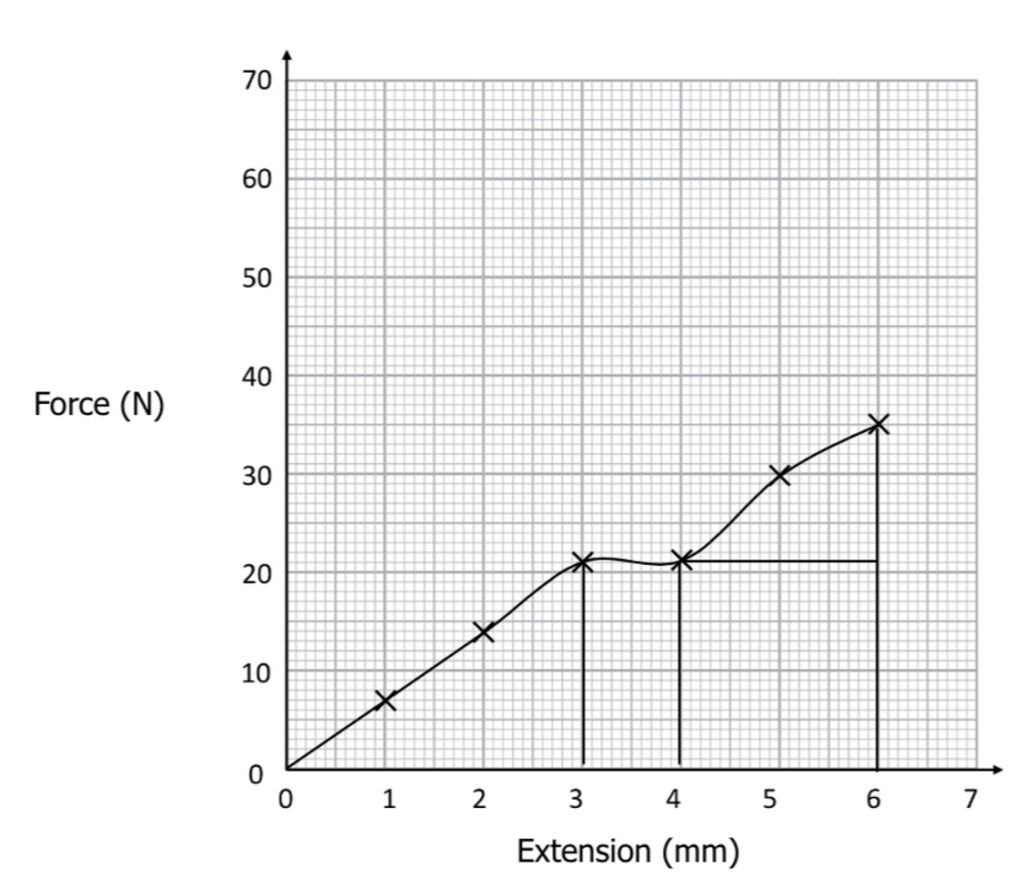
Firstly, split the graph into easy to calculate sections.
Estimate the area of each section:
From \boldsymbol{0-20} \: \textbf{N}: 0.5 \times 20 \times 0.003 = \boldsymbol{0.03} \: \textbf{J}
At \boldsymbol{20} \: \textbf{N}: 20 \times 0.001 = \boldsymbol{0.02} \: \textbf{J}
From \boldsymbol{20 – 35} \: \textbf{N}: \left(21 \times 0.002\right) + \dfrac{1}{2} \left(14 \times 0.002\right) = \boldsymbol{0.056} \: \textbf{J}
Whole area = 0.03 + 0.02 + 0.056 = \boldsymbol{0.106} \: \textbf{J}
Young’s Modulus
Another quantity that can be calculated using stress and strain is the Young’s modulus. Young’s modulus is the ratio of tensile stress divided by tensile strain. This can be written in the form:
\text{Young's Modulus} = \dfrac{\text{Stress}}{\text{Strain}}
We can take our equations from the previous sections and write this as:
\text{Young's Modulus} = \dfrac{F/A}{\Delta L / L} = \dfrac{FL}{A \Delta L}
Example: The Young’s modulus of aluminium is 68 \: \text{GPa}. If the tensile stress on aluminium is 15 \: \text{GPa}, what is the strain?
[2 marks]
\text{Young's Modulus} = \dfrac{\text{Tensile Stress}}{\text{Tensile Strain}}
\textbf{Tensile Strain} = \dfrac{\textbf{Tensile Stress}}{\textbf{Young's Modulus}}
\text{Tensile Strain} = \dfrac{68 \times 10^9}{15 \times 10^9} = \boldsymbol{4.5}
Required Practical 4
Determination of the Young’s modulus of different pieces of wire.
This experiment can be carried out using any type of wire. The experiment may also be done using a vertical piece of wire suspended from the ceiling.
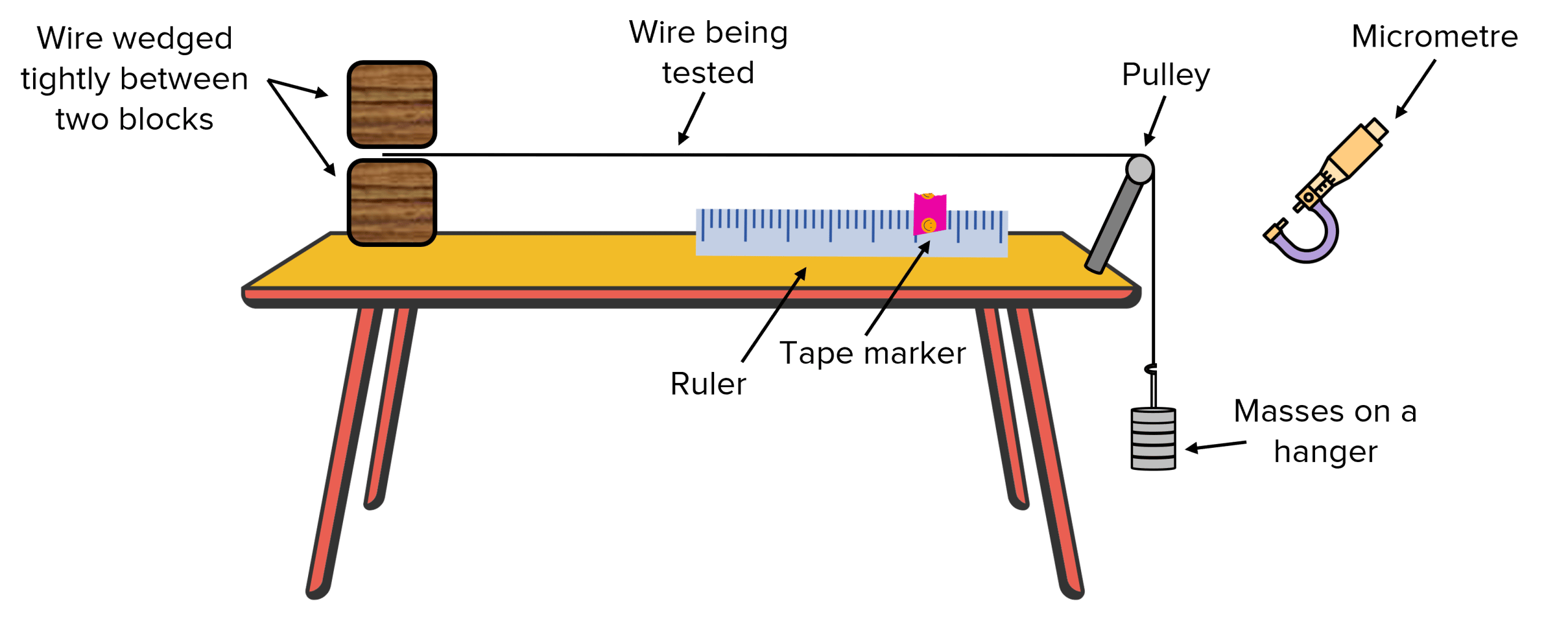
Doing the experiment:
- Firstly, before any equipment is set up, the diameter of the wire needs to be measured. A micrometer can be used for this. Measure the diameter of the wire in three different places and orientations along the wire before taking an average. Be careful not to squash the wire by over tightening the micrometer.
- Set up the equipment as shown in the diagram above.
- Make the wire tight but with no mass on the mass hanger and measure the original length of the wire. Mark a point on the wire using a marker. This could be a pointed piece of tape that points downwards to the ruler.
- Begin by adding a 100 \: \text{g} mass onto the mass hanger. Record this mass and also record the extension by observing how far the marker has moved from the original position. Record the extension in metres.
- Repeat the above step 10 times until 1 \: \text{kg} has been added.
Analysing the results:
To analyse the results, all masses must be converted to newtons by multiplying by g \left(9.81 \: \text{N/kg}\right) and all lengths/diameters must be converted to metres.
Young’s modulus is given by the equation:
\text{Young's Modulus} = \dfrac{\text{Stress}}{\text{Strain}} = \dfrac{FL}{A \Delta L}
where F is the force applied to the wire, L is the original length of the wire, A is the cross-sectional area of the wire and \Delta L is the extension of the wire.
In our experiment we have recorded the force on the wire \left(F\right) and the corresponding extension of this wire \left(\Delta L\right). Therefore, we can plot a graph of force on the y-axis and extension on the x-axis:
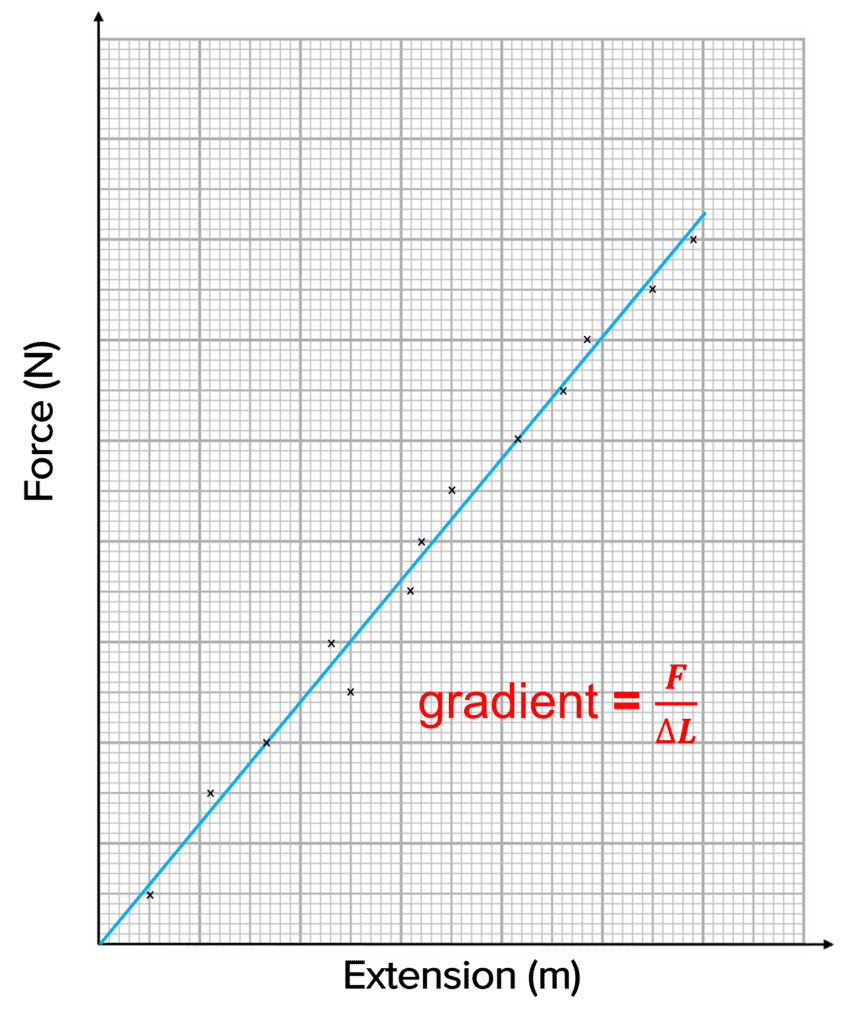
The gradient of this graph will give \dfrac{F}{\Delta L}.
Our Young’s Modulus equation is :
\text{Young's Modulus} = \dfrac{FL}{A \Delta L}
So we can rewrite this as:
\text{Young's Modulus} = \text{gradient} \times \dfrac{L}{A}
So to work out our Young’s Modulus, we just multiply the gradient of the graph by the original length and divide by the cross-sectional area.
You should have measured the diameter of your wire in the experiment. We can use this and the area of a circle equation A = \pi r^2 to calculate the cross-sectional area of the wire, A.
Young's Modulus Example Questions
Question 1: Describe the stress-strain graph you would expect to see for a brittle material.
[2 marks]
A brittle material is a material that cannot stretch or bend very much without breaking.
Therefore, the stress strain graph will mostly be linear with a low breaking stress and strain.
Question 2: Young’s modulus for aluminium is 70 \: \text{GPa} and 170 \: \text{GPa} for Iron. What does this tell you about these two materials?
[2 marks]
Young’s modulus is a measure of how good a material is at coping with a high load, without deforming.
Therefore, as iron has a much higher Young’s modulus, we would expect iron to be better at withstanding high stresses whilst deforming very little compared to aluminium.
Question 3: Young’s modulus for steel is 110 \: \text{GPa} and can withstand a tensile strength of 1.8 \: \text{GPa}. Calculate the strain when the steel undergoes this tensile strength.
[2 marks]
Young's Modulus Worksheet and Example Questions
Materials Questions
A LevelOfficial MMEYou May Also Like...
MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.
