Fields
Fields Revision
Fields and Gravitational Field Strength
GCSE Physics introduced the idea of forces and force fields. In this section we begin looking at the different types of field you will encounter.
Fields
A force field (such as a magnetic field or electric field) is the area in which a body will experience a force. The force will be a non-contact force as no contact is needed between the field and the body. Below are some examples of some contact and non-contact forces:
Contact Forces:
- Push and pull
- Tension
- Friction
- Air resistance
- Water resistance
- Normal contact force
Non-contact Forces:
- Electrostatic forces
- Magnetic force
- Gravitational force (Weight)
Only non-contact forces can have force fields.
Drawing Force Fields
As with any force, when drawing force fields, it is important to show the magnitude and direction of the force as forces are vector quantities. Some important things to remember when drawing field lines are:
- Circular or spherical objects like the Earth can be considered as a point mass/charge.
- A uniform force field is one in which the field is equal at all points within the field.
- The closer the field lines, the stronger the field.
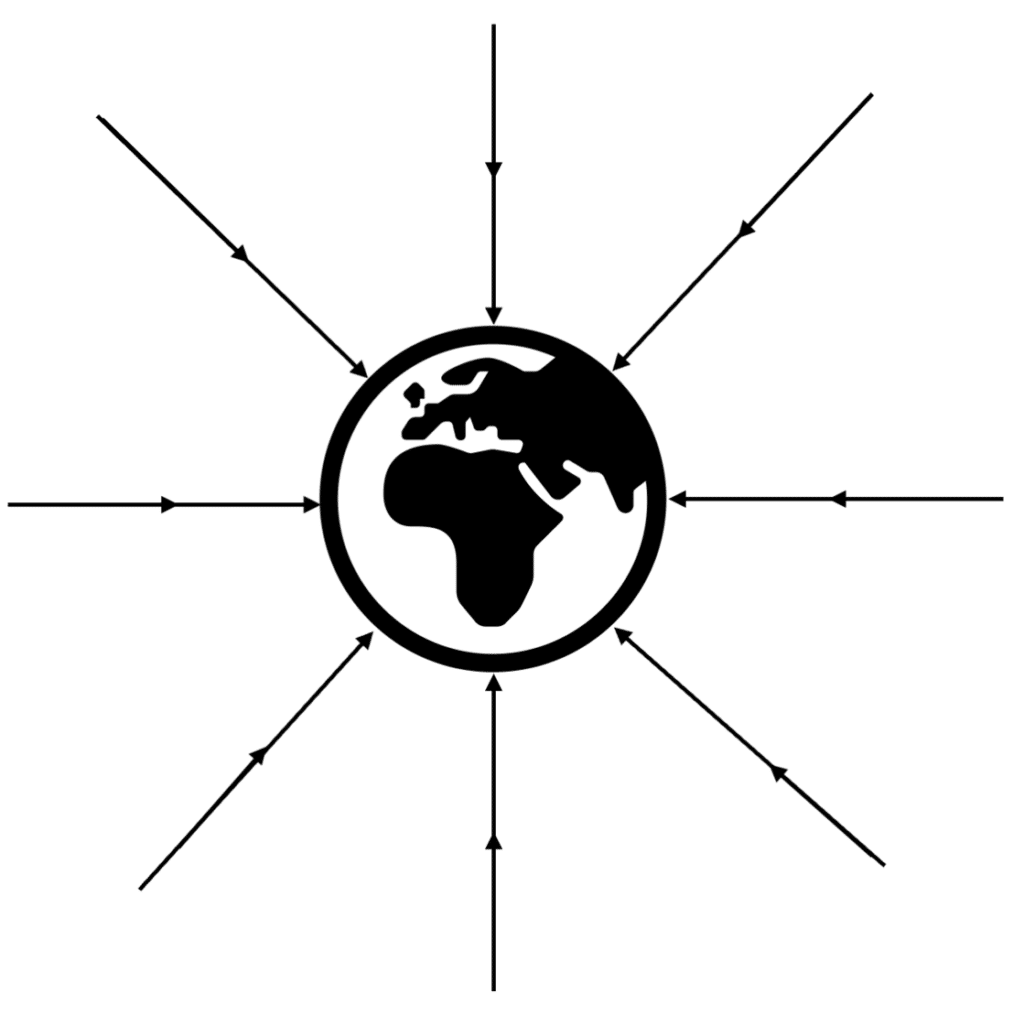

On the right, we can see a representation of the gravitational field around the Earth.
We can see that the field lines are non-uniform as the distance between the field lines varies with distance from the centre.
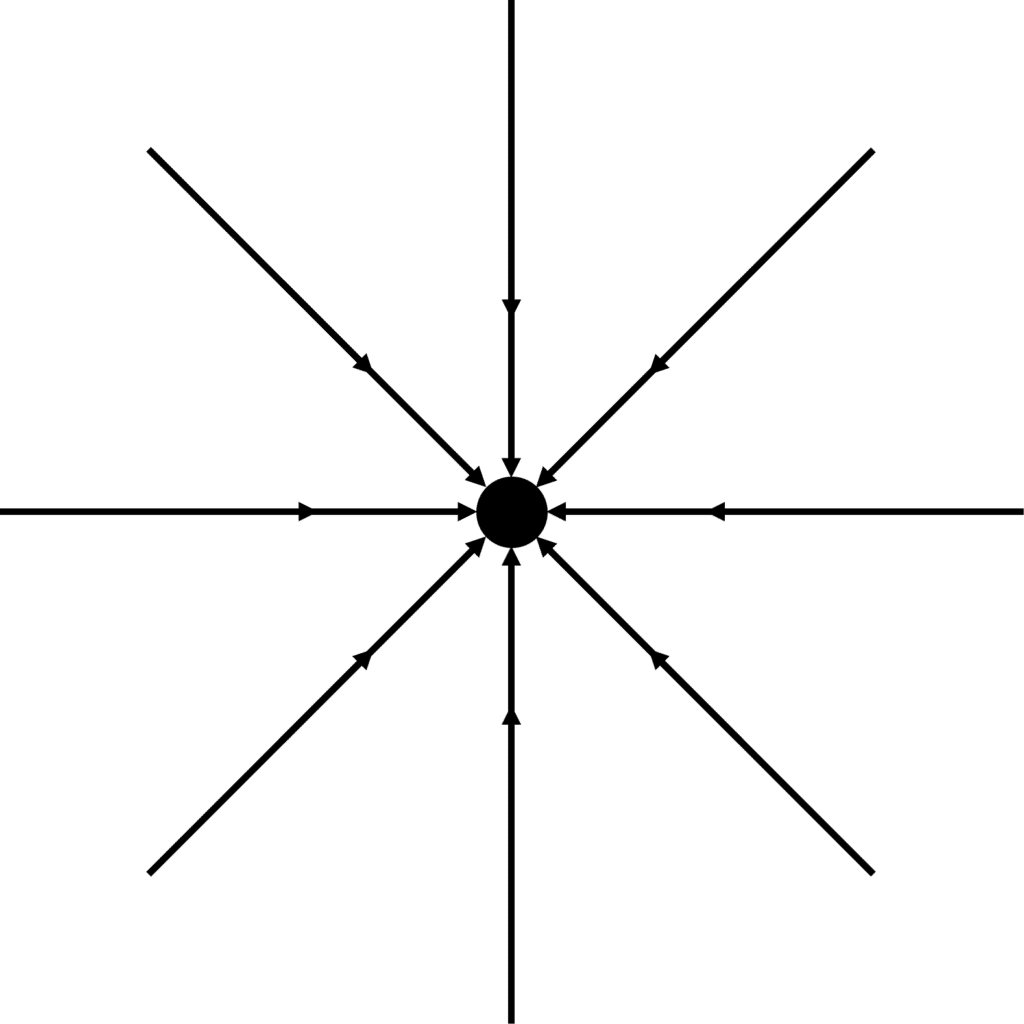

On the diagram on the right, the Earth is represented as a point mass.
Any spherical object which has its mass evenly spread like a star or a planet may be considered a point mass.
Gravitational Field Strength
Any object with a mass exerts a force of attraction in the area around it known as gravity. The greater the mass of the object, the greater the field strength produced. For most common objects we do not feel the effects of this force as their mass and field strength is tiny compared to that of the Earth.
Gravitational forces always act towards the centre of the object and can only be an attractive force.
The gravitational field strength at any point within a gravitational field is defined as the force per unit of mass exerted on a body. We need to recall that the gravitational field strength \left(g\right) on Earth is approximately 9.81 \: \text{Nkg}^{-1}, but this number varies for other planets and stars. This can be represented in the equation:
g = \dfrac{F}{m}
- g is the gravitational field strength in Newtons per kilogram \left(\text{Nkg}^{-1}\right).
- F is the force in Newtons \left(\text{N}\right).
- m is the mass in kilograms \left(\text{kg}\right).
Example: Calculate the force exerted on a 70 \: \text{kg} object on a planet with \dfrac{1}{3} of the gravitational field strength of Earth.
[2 marks]
We know that g on earth is 9.81 \: \text{Nkg}^{-1}, then g on the planet will be \dfrac{9.81}{3} = \boldsymbol{3.27 \: }\textbf{Nkg}^{-1}.
g = \dfrac{F}{m} rearranges to F = g \times m.
F = 3.27 \times 70 = \boldsymbol{230} \: \textbf{N}.
Mass and Weight
The mass of an object is determined by the amount of matter that makes the object up and is measured in kg. This does not change even if gravitational field strength does. Therefore it can be considered a constant.
However, weight is a force \left(N\right) and it is determined by gravitational field strength. Therefore, we can write the following equation based on our gravitational field strength equation:
W = m \times g
- W is weight in Newtons \left(N\right).
- m is mass in \left(\text{kg}\right).
- g is gravitational field strength in Newtons per kilogram \left(\text{Nkg}^{-1}\right).
Weight is not constant on different planets/stars. This is because weight is dependent upon the gravitational field strength of the planet/star that the object is on.
Drawing Gravitational Fields
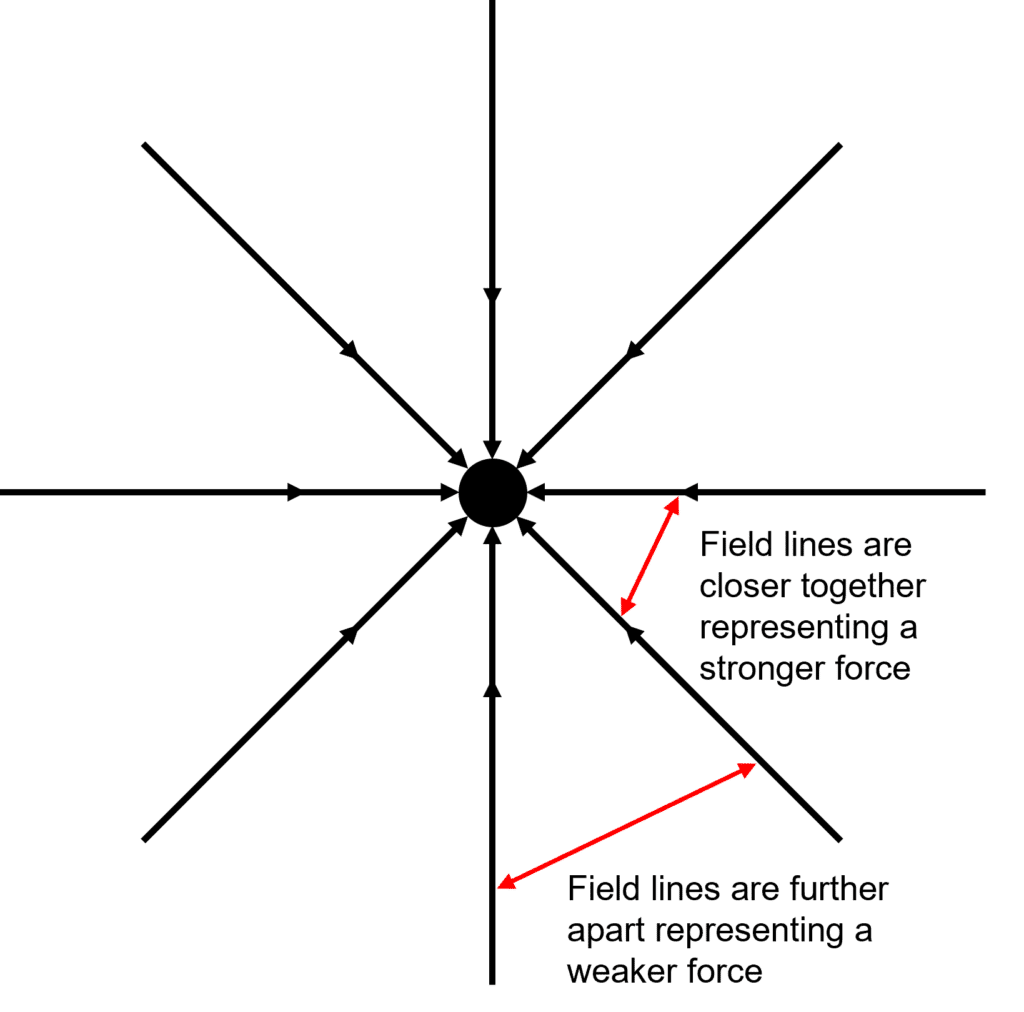

Gravitational fields are an example of a radial field.
Radial fields act towards the centre of the mass and are an attractive force. They act radially inwards towards the point mass.
For massive objects like planets or stars, we can represent the object as a point mass.
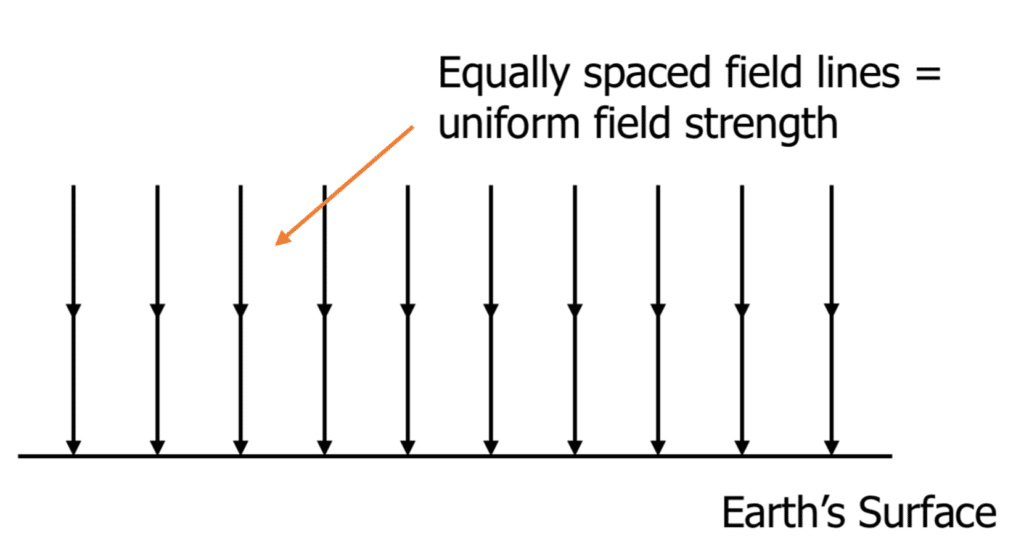

However, if we were to look at a smaller part of the surface of a planet, the curvature is so small that the surface could be considered flat.
Therefore the gravitational field strength could be represented as a uniform field.
Fields Example Questions
Question 1: What is a force field?
[1 mark]
The area around a body that will experience a non contact force.
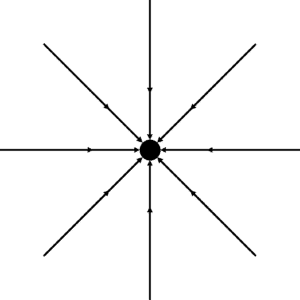
Question 2: Below is a field around a point mass. How would you expect this field to be different for another point mass with a stronger field?
[1 mark]
The field lines would be closer together at all points around the point mass.
Question 3: Define gravitational field strength.
[1 mark]
The force per unit of mass exerted on a body. It may also be defined as an equation where \boldsymbol{g= \dfrac{F}{m}}.
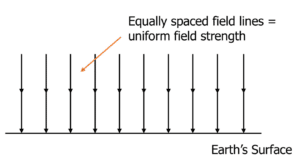
Question 4: The diagram below shows a uniform gravitational field. How would the diagram change if a change in density caused the field strength to be non-uniform?
[2 marks]
The field lines would no longer be equal distances apart. Areas where the field strength was stronger would have field lines that are closer together and where the field strength is weaker the lines would be further apart.
Question 5: Calculate the mass of a body of weight 800 \: \text{N} on a planet of gravitational field strength of 15 \: \text{Nkg}^{-1}.
[2 marks]
You May Also Like...

MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.