Newton's Law of Gravitation
Newton's Law of Gravitation Revision
Newton’s Law of Gravitation and Gravitational Potential
Sir Isaac Newton made a massive impact in our understanding of physics. One of his famous contributions to physics was the idea of gravitation. In this section we look at Newton’s law of gravitation and gravitational potential.
Newton’s Law of Gravitation
Isaac Newton aimed to calculate the force of gravity acting between two objects. For his calculations, he modelled the objects as point masses. His law of gravitation can be applied to calculate the gravitational force between two point masses (any spherical object like planets or stars).
Newton’s law of gravitation states that any object with a mass will attract another object with a mass proportionally to the product of their mass and inversely proportionally to their separation squared. Therefore:
F \propto m_1 m_2
F \propto \dfrac{1}{r^2}
This results in an equation we will discuss in the next section.
Calculating Gravitational Force Between Two Objects
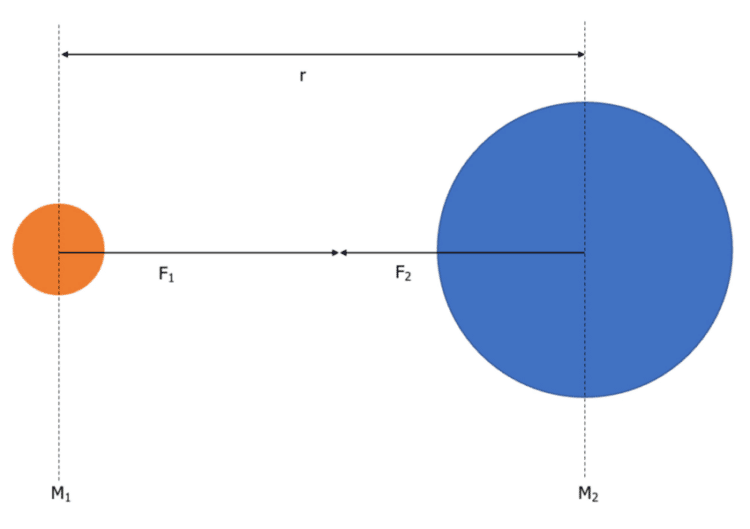
The diagram above shows two masses with a separation of r.
We can say that F_1 = F_2 = F_G. We can write the gravitational force as:
F_G = \dfrac{Gm_1m_2}{r^2}
- F_G is the gravitational force between two masses in Newtons \left(\text{N}\right).
- G is Newton’s gravitational constant, which is 6.67 \times 10^{-11} \: \text{Nm}^2 \text{kg}^{-2}.
- r is the separation of the two masses in metres \left(\text{m}\right).
- m_1 and m_2 are the masses of each object in kilograms \left(\text{kg}\right).
It is important that the separation is measured from the centre of each point mass rather than the surface.
As the force due to gravity between the two objects is inversely proportional to the separation squared, we can conclude that the force between the two objects follows the inverse square law. Therefore doubling the distance between the two objects causes the force to decrease by four times etc.
Example: A satellite is orbiting the Earth at a distance of 2500 metres above the surface of the Earth. Given the below information, calculate the force due to gravity on the satellite.
Mass of Satellite = 5000 \: \text{kg}
Mass of the Earth = 5.97 \times 10^{24} \: \text{kg}
Radius of Earth = 6.37 \times 10^6 \: \text{m}
Gravitational constant \left(G\right) = 6.67 \times 10^{-11} \text{Nm}^2 \text{kg}^{-2}
[4 marks]
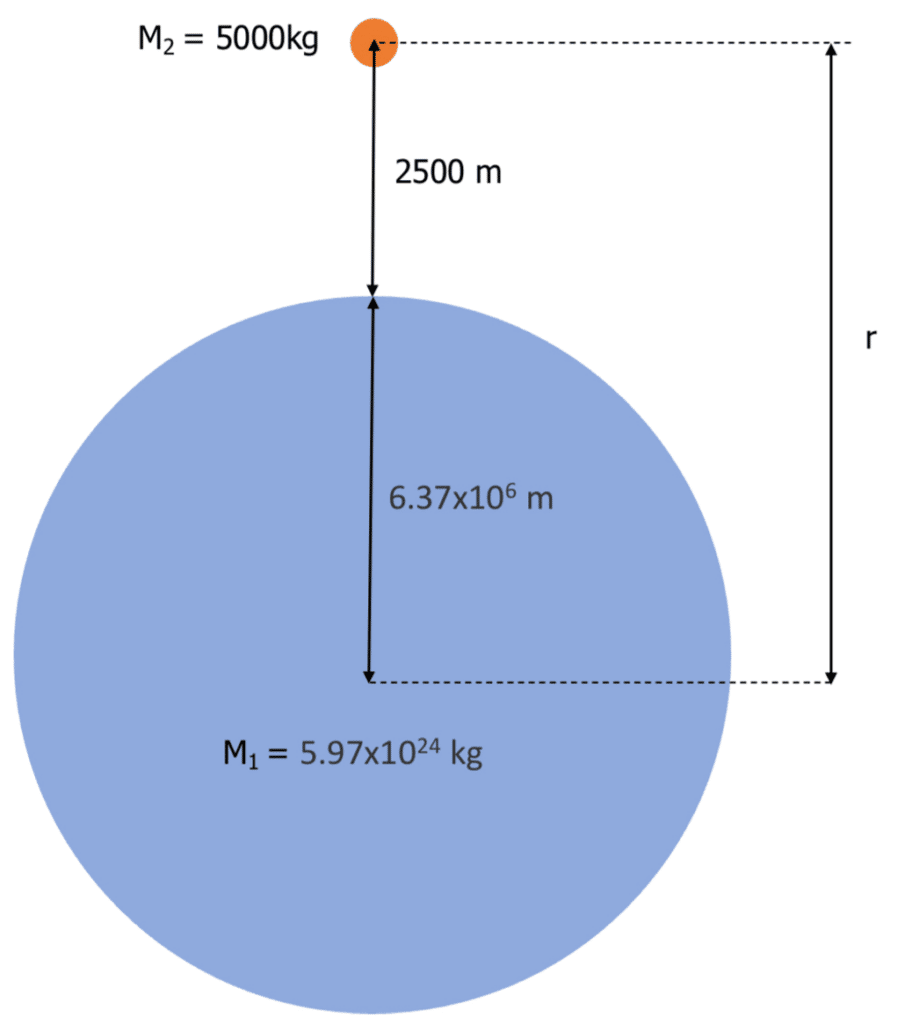

To understand this question further, draw a diagram of what we know from the question:
F_G = \dfrac{Gm_1m_2}{r^2}
F_G = \dfrac{\left(6.67 \times 10^{-11} \times 5.97 \times 10^{24} \times 5000 \right)}{\left(2500 + 6.37 \times 10^6\right)^2}
F_G =\boldsymbol{ 4.9 \times 10^4} \: \textbf{N} \: \text{or} \: \boldsymbol{49}\textbf{kN}
Gravitational Field Strength in a Radial Field
Previously we learnt how to calculate the gravitational field strength on an object. However, we also discussed that the gravitational field strength varies with distance away from the object causing the gravitational force.
To calculate the the gravitational field strength \left(g\right) at any point within a radial field, the following equation can be applied:
g = \dfrac{GM}{r^2}
- g is the gravitational field strength in Newtons per kilogram or metres per second squared \left(\text{Nkg}^{-1} \: \text{or} \: \text{ms}^{-2}\right)
- G is Newton’s gravitational constant, which is 6.67 \times 10^{-11} \: \text{Nm}^2 \text{kg}^{-2}.
- M is the mass of the body producing the field in kilograms \left(\text{kg}\right).
- r is the separation between the body causing the force and the point you are trying to calculate in metres \left(\text{m}\right).
Example: What would the mass of the moon need to be to produce a gravitational field strength at its surface the same as the Earth’s?
Radius of moon = 1.74 \times 10^6 \text{m}
Gravitational constant \left(G\right) = 6.67 \times 10^{-11} \: \text{Nm}^2\text{kg}^{-2}
Gravitational field strength at the Earth’s surface = 9.81 \: \text{Nkg}^{-1}
[3 marks]
g = \dfrac{GM}{r^2}
This rearranges to give:
M = \dfrac{gr^2}{G}
g on earth is 9.81 \: \text{Nkg}^{-1}. So we use this in our equation:
M = \dfrac{\left(9.81 \times 1.74 \times 10^6\right)}{\left(6.67 \times 10^{-11}\right)}
M = 4.45 \times 10^{23} \: \text{kg}
Therefore the moon would have to have a mass of 4.45 \times 10^{23} \: \text{kg} to produce a gravitational field of 9.81 \: \text{Nkg}^{-1} at it’s surface.
Gravitational Potential
The gravitational potential energy can be described as the amount of energy a body has due to its position within a gravitational field.
The gravitational potential \left(V\right) is another term commonly used and can be defined as the work done per unit mass when moving a mass at rest from infinity to a given point. In this definition, infinity is a point outside the gravitational field.
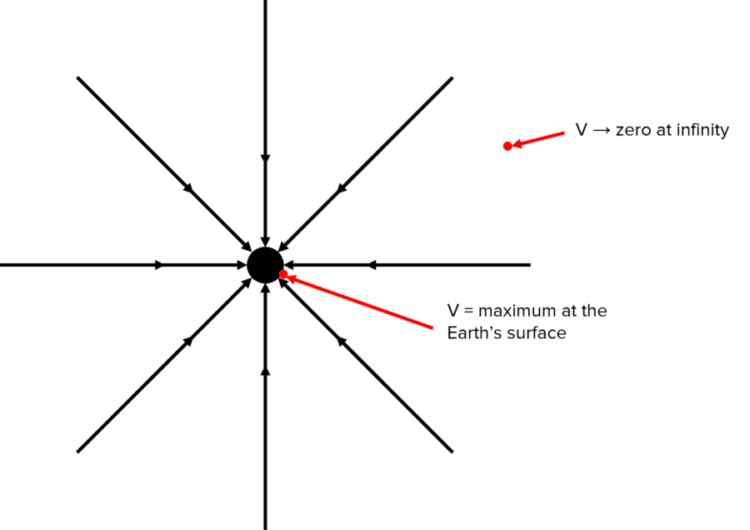
Gravitational potential is always negative as work is done against gravity as the body moves from the surface of the Earth to infinity. The gravitational potential will always be maximum at the surface and decrease to zero at infinity.
Gravitational potential can be calculated using the equation:
V = \dfrac{-GM}{r}
- V is the gravitational potential in joules per kilogram \left(\text{Jkg}^{-1}\right).
- G is Newton’s gravitational constant, which is 6.67 \times 10^{-11} \: \text{Nm}^2 \text{kg}^{-2}.
- M is the mass of the body producing the force in kilograms \left(\text{kg}\right).
- r is the separation between the body causing the force and the point in metres \left(\text{m}\right).
Example: A planet of mass 1.2 \times 10^{23} \: \text{kg} has a diameter of 5000 \: \text{km}. A large piece of rock is accelerated towards the planet and has a mass of 600 \: \text{kg}. What would the gravitational potential of the rock be at a distance of 500 \: \text{km} from the surface of the planet?
[3 marks]
r = \dfrac{5000}{2} + 500 = 3000 \: \text{km} = 3 \times 10^6 \: \text{m}
V = \dfrac{-GM}{r}
V = \dfrac{\left(-6.67 \times 10^{-11} \times 1.2 \times 10^{23}\right)}{3 \times 10^6}
V = \boldsymbol{-2.7 \times 10^6} \: \textbf{Jkg}^{-1}
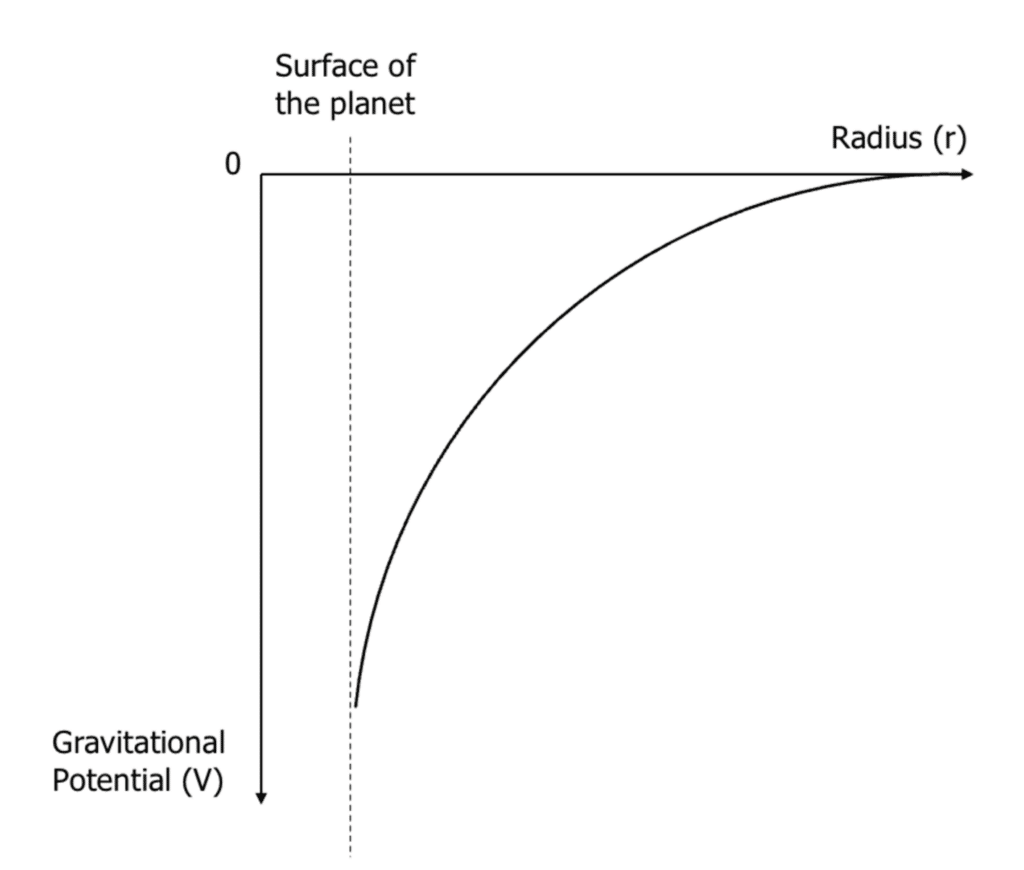

The graph represents the relationship between gravitational potential \left(V\right) and distance from the centre of the planet \left(r\right).
It shows how gravitational potential is always negative and it approaches zero at infinity.
Gravitational Potential Difference
Gravitational potential difference \left(\Delta V\right) can be used to describe the difference in gravitational potential \left(V\right) between two points within the gravitational field.
\Delta V = V_f – V_i
where V_f is the final gravitational potential and V_i is the initial gravitational potential, both in joules per kilogram \left(\text{Jkg}^{-1}\right).
Newton's Law of Gravitation Example Questions
Question 1: Describe Newton’s law of gravitation.
[2 marks]
Newton’s law of gravitation states that any object with a mass will attract another object with a mass, proportionally to the product of their mass and inversely proportionally to their separation squared.
OR
\boldsymbol{F_G = \dfrac{Gm_1m_2}{r^2}}
Question 2: A body is orbiting the Earth at a distance of 5700 \: \text{m} above the surface of the Earth. Given the below information, calculate the force due to gravity on the satellite.
Mass of Satellite = 8000 \: \text{kg}
Mass of the Earth = 5.97 \times 10^{24} \: \text{kg}
Radius of Earth = 6.37 \times 10^6 \: \text{m}
Gravitational constant \left(G\right) = 6.67 \times 10^{-11} \: \text{Nm}^2 \text{kg}^{-2}
[4 marks]
Question 3: Describe the relationship between radius and gravitational potential.
[1 mark]
As the radius increases, the gravitational potential also increases as it approaches zero.
Question 4: A planet of mass 3.9 \times 10^{23} \: \text{kg} has a diameter of 7000 \: \text{km}. A large piece of rock is accelerated towards the planet and has a mass of 1000 \: \text{kg}. What would the gravitational potential of the rock be at a distance of 200 \: \text{km} from the surface of the planet?
[3 marks]
\begin{aligned} r &= \dfrac{7000}{2} + 1000 = 4500 \: \text{km} = 4.5 \times 10^6 \: \text{m} \\ V &= \dfrac{-GM}{r} \\ V &= \dfrac{\left(-6.67 \times 10^{-11} \times 3.9 \times 10^{23}\right)}{4.5 \times 10^6} \\ V &= \boldsymbol{-5.8 \times 10^6} \: \text{Jkg}^{-1}\end{aligned}
Newton's Law of Gravitation Worksheet and Example Questions
Gravitational Field Questions
A LevelOfficial MMEYou May Also Like...

MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.