Circular Motion
Circular Motion Revision
Circular Motion
Many objects around us move in circular motion. Satellites orbiting the Earth, roundabouts and tools all move in circular motion. This unit looks at some of the calculations needed when objects are moving in circular motion.
The Mechanics of Circular Motion
An object in uniform circular motion has a constant linear velocity. However, as velocity is a vector quantity, an object in uniform circular motion is considered to be accelerating, as direction is constantly changing.
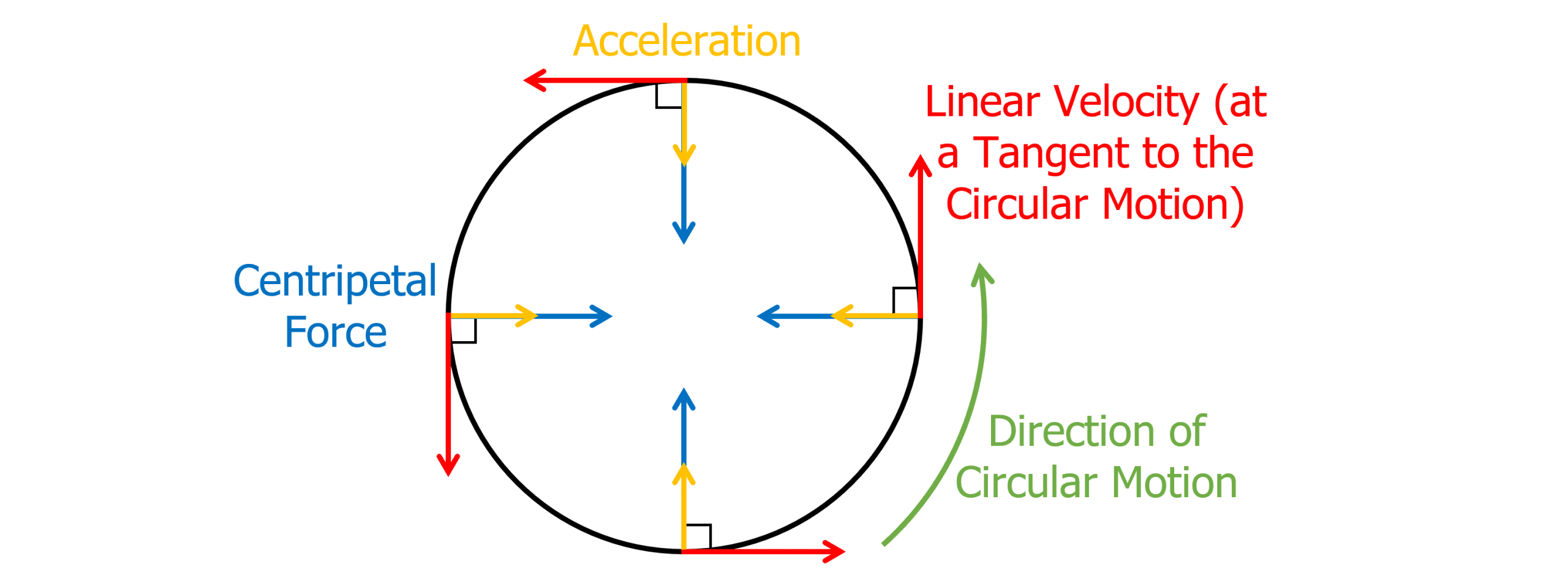
The object in uniform circular motion is kept in circular motion by a centripetal force (F) which always acts towards the centre of the circle. The centripetal force causes a centripetal acceleration (a) which also acts towards the centre of the circle.
Using Radians
Often calculations for this unit can be made using radians, instead of degrees. It is therefore important to understand what radians are and how to convert between degrees and radians.
The change in angle of an object as it rotates is known as angular displacement (\theta) and is usually stated as an angle in radians. This can be calculated using the equation:
\theta=\dfrac{l}{r}
- \theta = angular displacement in radians \text{(rad)}
- l= arc length (distance travelled around the circle) in metres \text{(m)}
- r= radius of the circle in metres \text{(m)}
Example: An object is in uniform circular motion with a radius of 2 \text{ m}. Calculate the angular displacement if the object moves 3 \text{ m} around its circular path.
[2 marks]
\theta = \dfrac{\textcolor{f95d27}{3}}{\textcolor{10a6f3}{2}} = 1.5 \text{ rad}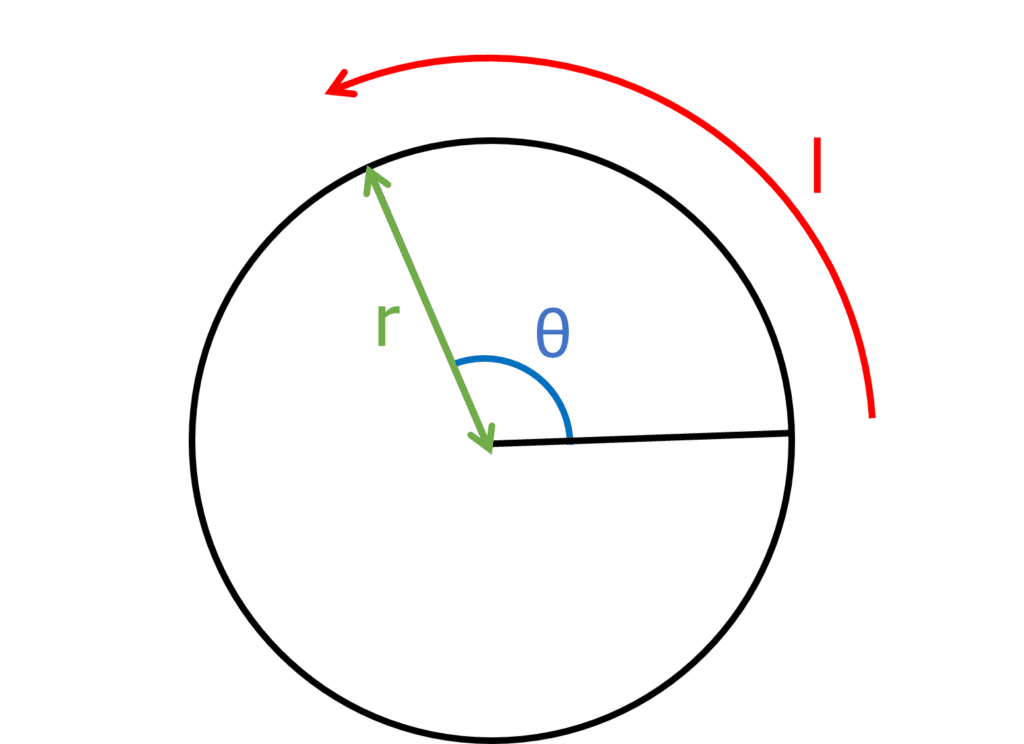

To convert between degrees and radians, the following conversions can be used:
\text{angle in} \degree \times \dfrac{\pi}{180}=\text{angle in rad}
Or:
\text{angle in rad} \times \dfrac{180}{\pi} = \text{angle in} \degree
Example: An object spins in uniform circular motion with a radius of 0.5 \text{ m}. Calculate the angular displacement in degrees if the object moves 0.25 \text{ m} around its circular path.
[3 marks]
\theta = \dfrac{\textcolor{ffad05}{0.25}}{\textcolor{00d865}{0.5}} = \bold{0.5} \textbf{ rad} \\ \begin{aligned} \text{angle in radians} \times \dfrac{180}{\pi} &= \text{angle in }\degree \\ &= 0.5 \times \dfrac{180}{\pi} \\ &= \bold{28.6 \degree}\end{aligned}
Angular Velocity
The rate of change of angular displacement is known as the angular velocity (\omega). The units for angular velocity are radians per second \text{(rads}^{-1}\text{)} making it important to remember the equations above for converting to radians.
To calculate angular velocity, the following equation is used:
\omega = \dfrac{\Delta \theta}{\Delta t}
- \omega= the angular velocity in radians per second \text{(rads}^{-1}\text{)}
- \Delta \theta= the angular displacement in radians \text{(rad)}
- \Delta t= time in seconds \text{(s)}
For an object completing a full circle of circular motion in time period, the angular velocity can be calculated using the equation:
\omega = \dfrac{2\pi}{T}= 2\pi f
- \omega= the angular velocity in radians per second \text{(rads}^{-1}\text{)}
- T= the time period in seconds \text{(s)}
- f= the frequency in hertz \text{(Hz)}
Example: A fairground ride spins children on a swing in circular motion. If the children complete one full circle in 5 \text{ s}, what is their angular velocity?
[2 marks]
\begin{aligned} \bold{\omega} &= \bold{\dfrac{2\pi}{T}} \\ &= \dfrac{2\pi}{\textcolor{aa57ff}{5}} \\ &= \bold{1.3} \textbf{ rads} \bold{^{-1}} \end{aligned}
Centripetal Acceleration
As previously seen, the centripetal acceleration (a) is the acceleration towards the centre of the circle when an object is spinning in uniform circular motion. Centripetal acceleration can be calculated using:
a=\dfrac{v^2}{r}
- a= centripetal acceleration in radians per second squared \text{(rads}^{-2}\text{)}
- v= linear speed in metres per second (\text{ms}^{-1})
- r= the radius in metres \text{(m)}
And as v=r\omega, substituting into the above equation gives:
a=r\omega ^2
- a= centripetal acceleration in radians per second squared \text{(rads}^{-2}\text{)}
- r= the radius in metres \text{(m)}
- \omega= the angular velocity in radians per second \text{(rads}^{-1}\text{)}
Example: A fairground ride spins children on a swing in circular motion at a radius of 4 \text{ m}. If the children complete one full circle in 3 \text{ s}, what is their angular velocity?
[3 marks]
\begin{aligned} \omega &= \dfrac{2\pi}{T} \\ &= \dfrac{2\pi}{\textcolor{f21cc2}{3}} \\ &= \bold{2.095} \textbf{ rads} \bold{^{-1}} \\ \bold{a} &= \bold{r \omega^2} \\ &= \textcolor{f95d27}{4} \times 2.095^2 \\ &= \bold{18} \textbf{ ms} \bold{^{-2}} \end{aligned}
Centripetal Force
The centripetal force is the resultant force in Newtons \text{(N)} acting towards the centre of a circle, keeping the object moving in circular motion.
As F=ma and a=\dfrac{v^2}{r}:
F=\dfrac{mv^2}{r}= m\omega^2r
As objects stay in circular motion for different reasons, the centripetal force may exist as tension in a string, friction of car tyres going around a corner, or gravity acting on an object in orbit.
Example: A car of mass 1200 \text{ kg} is travelling around a circular racing track of radius 200 \text{ m}. The car is moving at a constant speed of 40 \text{ ms}^{-1}. What is the centripetal force needed to keep the car in circular motion?
[2 marks]
\begin{aligned} \bold{F} &= \bold{\dfrac{mv^2}{r}} \\ &= \dfrac{\textcolor{10a6f3}{1200} \times \textcolor{f21cc2}{40}^2}{\textcolor{00d865}{200}} \\ &= \bold{9600} \textbf{ N}\end{aligned}
Circular Motion Example Questions
Question 1: Why is an object in uniform circular motion considered to be accelerating, even if its speed does not change?
[2 marks]
Velocity is a vector quantity meaning it has a magnitude and direction. As the direction is constantly changing, the velocity is constantly changing. Therefore the object is accelerating as acceleration is change in velocity per unit of time.
Question 2: A child’s roundabout moves in circular motion. If the children complete one full circle in 2 \text{ s}, what is their angular velocity?
[2 marks]
Question 3: A swingball game in circular motion at a radius of 0.8 \text{ m}. If the ball completes one full circle in 1.2 \text{ s}, what is the ball’s angular acceleration?
[3 marks]
Question 4: A go cart of mass 300 \text{ kg} is travelling around a circular racing track of radius 150 \text{ m}. The go cart is moving at a constant speed of 30 \text{ ms}^{-1}. What is the centripetal force needed to keep the car in circular motion?
[2 marks]
Circular Motion Worksheet and Example Questions
Circular Motion Questions
A LevelOfficial MMEYou May Also Like...

MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.