Electromotive Force and Internal Resistance

A LevelAS LevelAQA

Electromotive Force and Internal Resistance Revision

Electromotive Force and Internal Resistance

It is the role of the power source to supply the circuit and its components with energy. If the power source is a battery or a cell, chemical energy is converted to electrical energy. However, this process is not always 100 percent efficient. In this section we look into the Electromotive Force (EMF) and internal resistance of batteries and cells.

Electromotive Force

The electromotive force (EMF) of a cell is the amount of energy transferred per coulomb of charge. This is given in the equation:

$\varepsilon = \dfrac{E}{Q}$

$\varepsilon=$ the EMF of the cell in volts $\text{(V)}$
$E=$ the energy supplied in joules $\text{(J)}$
$Q=$ charge in coulombs $\text{(C)}$

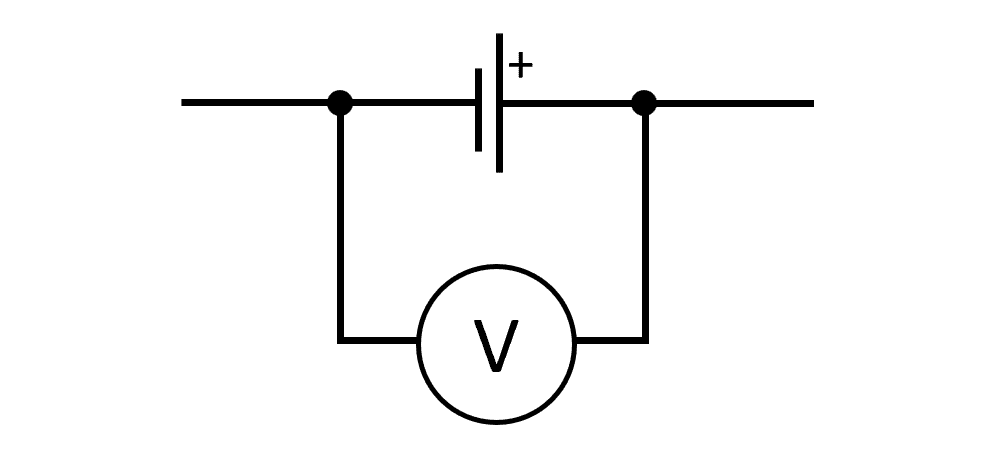
EMF can be directly measured in a circuit by placing a voltmeter in parallel across the terminals of the battery whilst not connected to a circuit.

Terminal pd is the potential difference measured across the terminals of the power source when the circuit is under load. It is the maximum potential difference the circuit actually receives.

The EMF will always be greater than the terminal pd whilst connected to the circuit as the cell has to overcome its own internal resistance. The difference between EMF and terminal pd is known as the lost volts $(v)$ .

As $V=IR$ for the terminal pd, we can write a second equation for the lost volts caused by the internal resistance where:

$v=Ir$

$v=$ lost volts in volts $\text{(V)}$
$I=$ current in amps $\text{(A)}$
$r=$ internal resistance in ohms $(\Omega)$

Combining these two equations gives us a third equation:

$\varepsilon = IR+Ir = I(R+r)$

$\varepsilon=$ EMF in volts $\text{(V)}$
$I=$ current in amps $\text{(A)}$
$R=$ total resistance in ohms $(\Omega)$
$r=$ internal resistance in ohms $(\Omega)$

Internal Resistance

The internal resistance $(r)$ is the resistance caused by the materials inside of the battery. As with conventional resistance in wires and cell components, the internal resistance of the battery causes it to warm up when in use. The thermal energy that is dissipated comes from the lost volts $(v)$ due to the internal resistance inside the battery.

In most questions, you are told to consider internal resistance to be negligible and therefore, ignore its effects. However, when asked a question about EMF and internal resistance, it is important to ensure you consider their effects.

Example: A circuit with a terminal pd of $1.5 \text{ V}$ is powered by a battery with internal resistance $1.3 \text{ k}\Omega$ . The current in the circuit is $0.6 \text{ mA}$ . Calculate the EMF.

[3 marks]

$\bold{\varepsilon = IR+Ir}$

As $V=IR$ we can substitute $V$ into the equation to make:

$\begin{aligned} \bold{\varepsilon}&=\bold{V+Ir} \\ &= \textcolor{00bfa8}{1.5} + (\textcolor{00d865}{0.6 \times 10^{-3}} \times \textcolor{10a6f3}{1.3 \times 10^3}) \\&= \bold{2.28} \textbf{ V} \end{aligned}$ .

Required Practical 6

Investigating the relationship between internal resistance and emf.

Doing the experiment:

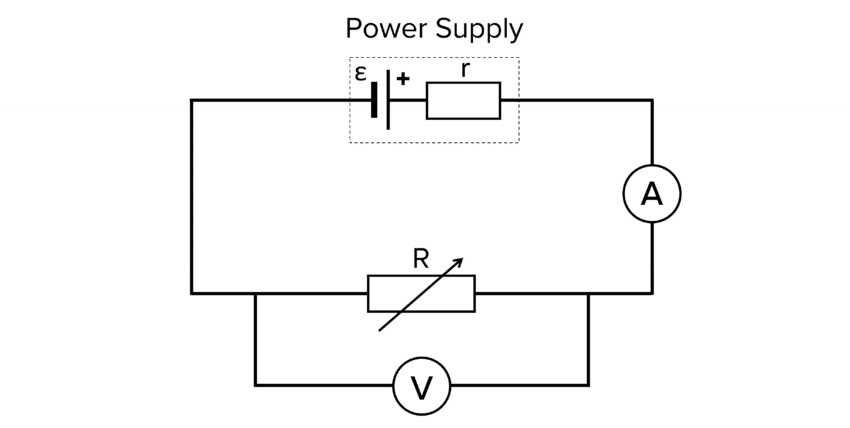
Set up the circuit as shown in the diagram above.
With one of the wires disconnected from the circuit, record the reading of $V$ on the voltmeter.
Set the variable resistor to its maximum resistance.
Switch on the power supply and reconnect the wire and record a pair of values for $V$ and $I$ , then switch off the power supply.
Repeat for $10$ values of resistance over the whole range of the variable resistor and repeat $3$ times for each resistance. This should give $10$ pairs of readings for $V$ and $I$ .

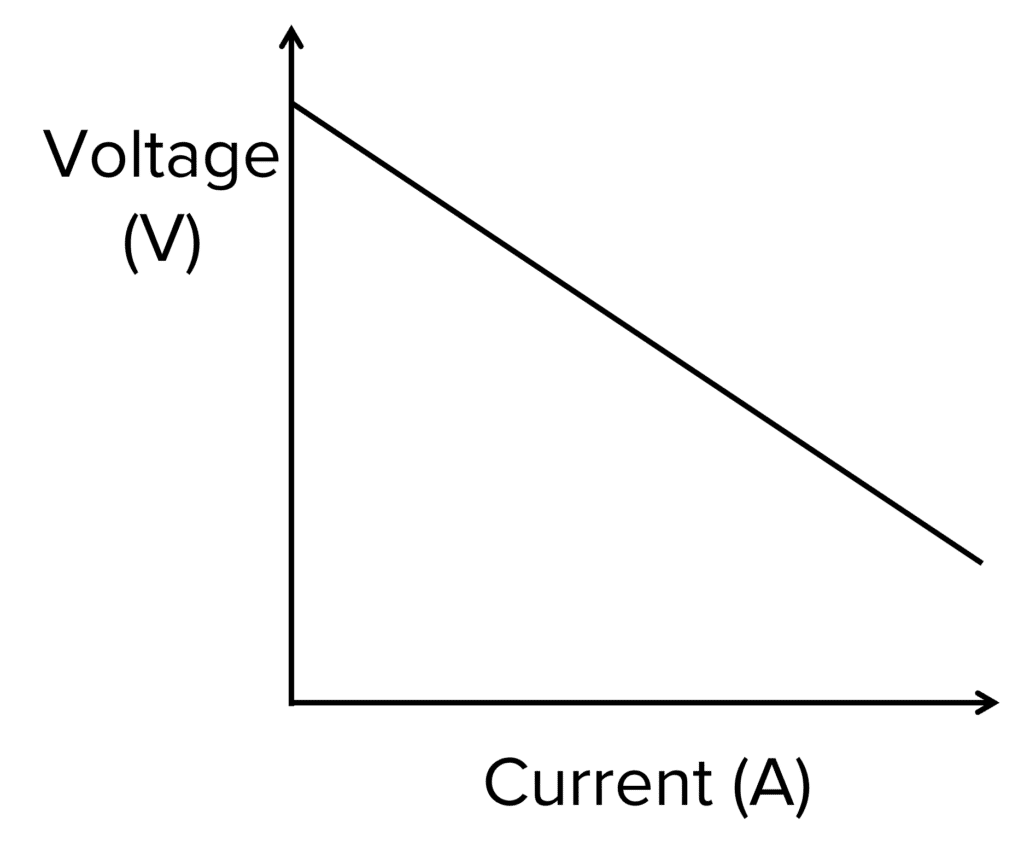
Analysis of Results:

To best analyse the results, a graph of $V$ against $I$ can be plotted which should look similar to the one on the right hand side.

In the graph, the y-intercept represents the emf whilst the gradient represents the negative of the internal resistance.

Electromotive Force and Internal Resistance Example Questions

Question 1: In the circuit below, the voltmeter shows a reading of $12 \text{ V}$ . However, when the switch is closed, the reading changes to $11 \text{ V}$ . Explain why.

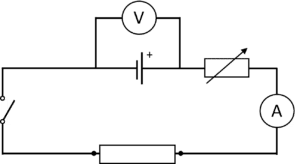[3 marks]

When the switch is open, the voltmeter is reading the EMF of the cell to be $\bold{12} \textbf{ V}$ . This is the maximum voltage the cell is capable of producing when unloaded. However, when the circuit is completed by closing the switch, the cell becomes under load. The cell has some internal resistance so some voltage is lost, known as lost volts. This is due to the cell overcoming the internal resistance of the material inside.

Save your answers with

Gold Standard Education

Question 2: A student measures the voltage of a battery in a circuit by placing a voltmeter in parallel across the terminals of a battery. They find the voltage to be $22 \text{ V}$ when the switch in the circuit is open and $20.5 \text{ V}$ when the switch is closed. Calculate the lost volts and suggest where this energy has gone.

[2 marks]

22 - 20.5 = \bold{1.5} \textbf{ V}

The energy from the lost volts will heat up the battery and dissipate into the surroundings.

Save your answers with

Gold Standard Education

Question 3: A circuit with a terminal pd of $12.5 \text{ V}$ is powered by a battery with internal resistance $2 \text{ k}\Omega$ . The current in the circuit is $2.5 \text{ mA}$ . Calculate the EMF.

[2 marks]