Simple Harmonic Motion
Simple Harmonic Motion Revision
Simple Harmonic Motion
In this section we begin looking at objects in simple harmonic motion (SHM). Examples of SHM can be seen around us from pendulums in clocks to a swing moving backwards and forwards.
SHM
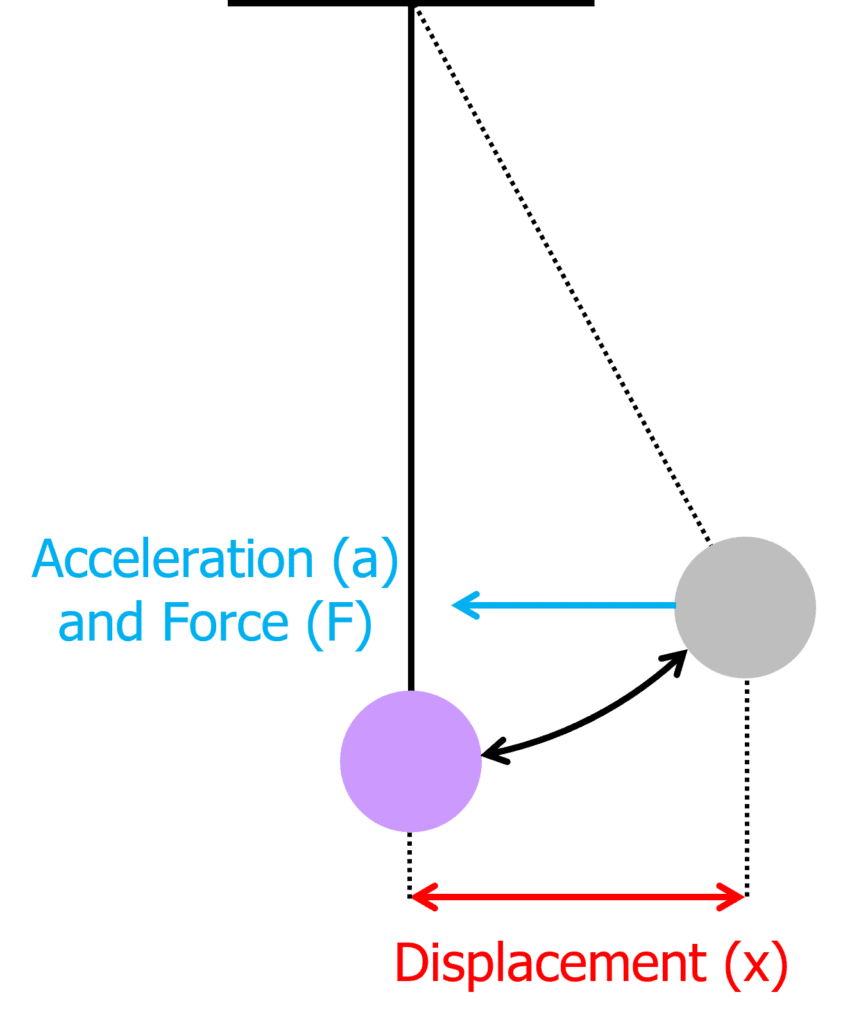

An oscillator is considered to be in simple harmonic motion (SHM) if the acceleration is proportional and opposite in direction to the displacement of the oscillator.
The acceleration of the oscillator always acts in the same direction as the restoring force. This is the force that brings the oscillator back towards the equilibrium position. The acceleration can be calculated using the equation:
a=-\omega^2 x
- a= acceleration in metres per second squared \text{(ms}^{-2}\text{)}
- \omega= angular frequency in radians per second (\text{rads}^{-1})
- x= the displacement in metres \text{(m)}
The equation shows that the maximum acceleration occurs when the displacement is maximum.
Example: A simple harmonic oscillator has a time period of 2 \text{ s} when its maximum displacement is 0.05 \text{ m}. Calculate the maximum acceleration.
[3 marks]
\bold{a= -\omega^2 x} and \bold{\omega = \dfrac{2\pi}{T}}. By substitution:
\begin{aligned} a &= -\dfrac{4\pi^2}{T^2}x \\ &= -\dfrac{4\pi^2}{\textcolor{10a6f3}{2}^2} \times \textcolor{00d865}{0.05} \\ &= \bold{-0.5} \textbf{ms}\bold{^{-2}} \end{aligned}
The displacement is directly proportional to the negative acceleration of the simple harmonic oscillator. Plotting a displacement-acceleration graph forms a straight line through the origin where the gradient is equal to \omega^2.
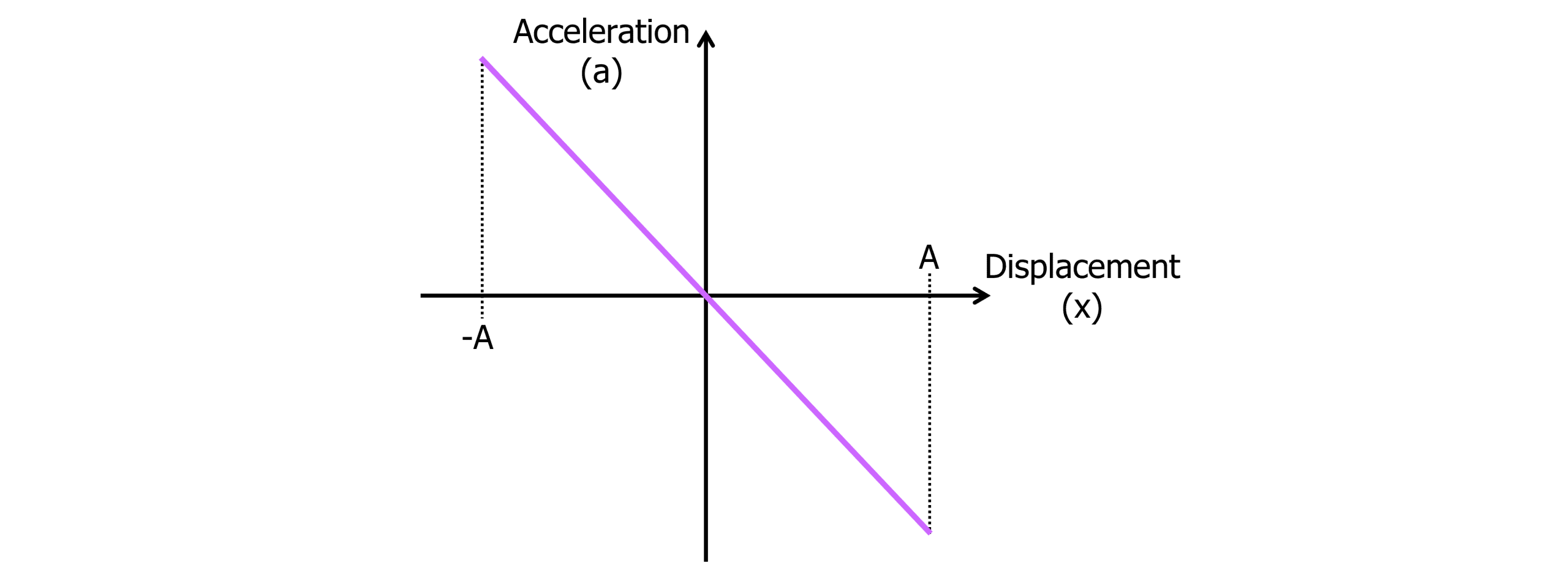
From the graph we can see the points of maximum displacement at either end. These are known as the amplitude of the simple harmonic oscillator (A). The displacement (x) at any given point can be found using the equation:
x=ACos(\omega t)
- x= the displacement in metres \text{(m)}
- A= the amplitude in metres \text{(m)}
- \omega= the angular frequency in radians per second \text{(rads}^{-1}\text{)}
- t= the time in seconds \text{(s)}
We can also calculate the speed at any given point of the simple harmonic oscillator. The speed of the oscillator would be at a minimum at its positive and negative amplitudes and at a maximum as it passes the equilibrium where x=0.
v=\pm \sqrt{A^2-x^2}
- v= the velocity in metres per second \text{(ms}^{-1}\text{)}
- A= the amplitude in metres \text{(m)}
- x= the displacement in metres \text{(m)}
Example: A simple pendulum oscillates with simple harmonic motion with an amplitude of 0.3 \text{ m}. The frequency of the oscillations is 5 \text{ Hz}. Calculate the speed of the pendulum at a position of 0.1 \text{ m} from the equilibrium position.
[3 marks]
\bold{v= \pm \omega \sqrt{A^2-x^2}} and \bold{\omega = 2 \pi f}. So by substitution:
\begin{aligned} v &= \pm 2\pi f \sqrt{A^2-x^2} \\ &= \pm 2\times \pi \times \textcolor{00d865}{5} \times \sqrt{\textcolor{ffad05}{0.3}^2-\textcolor{10a6f3}{0.1}^2} \\ &= \bold{\pm 8.9}\textbf{ ms}\bold{^{-1}} \end{aligned}
SHM Graphs
Provided a simple harmonic oscillator is undamped, we should expect to see graphs similar to the ones below for any object on simple harmonic motion.
Displacement-time graph:
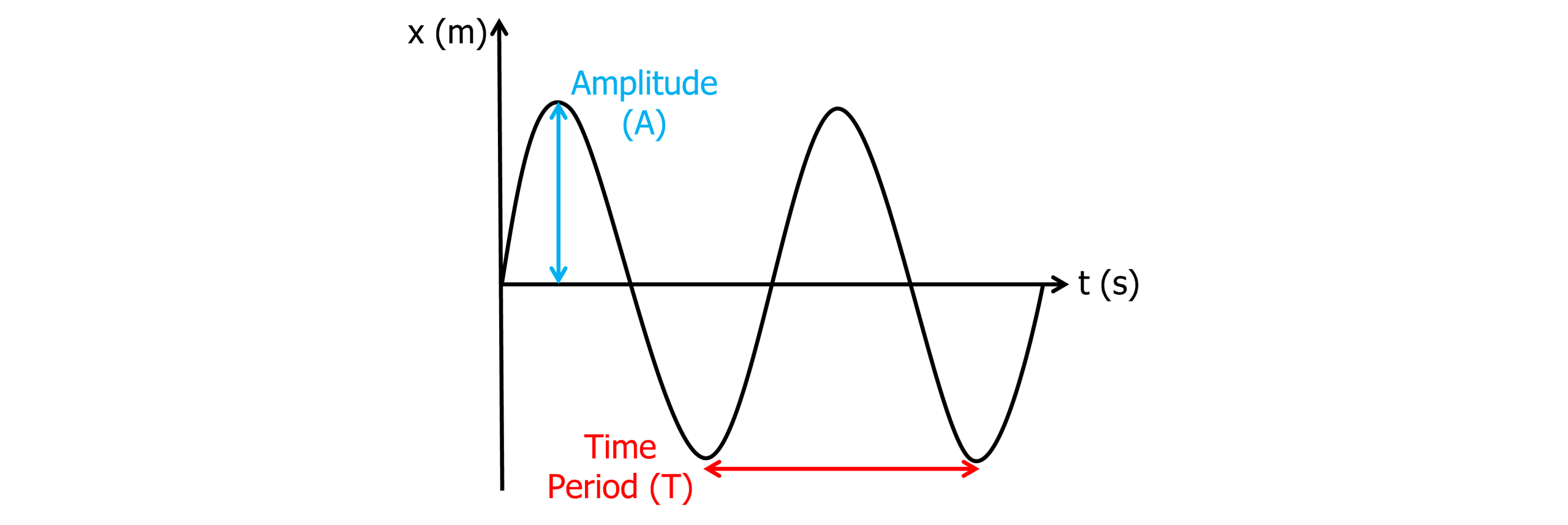
The x-t graph above is a simple sinusoidal graph. The amplitude (maximum displacement) always stays the same as there is no energy lost or gained during oscillations. Calculating the gradient at any point of the displacement-time graph gives the velocity.
Velocity-time graph:
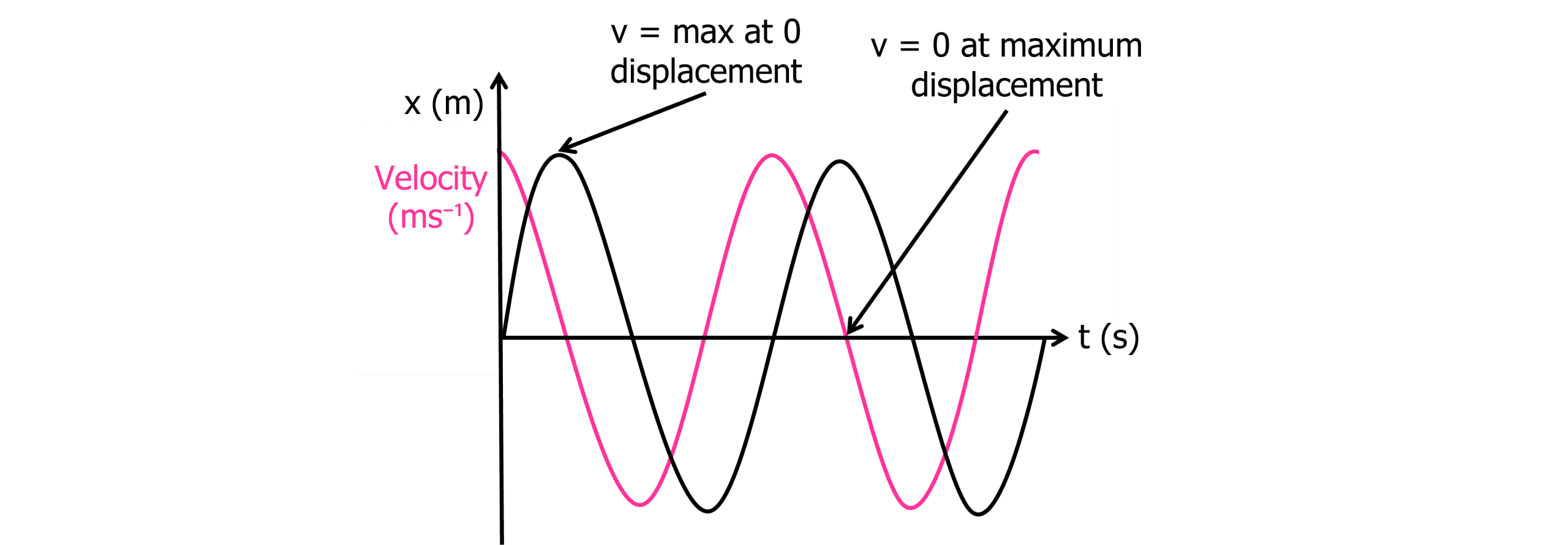
The v-t graph above is a simple cosine graph. When displacement is zero from the previous graph, the velocity is maximum. When the oscillator is at its maximum displacement, the velocity is zero. Again, as no energy is gained or lost, the maximum velocity with each oscillation remains the same. Calculating the gradient at any point on the velocity-time graph gives acceleration.
Acceleration-time graph:
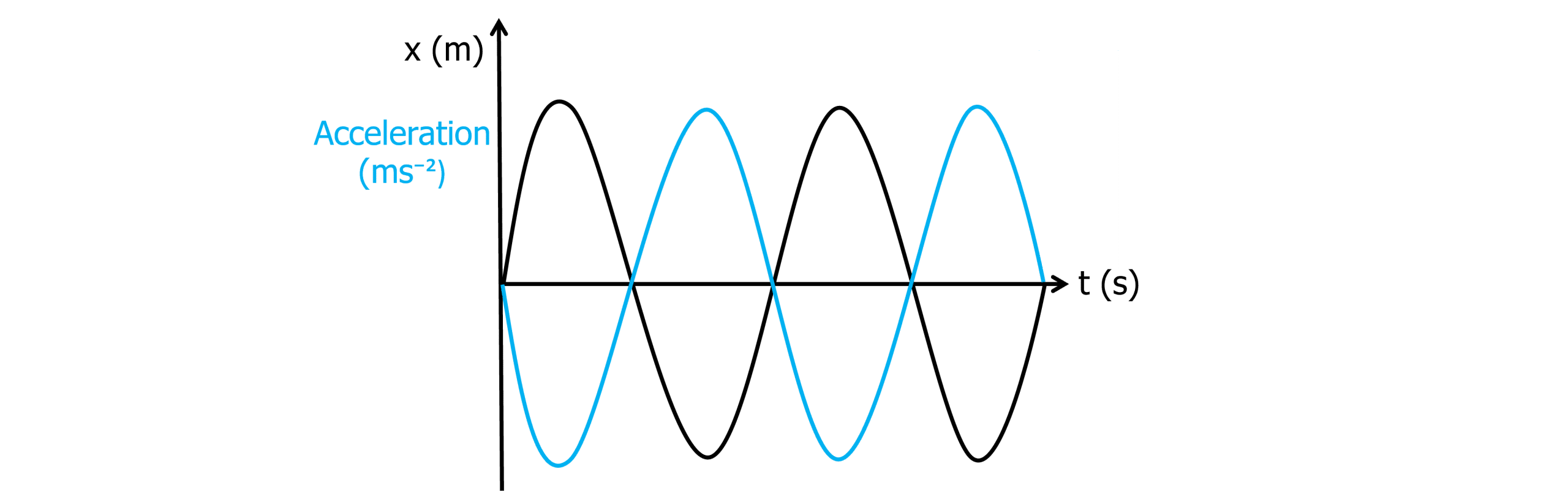
Calculating the maximum velocity of a simple harmonic oscillator can be done using a simpler equation than that learnt previously. As maximum velocity occurs when displacement (x) is zero, the equation can be simplified:
\begin{aligned} v &= \pm \omega \sqrt{A^2-x^2} \\ &= \pm \omega \sqrt{A^2+0^2} \\ &= \pm \omega \sqrt{A^2} \end{aligned}
v_{\text{max}}=\omega A
Calculating maximum acceleration can also be calculated, using the displacement at its maximum. Maximum displacement is known as the amplitude. Therefore the equation changes to:
a_{\text{max}}=\omega ^2 A
Mass-spring Systems
A mass and a spring can form a system which moves in simple harmonic motion (SHM). If a mass is pulled to maximum displacement on a spring, a restoring force will return the mass to the equilibrium position.
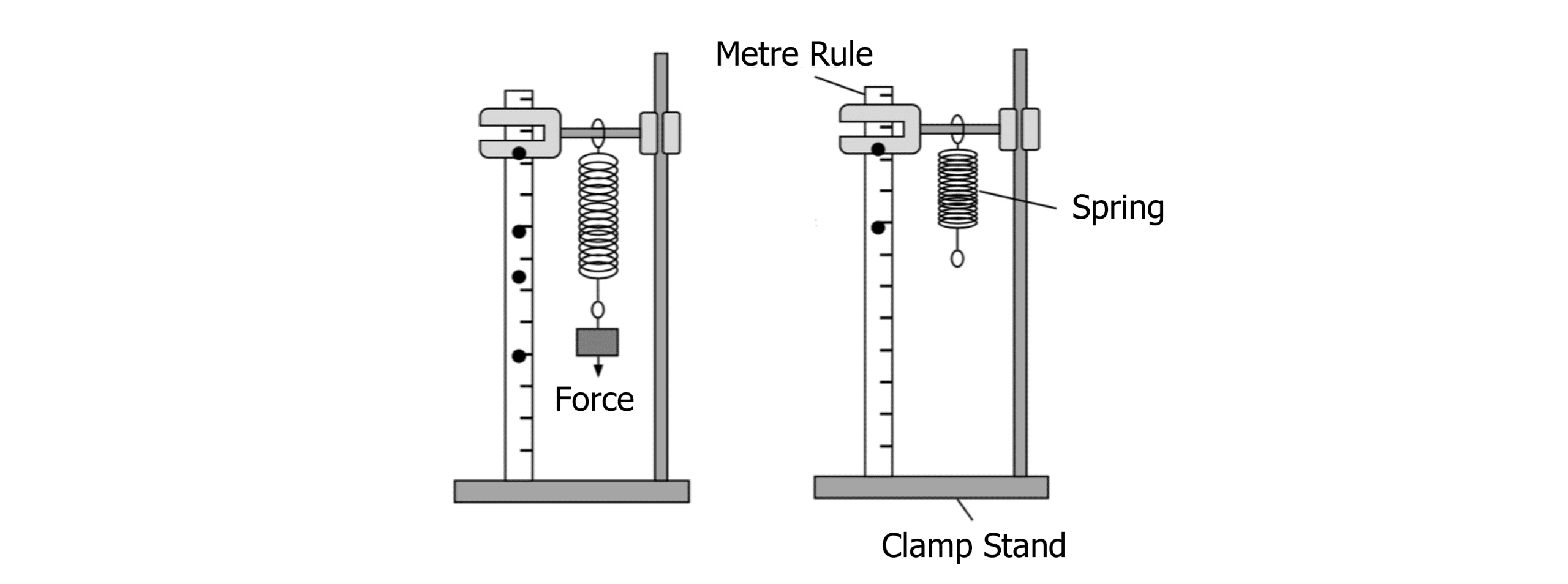
The time period of the mass-spring system can be calculated using the equation:
T=2\pi \sqrt{\dfrac{m}{k}}
- T= the time period in seconds \text{(s)}
- m= the mass in kilograms \text{(kg)}
- k= the spring constant in newtons per metre \text{Nm}^{-1}
The equation shows that the time period is proportional to mass and therefore, the greater the mass the greater the time period. It also shows an inversely proportional relationship between time period and spring constant.
Example: A spring with a spring constant of 2.2 \text{ Nm}^{-1} is extended by a mass of 5 \text{ kg}. The spring is stretched until it moves into simple harmonic motion. Calculate the time period of the oscillation.
[2 marks]
\begin{aligned} \bold{T} &= \bold{2\pi \sqrt{\dfrac{m}{k}}} \\ &= 2\pi \times \sqrt{\dfrac{\textcolor{f95d27}{5}}{\textcolor{aa57ff}{2.2}}} \\ &= \bold{9.5} \textbf{ s} \end{aligned}
Simple Pendulums
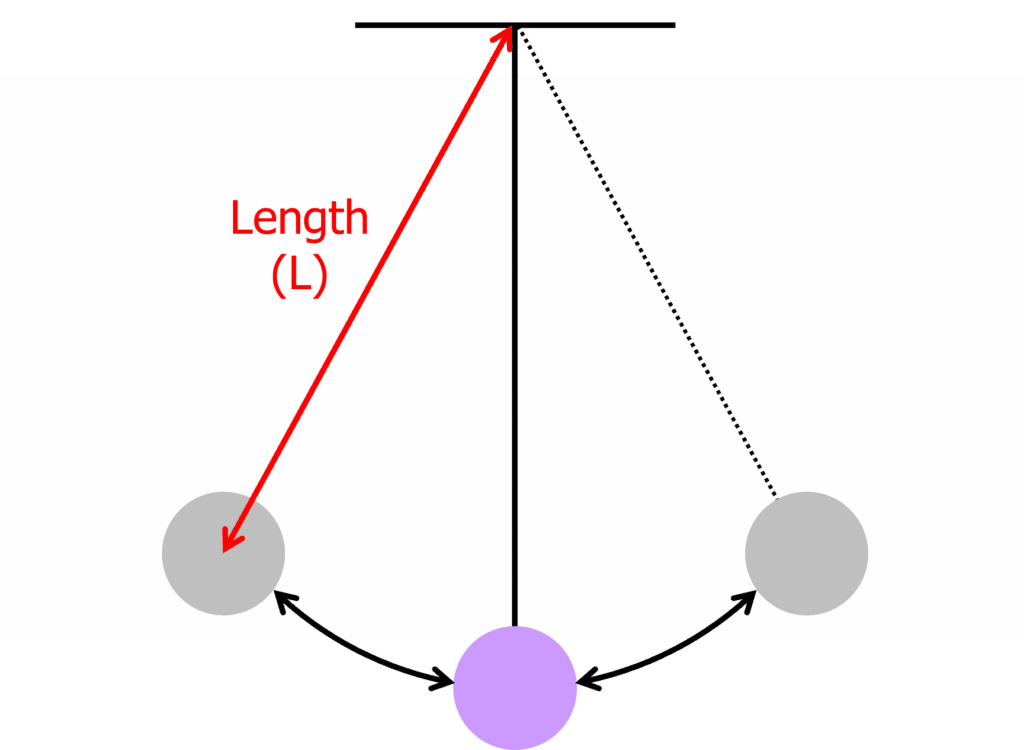

A mass and a string can form a pendulum system which moves in simple harmonic motion (SHM). If a mass is pulled to maximum displacement on a string, a restoring force will return the mass to the equilibrium position. The restoring force is the force responsible for bringing the oscillating object back to the equilibrium position.
The time period of the pendulum can be calculated using the equation:
T=2\pi\sqrt{\dfrac{L}{g}}
- T= the time period in seconds \text{(s)}
- L= the length of the string in metres \text{(m)}
- g= the gravitational field strength in newtons per kilogram \text{(Nkg}^{-1}\text{)}
g is used in the equation above as this represents the restoring force. The equation shows that the time period is proportional to length and therefore, the longer the string the greater the time period.
Example: Calculate the time period of a pendulum of length 0.5 \text{ m} on Earth.
[2 marks]
\begin{aligned} \bold{T} &= \bold{2\pi \sqrt{\dfrac{L}{g}}} \\ &= 2\pi \times \sqrt{\dfrac{\textcolor{00d865}{0.5}}{9.81}} \\ &= \bold{1.42} \textbf{ s} \end{aligned}
Required Practical 7
Calculating the spring constant of a mass-spring system.
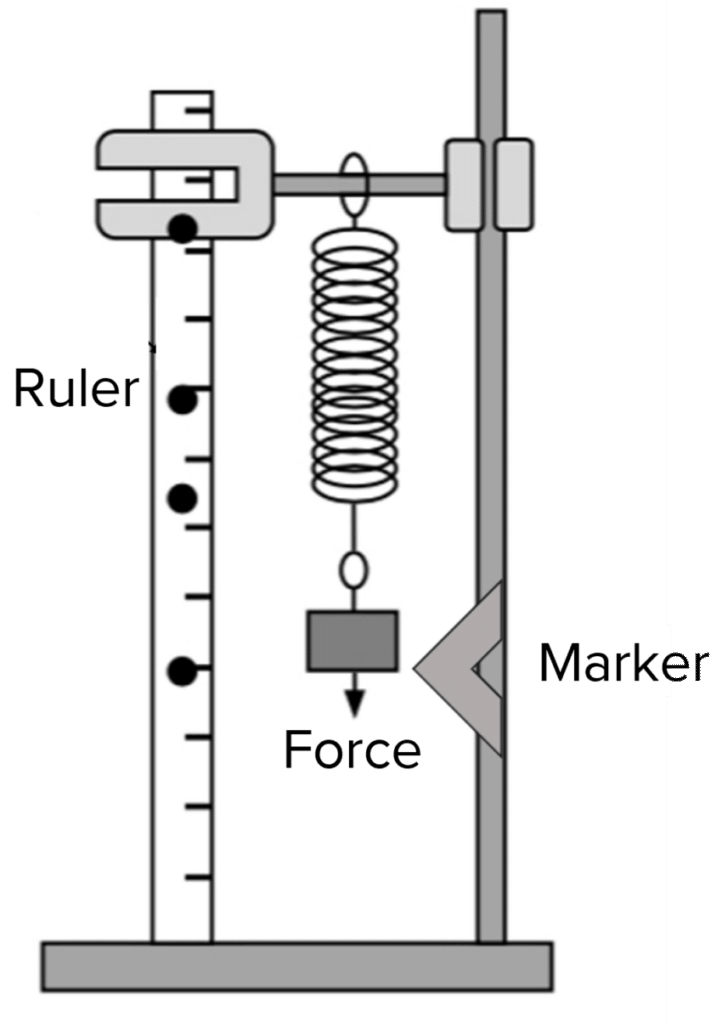

Doing the experiment:
- Set up the equipment as shown in the diagram.
- Begin with zero mass on the mass hanger. This will give us a reading with the mass set to the mass of the mass hanger.
- Pull the mass hanger down 5 \text{ cm} ensuring it passes the marker.
- Release the mass hanger and start the stopwatch when it passes the marker the first time. The mass will oscillate vertically.
- Stop the stopwatch after it passes the marker 10 times. Divide this time by 10 to get the time period (T) of the oscillations.
- Add 50 \text{ g} to the mass hanger and repeat the above steps.
- Continue this until you have 10 sets of results ranging in mass.
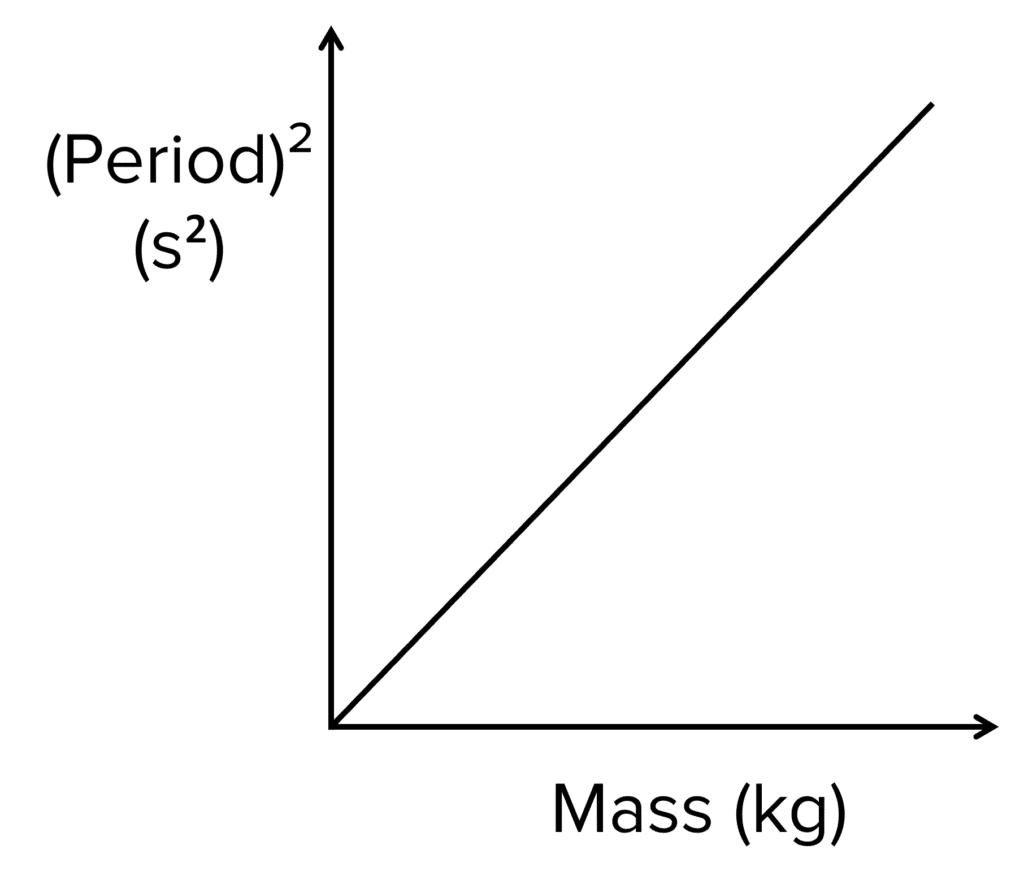
Analysing the Results:
Plot a graph of T^2 against m. You should get a graph that looks similar to the graph on the right hand side (a direct proportionality).
As the equation T = 2 \pi \sqrt{\dfrac{m}{k}} can be rearranged to give T^2 = 4 \pi ^2 \dfrac{m}{k}, the gradient of the graph represents \dfrac{4 \pi ^2}{k}.
Therefore k = \dfrac{4 \pi ^2}{\text{gradient}} where k is the spring constant of the spring.
Simple Harmonic Motion Example Questions
Question 1: Describe how you would calculate the velocity of a simple harmonic oscillator from a displacement-time graph when the graph forms a curve.
[2 marks]
The gradient of a displacement-time graph gives us the velocity. As the graph is a curved line, you would need to use a tangent to the curve then find the gradient of the tangent.
Question 2: A spring with a spring constant of 5.1 \text{ Nm} ^{-1} is extended by a mass of 4 \text{ kg}. The spring is stretched until it moves into simple harmonic motion. Calculate the time period of the oscillation.
[2 marks]
Question 3: Calculate the frequency of a pendulum of length 1.2 \text{ m} on a planet with gravitational field strength of \dfrac{1}{5} of Earth.
[3 marks]
You May Also Like...

MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.