Coulomb's Law

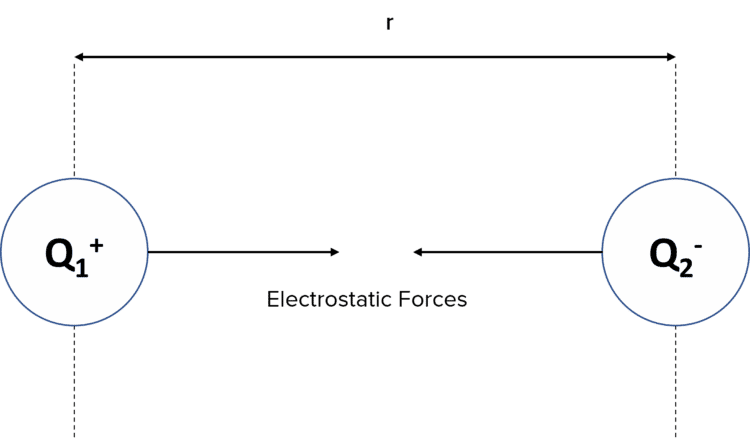
Coulomb’s Law describes how two charged particles interact with each other if they are within the electric field of one another. It states that the electrostatic force is proportional to the product of the two charges and inversely proportional to the square of the distance between the charges. We consider the charge to be at the centre of a charged sphere.

E \propto Q_1 Q_1 and E \propto \dfrac{1}{r^2}

This is represented in the equation for Coulomb’s Law:

F = \dfrac{Q_1 Q_2}{4 \pi \epsilon_0 r^2}

• F is the force between the two charges in Newtons \left(\text{N}\right).
• Q_1 and Q_2 are the charges in Coulombs \left(\text{C}\right).
• \epsilon_0 is the permittivity of free space, 8.85 \times 10^{-12} \: \text{Fm}^{-1}. This is given on the formula sheet.
• r is the distance between the centre of the two charges in metres \left(\text{m}\right).

When using Coulomb’s Law, we treat air as a vacuum, hence why we use the permittivity of free space \left( \epsilon_0\right). 

Example: Two protons are 2 \: \text{mm} apart. Calculate the electrostatic force of repulsion between the protons given that the charge of a proton is 1.60 \times 10^{-19} \: \text{C}.

[3 marks]

F = \dfrac{Q_1 Q_2}{4 \pi \epsilon_0 r^2}

F = \dfrac{1.6 \times 10^{-19} \times 1.6 \times 10^{-19}}{4 \pi 8.85 \times 10^{-12} \times 0.002^2}

F = 5.75 \times 10^{-23} \: \text{N}

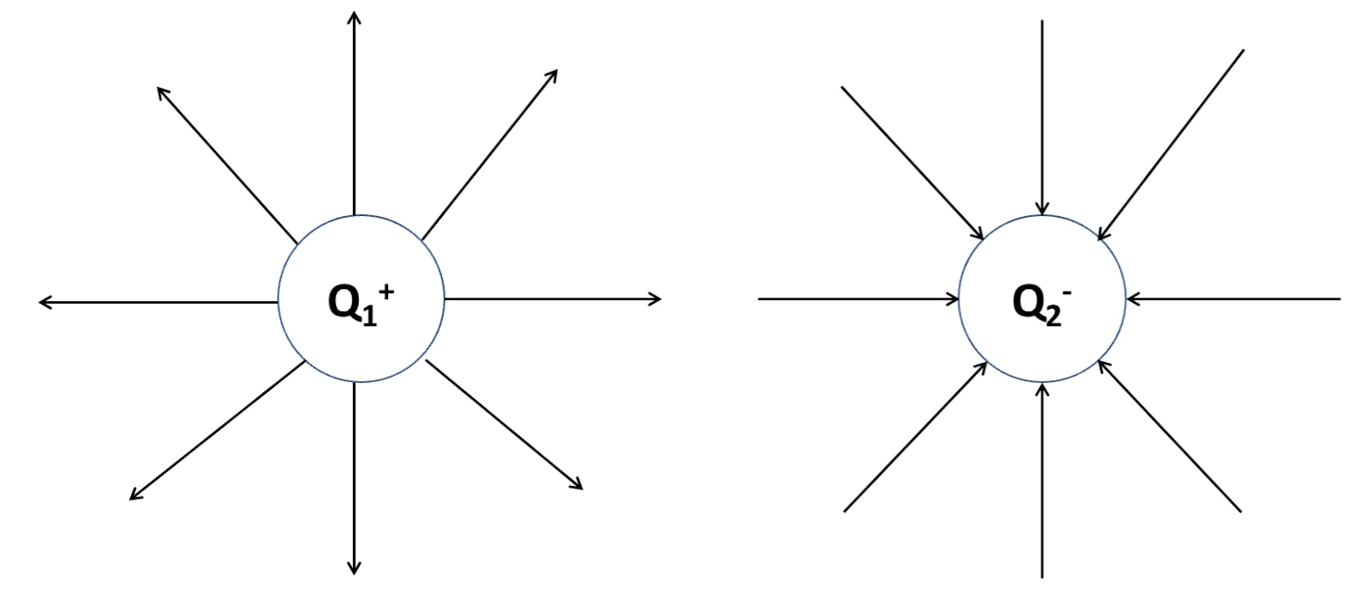
As the field lines are not evenly distributed at all points within the field, radial fields like those above are considered non-uniform.

An example of a uniform electric field can be found between positively charged and negatively charged plates. Remember, the field lines will always flow from positive to negative:

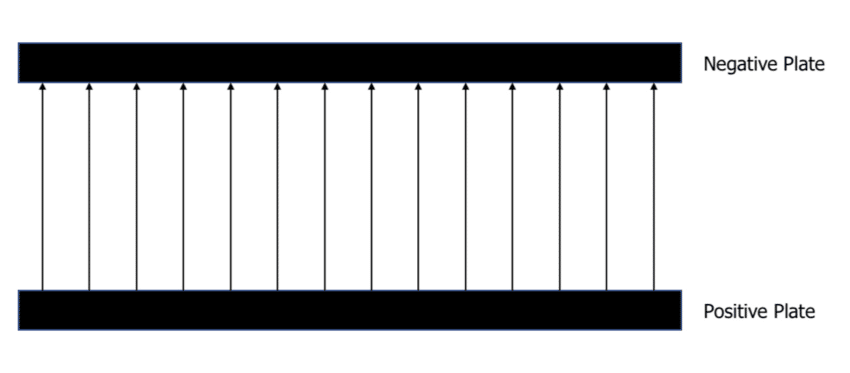
At all points between the plates, the electric field lines are equally spaced. Therefore, the electric field strength is equal at all points.