Electric Field Strength
Electric Field Strength Revision
Electric Field Strength
Previously we have learnt how to calculate the strength of a gravitational field. In this section we look at electric field strength in uniform and radial fields.
Electric Field Strength
Any charged object within an electric field will experience a force acting upon it. If the two charges are oppositely charged , the force will be attractive and if the charges are like, the force will be repulsive.
The electric field strength can be defined as the amount of electrostatic force exerted on an object per unit of charge. In equation form we get:
E = \dfrac{F}{Q}
- E is the electric field strength in volts per metre or Newtons per Coulomb\left(\text{Vm}^{-1} \: \text{or} \: \text{NC}^{-1}\right)
- F is the electrostatic force acting on the charged particle in Newtons \left(\text{N}\right)
- Q is the charge of the object in the field in Coulombs \left(\text{C}\right).
Example: An electron enters an electric field and experiences a force of 0.01 \: \text{N}. Given that the charge of an electron is -1.6 \times 10^{-19} \: \text{C}, calculate the electric field strength of the electric field.
[2 marks]
E = \dfrac{F}{Q}
E = \dfrac{0.01}{-1.6 \times 10^{-19}}
E = \boldsymbol{-6.25 \times 10^{16}} \: \textbf{Vm}^{-1} \: \text{or} \: \textbf{NC}^{-1}
Electric Field Strength in a Uniform Field
When connected to a potential difference, two parallel metal plates become oppositely charged and a uniform electric field forms between them:
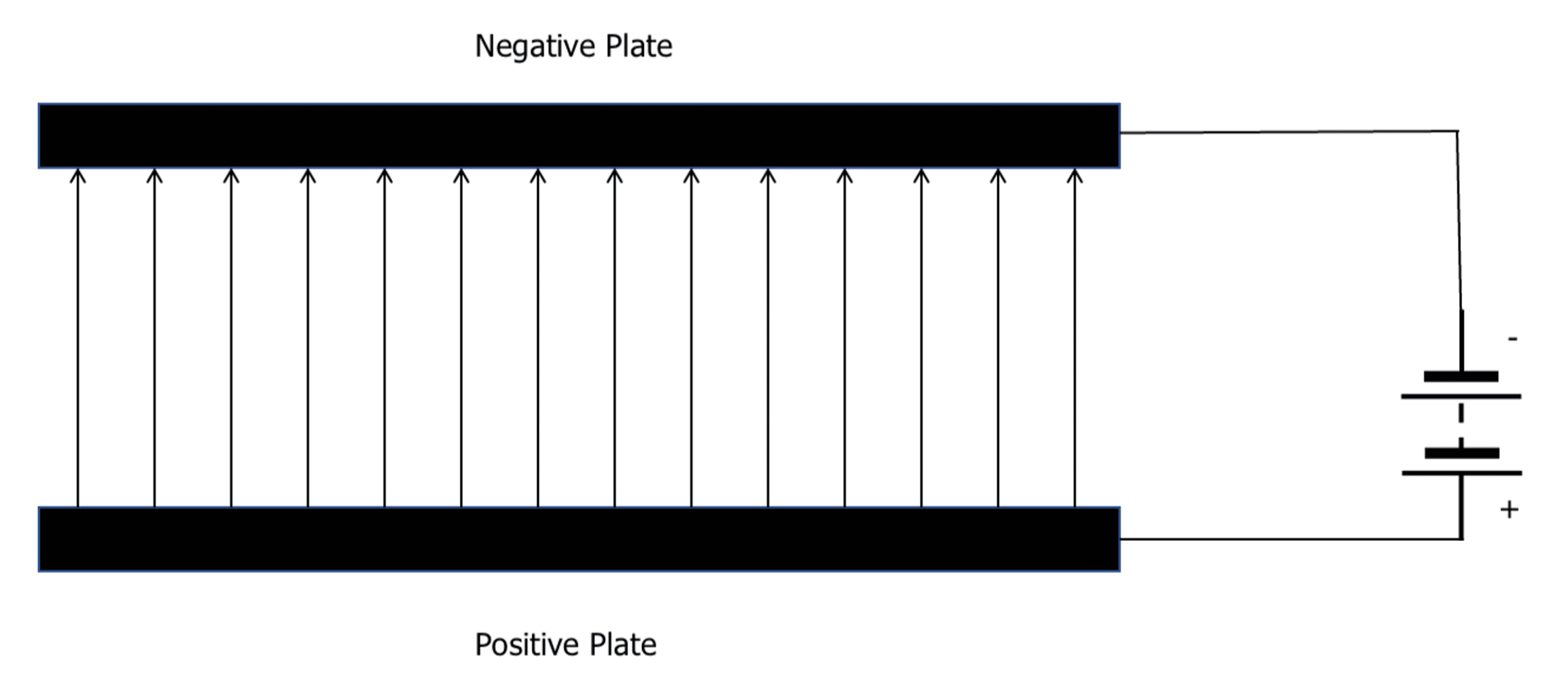
The electric field strength at any point within the field will always be equal, because it is a uniform field.
To calculate the electric field strength between two parallel plates we can use the equation:
E = \dfrac{V}{d}
- E is the electric field strength in volts per metre \left(\text{Vm}^{-1}\right).
- V is the potential difference between the plates in volts \left(\text{V}\right).
- d is the distance between the plates in metres \left(\text{m}\right).
Example: Two parallel plates are connected to a power source providing a d.c supply of 6 \: \text{V}. Calculate the electric field strength when the plates are separated by 0.1 \: \text{m}.
[1 mark]
E = \dfrac{V}{d}
E = \dfrac{6}{0.1}
E = 60 \: \text{Vm}^{-1}
Moving Charges in a Uniform Electric Field
A charged particle has its own electric field. If the charged particle enters a uniform field it will experience a force which will result in a change in direction or velocity. The motion of the charged particle depends upon its mass, charge and velocity.
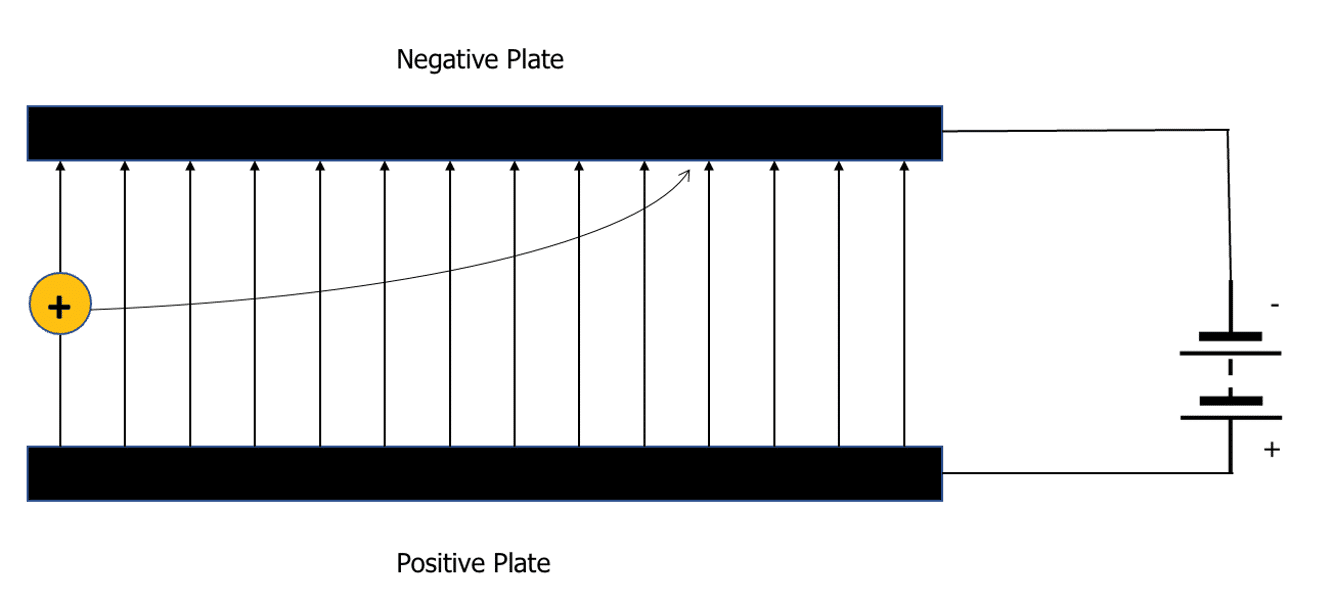
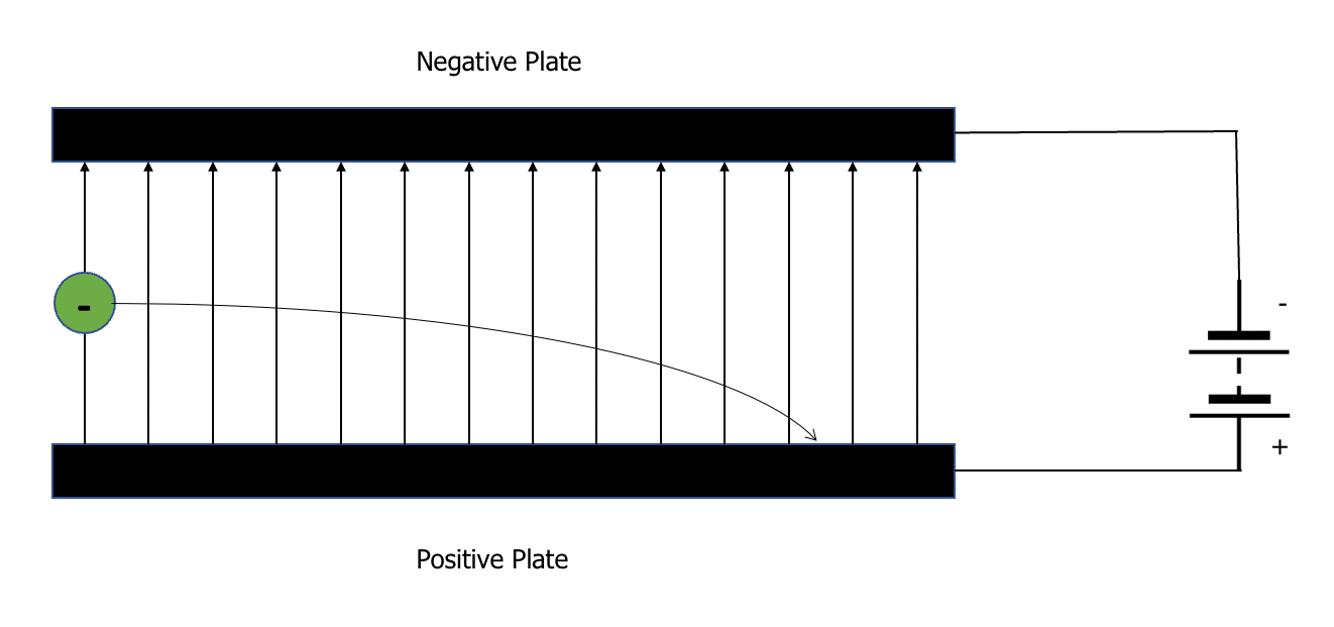
The charged particle will always be attracted to the oppositely charged plate and deflected away from the same charged plate. It will move in a parabola as shown in the diagrams above until it collides with the plate.
To increase the amount of deflection we may:
- Increase the charge.
- Decrease the velocity of the particle.
- Decrease the mass of the particle.
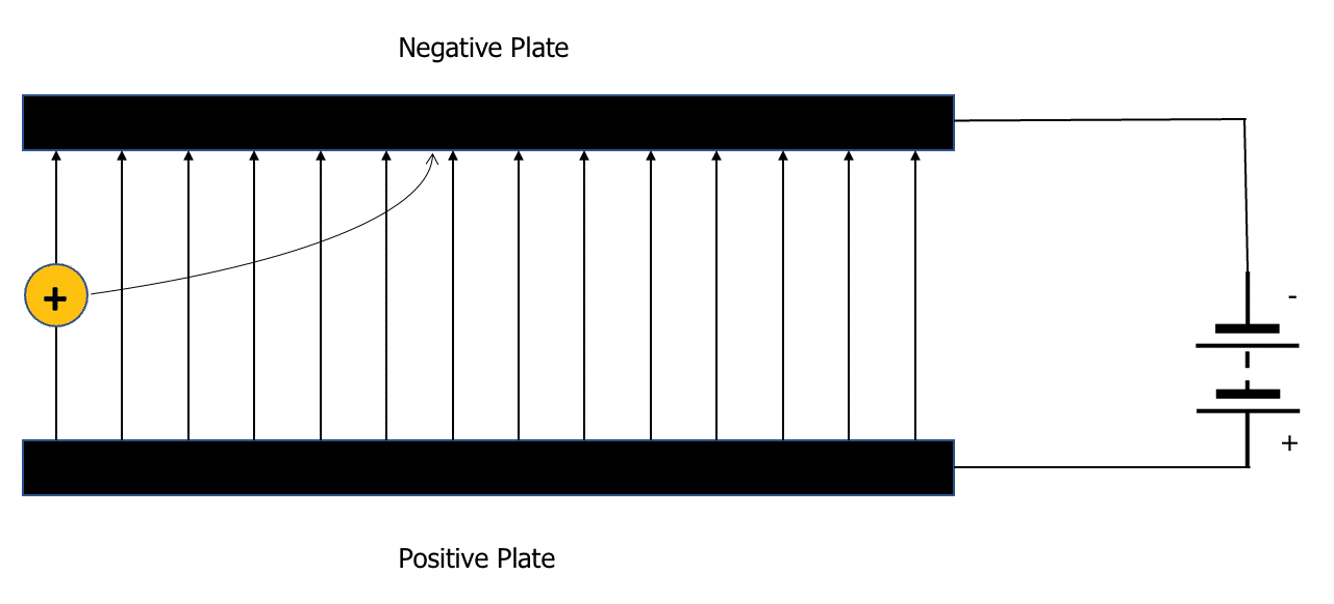
The diagram below shows a proton whose deflection has been increased, as a result of either increased charge, decreased velocity, or decreased mass of the moving charge.
Work done moving a charged particle
If we wanted to know the work done when moving a charge between two parallel plates, we can derive our own equation:
Work done: W = Fd
For a moving charge: F = EQ and d = \dfrac{V}{E}
Substituting F and d into the equation for work done, we arrive at:
W = Q \Delta V
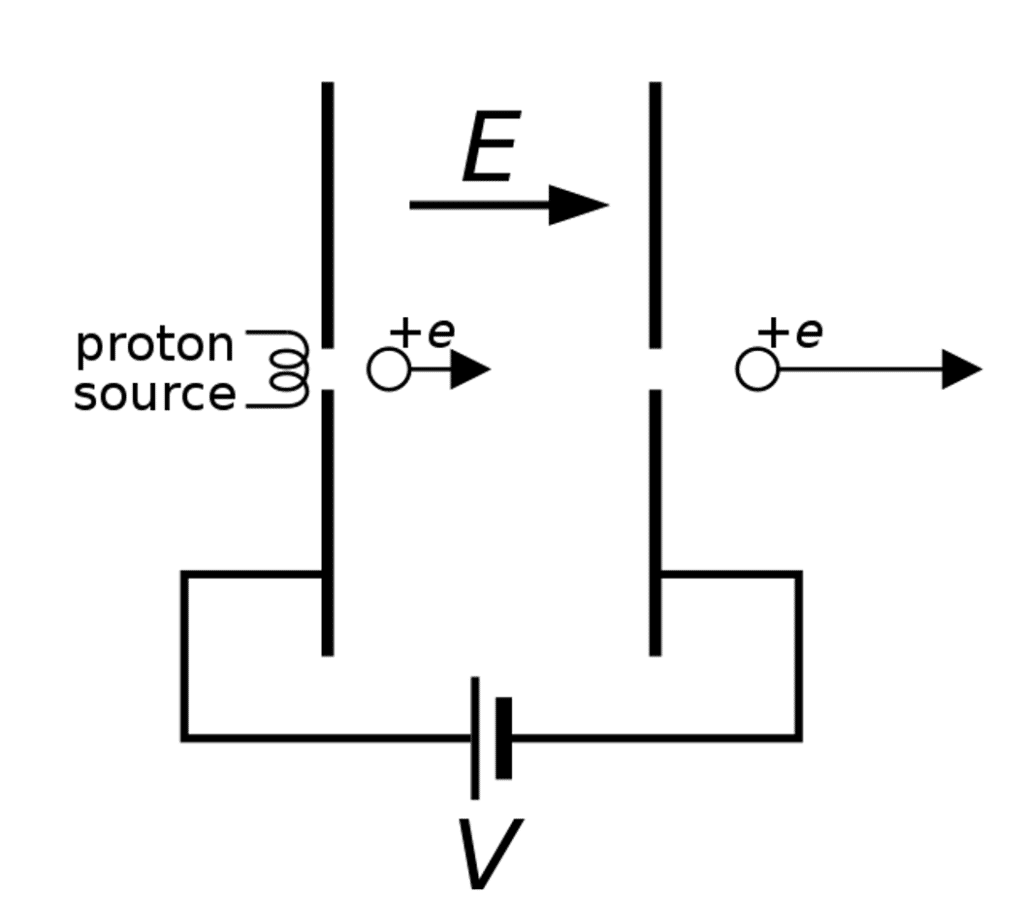

Particle Accelerators
A similar concept can be used for particle accelerators such as the one here.
A proton is fired through a tiny gap in the positively charged plate and towards a negatively charged plate. As the proton is positively charged, it is repelled away from the positive plate and attracted to the negative plate, causing an acceleration. The proton then passes through a tiny gap in the negatively charged plate at a higher velocity than when it entered.
Radial Electric Fields
A point charge produces a radial electric field like the examples below. Remember, the electric field lines point in opposite directions for positive and negative charges:
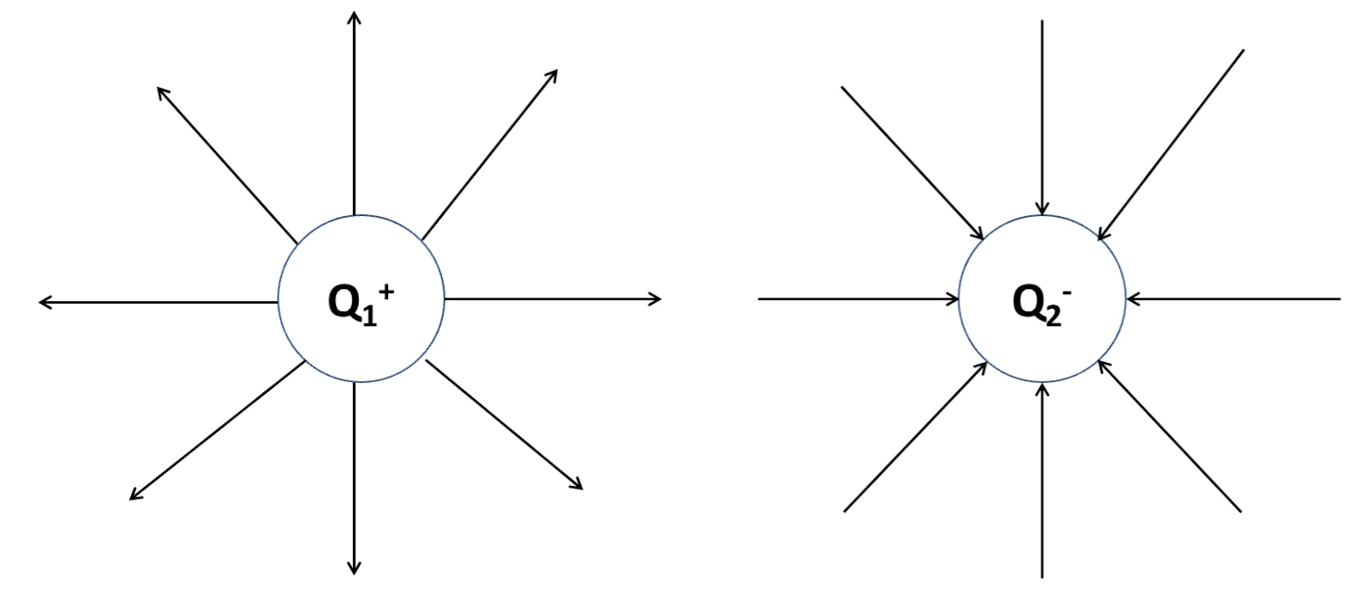
We can see that in the radial electric fields, the field lines get further apart as distance from the particle increases. This represents the changing electric field strength with distance for a radial electric field.
To calculate the electric field strength at any point in the radial electric field, the following equation may be used:
E = \dfrac{Q}{4 \pi \epsilon_0 r^2}
- Q is the charge of the point charge that is causing the field in Coulombs \left(C\right).
- \epsilon_0 is the permittivity of free space, \left(8.85 \times 10^{-12}\right).
- r is the distance from the centre of the charge in metres \left(\text{m}\right).
Example: Calculate the electric field strength at a distance of 0.5 \: \text{mm} away from a proton.
[2 marks]
E = \dfrac{Q}{4 \pi \epsilon_0 r^2}
E = \dfrac{1.6 \times 10^{-19}}{\left(4 \pi \times 8.85 \times 10^{-12} \times \left(0.5 \times 10^{-3}\right)^2\right)}
E = 5.75 \times 10^{-3} \: \text{Vm}^{-1}
Electric Field Strength Example Questions
Question 1: A proton enters an electric field and experiences a force of 0.002 \: \text{N}. Given that the charge of a proton is 1.6 \times 10^{-19} \: \text{C}, calculate the electric field strength.
[2 marks]
Question 2: Describe how a positive point charge would move through a pair of parallel plates with the positively charged plate on the left hand side, and negatively charged plate on the right hand side.
[2 marks]
The point charge will always be attracted to the oppositely charged plate and moves in a parabola. Therefore the positive charge would move to the right towards the negatively charged plate in a parabolic motion.
Question 3: Explain how oppositely charged plates could be used to accelerate a charged particle.
[3 marks]
A proton is fired through a tiny gap in a positively charged plate and towards a negatively charged plate.
As the proton is positively charged, it is repelled away from the positive plate and attracted to the negative plate, causing an acceleration.
The proton then passes through a tiny gap in the negatively charged plate at a higher velocity than when it entered.
This would also work for an electron but the polarity of the plates would need to be reversed.
Question 4: Calculate the electric field strength at a distance of 0.12 \: \text{mm} away from an electron.
[2 marks]
Electric Field Strength Worksheet and Example Questions
Electric Field Questions
A LevelOfficial MMEYou May Also Like...

MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.