Electric Potential
Electric Potential Revision
Electric Potential
Just like in a gravitational field, moving a charge in an electric field changes the amount of electric potential energy the charge has. In this section we look at the idea of electric potential and calculate the work done moving a charged particle in an electric field.
Electric Potential
To move like charges together, or opposite charges further apart, work must be done. This is because we are moving the charges in the opposite direction to overcome the electrostatic forces of attraction or repulsion. In doing so, the potential energy of the charge being moved is increased.

As seen above, the electrostatic force for two like charges is repulsive. Therefore, moving the like charges together requires work to be done and increases the electric potential. Likewise, if a pair of opposite charges are separated against their attractive electrostatic force, work is done and the electric potential increases.
In both cases, at infinity (a point outside the electric field of both point charges) the electric potential is zero.
The electric potential can therefore be defined as the work done per unit of charge in moving a charge from infinity to a specific point within the electric field of the charge.
Electric Potential at a specific point can be calculated using the equation:
V = \dfrac{Q}{4 \pi \epsilon_0 r}
- V is the electric potential at the point you are calculating in volts \left(\text{V}\right).
- Q is the charge of the point charge causing the electric field in Coulombs \left(\text{C}\right).
- \epsilon_0 is the permittivity of free space \left(8.85 \times 10^{-12} \: \text{Fm}^{-1}\right).
- r is the distance from the centre of the point charge in metres \left(\text{m}\right).
Example: A Van de Graaf generator has a charge of 5.0 \times 10^{-6} \: \text{C}. Calculate the electric potential at a distance of 0.5 \: \text{m} away from the centre of the generator.
[2 marks]
V = \dfrac{Q}{4 \pi \epsilon_0 r}
V = \dfrac{5 \times 10^{-6}}{\left(4 \pi \times 8.85 \times 10^{-12} \times 0.5 \right)}
V = 90000 \: \text{V} \: \text{or} \: 90 \: \text{kV}
Electric Potential Difference
As with Gravitational Potential, we can calculate the electrical potential difference between two points in an electric field. This is known as the electrical potential difference \left( \Delta V \right).
\Delta V = V_f – V_i
where V_f is the final electric potential and V_i is the initial electric potential, both in joules per coulomb \left(\text{JC}^{-1}\right).
Example: An electron is moved from a point in an electric field where the electric potential is +1.9 \: \text{JC}^{-1} to another point where the electric potential is +0.2 \: \text{JC}^{-1} . Calculate the potential difference between the two points in the electric field.
[1 mark]
\Delta V = V_f - V_i
\Delta V = 0.2 - 1.9
\Delta V = -1.7 \: \text{JC}^{-1}
Work Done on a Charged Particle
Work needs to be done to move a charge through an electric field. As the charge moves though the field, it’s electric potential is changing. This is described by the following equation:
\Delta W = q \Delta V
- \Delta W is the change in work done in joules \left(\text{J}\right).
- q is the charge of the moving charged particle in Coulombs \left(\text{C}\right).
- \Delta V is the change in electric potential in volts \left(\text{V}\right).
Therefore we can see that the change in work done is equal to the change in electric potential energy.
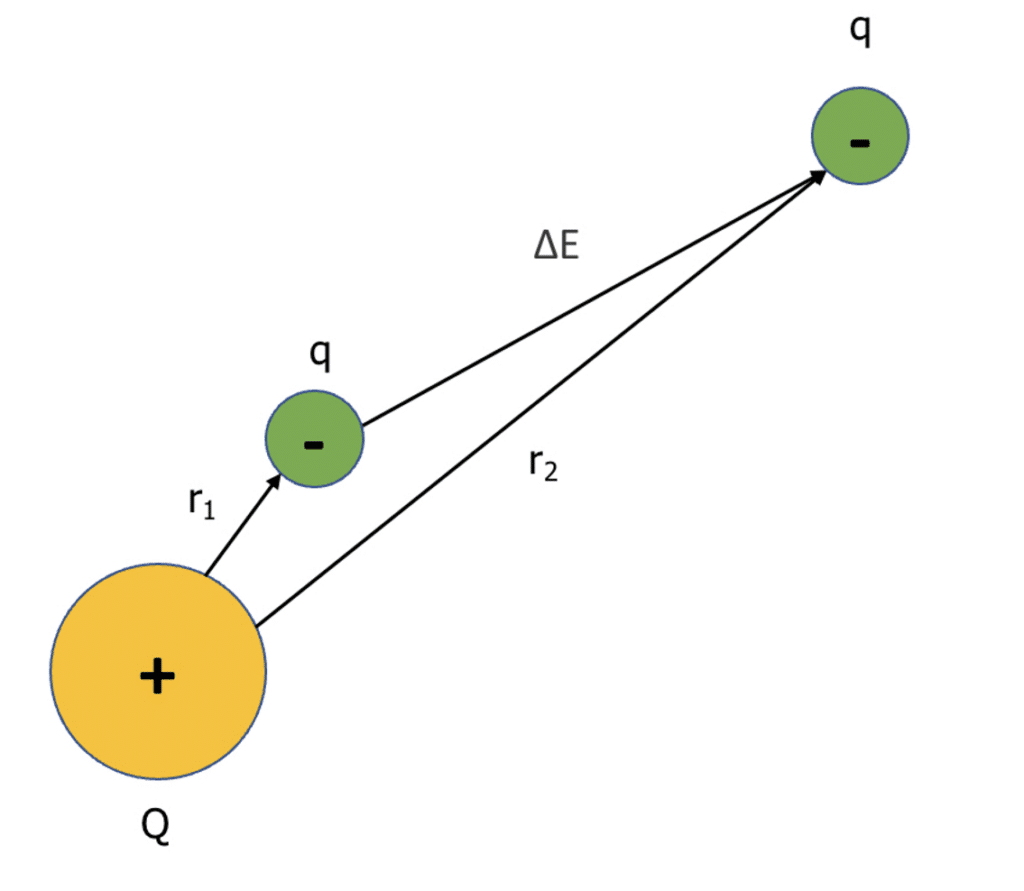

Change in electric potential energy can be calculated using the following equation:
\text{Change in electric potential energy} = \dfrac{Qq}{4 \pi \epsilon_0 \Delta r}
where Q is the point charge, q is the moving charge, \epsilon_0 is the permittivity of free space \left(8.85 \times 10^{-12}\right) and \Delta r is the change in distance from the centre of the charge \left(r_2 – r_1\right).
In the above example, the change in electric potential energy and the work done are positive as we are moving against the electrostatic attraction so we need to do work. If the moving charge was moving towards the point charge, the work done would be negative.
If a moving charge moves perpendicular to the field lines, no work is done as there would be no \Delta r and therefore no change in electric potential.
Electric Potential Example Questions
Question 1: A positive charge is moved away from a negative charge. Describe why the moving charge gains electric potential.
[2 marks]
As the electrostatic force between opposite charges is attractive, moving the charges apart requires work to be done and therefore, electric potential increases.
Question 2: Calculate the electric potential at a distance of 0.1 \: \text{m} away from the centre of a point charge of 1 \times 10^{-7} \: \text{C}.
[2 marks]
Question 3: An alpha particle is moved from a point in an electric field where the electric potential is +0.9 \: \text{JC}^{-1} to another point where the electric potential is +2.2 \: \text{JC}^{-1} . Calculate the potential difference between the two points in the electric field.
[1 mark]
You May Also Like...

MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.