Quadratic Graphs

A LevelAQAEdexcelOCR

Quadratic Graphs Revision

Quadratic Graphs

You will need to be able to identify and sketch quadratic graphs.

Make sure you are happy with the following topics before continuing.

Solving Quadratic Equations

Quadratic Graph Shapes

Quadratic graphs have the general form

$\textcolor{red}{a} x^2 + \textcolor{blue}{b}x + \textcolor{limegreen}{c}$

These can be either u-shaped (if $\textcolor{red}{a}$ is positive) or n-shaped (if $\textcolor{red}{a}$ is negative)

Some examples of quadratic graphs can bee seen below:

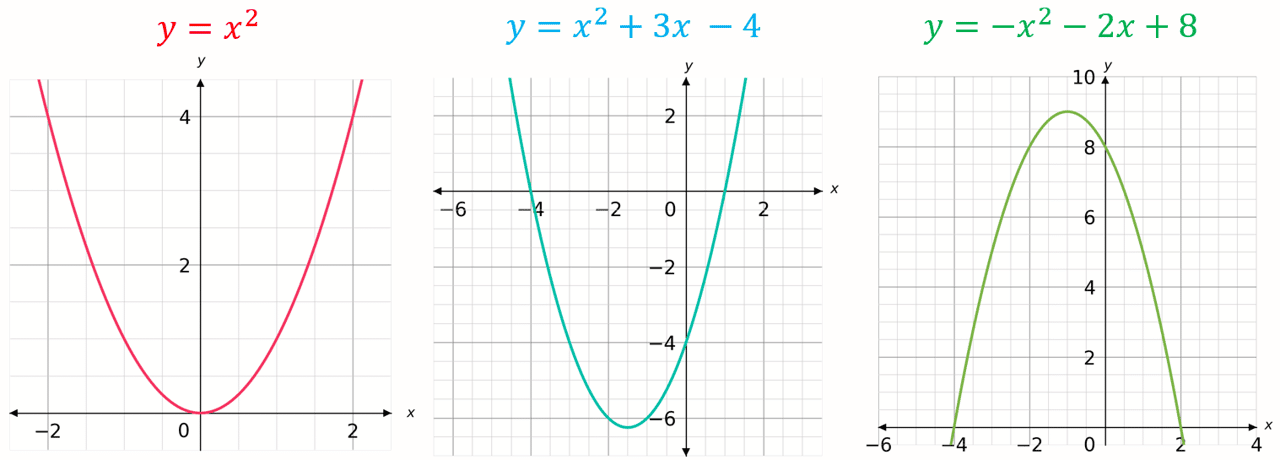
Sketching Quadratic Graphs

To sketch quadratic graphs, you need to follow these steps:

Step 1: Decide whether the graph is an n-shape or a u-shape.

u-shaped if the coefficient of $x^2$ is positive
n-shaped if the coefficient of $x^2$ is negative

Step 2: Find the intersections with the $x$ -axis (set $y=0$ ) and $y$ -axis (set $x=0$ )

Step 3: Find the maximum (if it is an n-shaped graph) or minimum (if it is a u-shaped graph) using symmetry or completing the square.

Step 4: Sketch the graph and label all the important points.

Example: Sketch the graph of $y = 2x^2 + 3x - 2$

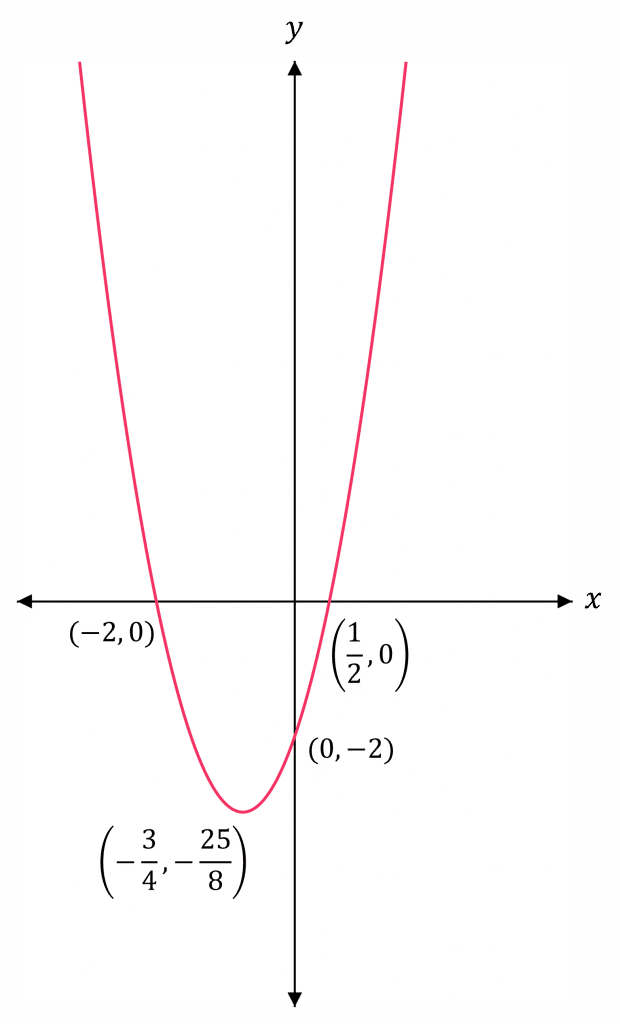
Step 1: The coefficient of $x^2$ is positive, so the graph is u-shaped.

Step 2: When $y=0$ ,

$\begin{aligned} 2x^2 + 3x - 2 &= 0 \\ (2x-1)(x+2) &= 0 \end{aligned}$

$x = \dfrac{1}{2}$ or $x = -2$

Hence, the curve crosses the $x$ -axis at $\textcolor{red}{\left( \dfrac{1}{2}, 0 \right)}$ and $\textcolor{red}{(-2,0)}$

When $x = 0$ ,

$y = 2(0)^2 + 3(0) - 2 = -2$

Hence, the curve crosses the $y$ -axis at $\textcolor{red}{(0,-2)}$

Note: You can often read off the value the graph crosses the $y$ -axis at (called the $y$ -intercept) from the equation of a quadratic. The $y$ -intercept of $y=ax^{2}+bx+c$ is always $c$ .

Step 3: The minimum value will be halfway between $\left(\dfrac{1}{2}, 0 \right)$ and $(-2,0)$ :

$\left( \dfrac{1}{2} - 2 \right) \div 2 = - \dfrac{3}{4}$

So, the minimum value is at $x = - \dfrac{3}{4}$

Therefore, the minimum is

$y = 2 \left(- \dfrac{3}{4} \right)^2 + 3 \left(- \dfrac{3}{4} \right) - 2 = - \dfrac{25}{8}$

So, the graph has a minimum at the point $\textcolor{red}{\left(- \dfrac{3}{4}, - \dfrac{25}{8} \right)}$

Step 4: Sketch the graph (sketching doesn’t need to be to scale) and label all the important points.

Completing the Square to Sketch Graphs

You can complete the square to help sketch quadratic curves.

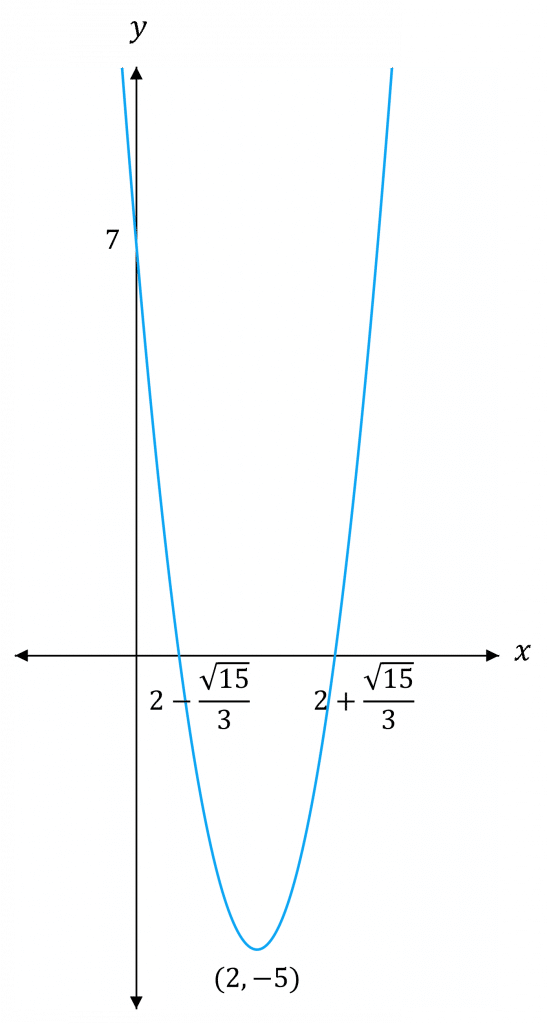
Example: Sketch the curve of $y = 3x^2 - 12x + 7$

Firstly, complete the square:

$y = 3x^2 - 12x + 7 = 3(x-2)^2 - 5$

When $y=0$ ,

$\begin{aligned} 3(x-2)^2 - 5 &=0 \\ (x-2)^2 &= \dfrac{5}{3} \\ x - 2 &= \pm \sqrt{\dfrac{5}{3}} \\ x &= 2 \pm \dfrac{\sqrt{15}}{3} \end{aligned}$

So, the curve crosses the $x$ -axis at $\textcolor{red}{\left(2-\dfrac{\sqrt{15}}{3},0 \right)}$ and $\textcolor{red}{\left(2+\dfrac{\sqrt{15}}{3},0 \right)}$

When $x=0$ ,

$y = 3(0)^2 - 12(0) + 7 = 7$

So, the curve crosses the $y$ -axis at $\textcolor{red}{(0,7)}$

$(x-2)^2 \geq 0$ (since a square number is never less than $0$ ), therefore the minimum value occurs at $x-2=0 \Rightarrow x = 2$ , and therefore the minimum is

$y = 3(2-2)^2 - 5$

So, the minimum is at the point $\textcolor{red}{(2, -5)}$

Then, you have enough information to sketch the graph.

Note: You can read off the vertex of a graph from completed square form. The vertex of $y=a(x+b)^{2}+c$ is always at $(-b,c)$ .

Functions with no Real Roots

Some functions have no real roots – i.e. its graph doesn’t cross the $x$ -axis. You can complete the square and use this to see if quadratics have real roots, or not.

Example: $f(x) = x^2 + 2x + 6$ . Determine whether $f(x)$ has any real roots.

Complete the square:

$f(x) = x^2 + 2x + 6 = \textcolor{red}{(x+1)^2} + \textcolor{blue}{5}$

$\textcolor{red}{(x+1)^2}$ is never less than $0$ , therefore the minimum of the curve of $f(x)$ is at $\textcolor{blue}{5}$ .

Hence, $f(x)$ cannot be negative and will not cross the $x$ -axis at any point.

Therefore, $f(x)$ has no real roots.

Note: If the coefficient of $x^2$ is negative, you can do a similar thing to see if $f(x)$ has real roots, by checking if $f(x)$ is ever positive.

Quadratic Graphs Example Questions

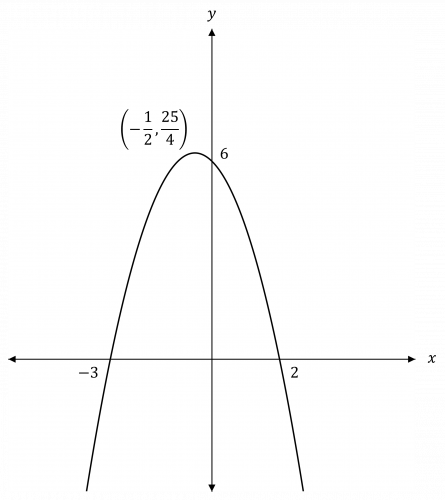
Question 1: Sketch the graph of $y = 6 - x - x^2$ .

[4 marks]

The coefficient of $x^2$ is negative, so the graph is n-shaped.

When $x = 0$ , $y = 6$

When $y = 0$ ,

$\begin{aligned} 6 - x - x^2 &= 0 \\ (2-x)(x+3) &= 0 \end{aligned}$

$x = 2$ or $x = -3$

The maximum value is halfway between $-3$ and $2$ . So the maximum is at $x = - \dfrac{1}{2}$ and $y = 6 - \left(- \dfrac{1}{2} \right) - \left(- \dfrac{1}{2} \right)^2 = \dfrac{25}{4}$

So, we have enough information to plot the graph: