The Quadratic Formula

The Quadratic Formula is used to find the solutions to any quadratic equation.

The following topics are referred to in this page.

Inequalities

The Quadratic Formula

The solutions to the quadratic equation

$\textcolor{red}{a} x^2 + \textcolor{blue}{b}x + \textcolor{limegreen}{c} = 0$

are given by the quadratic formula:

$x=\dfrac{-\textcolor{blue}{b}\pm\sqrt{\textcolor{blue}{b}^2-4\textcolor{red}{a}\textcolor{limegreen}{c}}}{2\textcolor{red}{a}}$

Note: There are two solutions for $x$ : one using $+$ and the other using $-$

The Discriminant

The discriminant of the quadratic formula (written as $D$ or $\Delta$ ) is the part under the square root sign. i.e. the discriminant is

$b^2-4ac$

It can be positive, zero or negative – these tell us how many roots the quadratic equation has:

If $b^2 - 4ac > 0$ , then the quadratic has $2$ real roots (that are distinct)
If $b^2 - 4ac = 0$ , then the quadratic has $1$ real root (or ‘equal roots’)
If $b^2 - 4ac < 0$ , then the quadratic has no real roots

This can be seen visually:

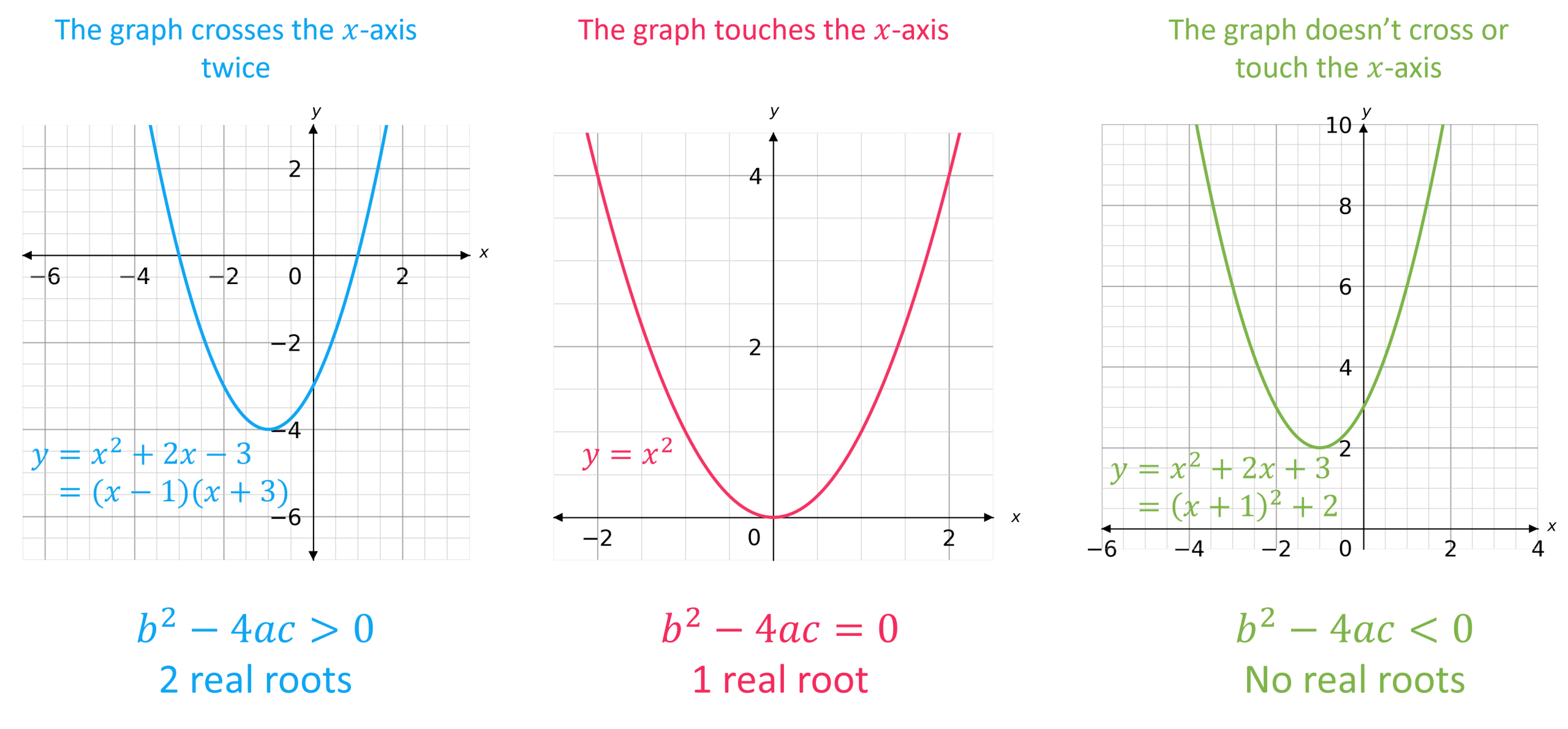
Note: We say no ‘real’ roots since some quadratics can have ‘imaginary’ roots – however we will not see this in this course.

Example 1: Using the Quadratic Formula

Find the solutions to the quadratic equation $3x^2 - 8x + 2=0$ , giving your answers in surd form.

[2 marks]

$a = 3$ , $b = -8$ and $c = 2$

Put these values into the quadratic formula:

$\begin{aligned} x &= \dfrac{-(-8) \pm \sqrt{(-8)^2 - 4 \times 3 \times 2}}{2 \times 3} \\ &= \dfrac{8 \pm \sqrt{40}}{6} \\ &= \dfrac{4 \pm \sqrt{10}}{3} \end{aligned}$

So, $x = \textcolor{orange}{\dfrac{4 + \sqrt{10}}{3}}$ or $\textcolor{orange}{x = \dfrac{4 - \sqrt{10}}{3}}$

Example 2: Finding the Discriminant

How many real roots does the quadratic equation $2x^2 - 5x + 3=0$ have?

[2 marks]

$a = 2$ , $b = -5$ and $c = 3$

So, the discriminant is

$b^2-4ac = (-5)^2 - 4 \times 2 \times 3 = 1$

The discriminant is $>0$ , so $2x^2 - 5x + 3=0$ has two real roots.

Example 3: Using the Discriminant

$f(x) = 2x^2 + 4x + k$ . Find the values of $k$ for which $f(x)=0$ has no real roots.

[3 marks]

$a = 2$ , $b = 4$ and $c = k$

The discriminant is

$b^2 - 4ac = 4^2 - 4 \times 2 \times k = 16 - 8k$

The quadratic equation has no real roots, therefore $b^2 - 4ac < 0$

So,

$\begin{aligned} 16 - 8k &< 0 \\ 16 &< 8k \\ \textcolor{orange}{k} &\textcolor{orange}{> 2} \end{aligned}$

Example 4: Using the Discriminant

$kx^2 + 2kx + 3 = 0$ has two distinct real roots.

Find the set of values for which $k$ satisfies this.

[5 marks]

$a = k$ , $b = 2k$ and $c = 3$

The discriminant is

$b^2 - 4ac = (2k)^2 - (4 \times k \times 3) = 4k^2 - 12k$

Since the quadratic equation has two distinct real roots, the discriminant must be $>0$

$4k^2 - 12k > 0$

The quadratic can be factorised:

$4k^2 - 12k = 4k(k-3)$

This is $0$ when $k=0$ or when $k=3$

Hence, $4k(k-3)>0$ when $\textcolor{orange}{k<0}$ or when $\textcolor{orange}{k>3}$

Note: You can draw a graph of $y = 4k(k-3)$ to help – you would see a u-shaped graph that crosses the $k$ -axis at $0$ and $3$ (see inequalities).

The Quadratic Formula Example Questions

Question 1: Solve $2x^2 - 4x = 1$ , giving your answers to $2$ decimal places.

[2 marks]

Rearrange the equation so that it is in the form $ax^2 + bx + c = 0$ :

$2x^2 - 4x - 1 = 0$

Then, $a = 2$ , $b = -4$ and $c = -1$

Put these values into the quadratic formula:

$\begin{aligned} x &= \dfrac{-(-4) \pm \sqrt{(-4)^2 - 4 \times 2 \times -1}}{2 \times 2} \\ &= \dfrac{4 \pm \sqrt{24}}{4} \\ &= \dfrac{2 \pm \sqrt{6}}{2} \end{aligned}$

So,

$x = \dfrac{2 + \sqrt{6}}{2} = 2.22 \text{ (2 dp)}$

$x = \dfrac{2 - \sqrt{6}}{2} = -0.22 \text{ (2 dp)}$